Курсач. приписка. Курсовая работа по дисциплине Введение в информационные технологии
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
2.2)Представление результатов в виде графиков. Построение линии тренда.Результаты построения линии тренда представлены на рисунках 5, 6, 7. 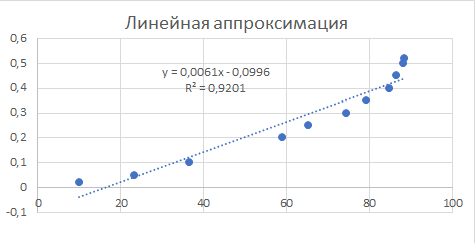 Рис. 5. Исходные точки и линия тренда для линейной аппроксимации.  Рис. 6. Исходные точки и линия тренда для квадратичной аппроксимации. 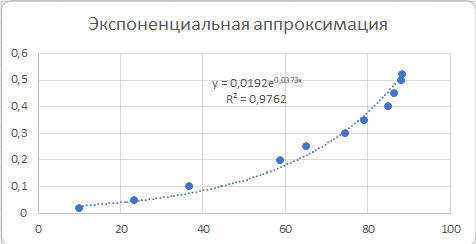 Рис. 7. Исходные точки и линия тренда для экспоненциальной аппроксимации. Сравнивая данные результаты с результатами, полученными ранее вручную с использованием основных расчётных формул, видим, что они полностью совпадают. Это указывает на то, что вычисления верны. 2.3)Получение числовых характеристик с использованием функции ЛИНЕЙН и ЛГРФПРИБЛРезультаты расчётов числовых характеристик представлены на рисунках 8,9,10. 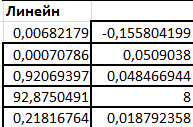 Рис. 8. – Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН для линейной аппроксимации Здесь в интервале ячеек G20:Н24 введена формула =ЛИНЕЙН(А4:А13;В4:В13;;ИСТИНА). В ячейках E26 и E27 расположены соответственно значения коэффициентов  и и 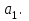 В ячейках G21:Н21 расположены соответственно значения стандартных ошибок коэффициентов  и и 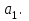 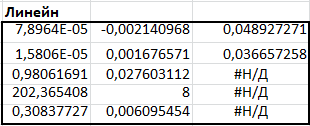 Рис.9. Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН для квадратичной аппроксимации Здесь в интервале ячеек G37:I41 введена формула =ЛИНЕЙН(A3:A13;B3:C13;;ИСТИНА). В ячейках G35, H35 и I35 расположены соответственно значения коэффициентов 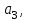  и и 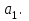 В ячейках F40, F41 и F42 расположены соответственно значения стандартных ошибок коэффициента 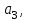  и и 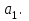 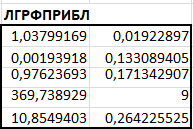 Рис.10. Фрагмент рабочего стола MS Excel использование функции ЛГРФПРИБЛ для экспоненциальной аппроксимации Здесь в интервал ячеек G52:H56 введена формула =ЛГРФПРИБЛ(A3:A13;B3:B13;;ИСТИНА). В ячейке E56 расположено значения коэффициента 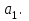 Сравнивая результаты, полученные с помощью функции ЛИНЕЙН и ЛГРФПРИБЛ, с результатами полученными вручную с использованием основных расчётов формул, можно видеть , что они полностью совпадают. Это указывает на то, что вычисления верны. Лучше всего результаты испытаний, аппроксимирует квадратичная функция y = 8E-05x2 - 0,0021x + 0,0489 т.к коэффициент детерминированности квадратичной аппроксимации выше. Полученное соотношение является простым и пригодным для анализа и прогноза, Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности. 2.4)Вычисление прогнозного значенияПрогноз значение давления взрыва при заданной концентрации пыли вычисляем с помощью функции наиболее хорошо аппроксимирующей табличные данные. Результаты вычислений прогнозного значения представлены на рисунке 11. 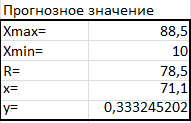 Рис.11. Фрагмент рабочего листа MS Excel вычисления прогнозного значения Здесь в ячейку Н29 введена формула =МАКС(B3:B16). В ячейку Н30 введена формула =МИН(B3:B16). В ячейку Н31 введена формула =H29-H30. В ячейку Н32 введена формула =B20+0,1*H31. В ячейку Н31 введена формула =E26+E27*H32. |
