Курсач. приписка. Курсовая работа по дисциплине Введение в информационные технологии
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
ВведениеЦель данной курсовой работы — с помощью аппроксимации установить зависимость между экспериментальными данными, решить поставленную задачу различными способами, провести расчеты с помощью табличного процессора Microsoft Excel и среды программирования VBA. Аппроксимация - приближенное описание эмпирических данных с помощью уравнений, необходима для проведения интер- и экстраполяции. Задача – найти такую функцию, выраженную аналитической формулой, чтобы она наилучшим образом описывала эмпирические данные. Наиболее часто используется метод наименьших квадратов, который позволяет найти функцию с такими параметрами, что сумма квадратов отклонений найденной функции от заданных значений функции будет минимальной. Между величинами может существовать точная связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При ведении научных исследований, обработке результатов наблюдения или эксперимента обычно приходиться сталкиваться со вторым вариантом. При выполнении любой научно-исследовательской работы возникает проблема выявления подлинного характера зависимости изучаемых показателей. Для этого и применяется аппроксимация ― приближенное описание корреляционной зависимости переменных подходящим уравнением функциональной зависимости, передающим основную тенденцию зависимости (или ее "тренд"). При выборе аппроксимации следует исходить из конкретной задачи исследования. Важно учитывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, многопараметрическое уравнение. Таким образом, выбирая метод аппроксимации, исследователь всегда идет на компромисс: решает, в какой степени в данном случае целесообразно и уместно «пожертвовать» деталями и, соответственно, насколько обобщенно следует выразить зависимость сопоставляемых переменных. Специалисты в области автоматизации технологических процессов и производств имеют дело с большим объёмом экспериментальных данных, для обработки которых используется компьютер. При рассмотрении различных задач в этой области возникает, в частности, необходимость выявления некоторых эмпирических закономерностей, решения систем уравнений, первичной статистической обработки экспериментальных данных. Для решения многих задач, исходные данные и полученные результаты вычислений которых могут быть представлены в табличной форме, используют табличные процессоры (электронные таблицы) и, в частности, Ехсеl. Имеется также множество инженерных задач, для решения которых требуется применить язык программирования. В данной работе использована среда языка программирования VBA для основной массы расчетов, то есть для нахождения зависимости температуры продуктов взрыва от дисперсности наполнителей в составе взрывчатых веществ, электронные таблицы Microsoft Excel из пакета Microsoft Office для создания контрольного варианта и построения графиков; текстовой редактор Microsoft Word для оформления отчета о проделанной работе. При выполнении работы были использованы материалы лекций и рекомендованные источники литературы. 1)Расчётные формулыЕсть разные способы оценки суммарной ошибки аппроксимации, Чаще всего оценивают суммарную квадратичную ошибку, равную сумме квадратов отклонений эмпирических значений функции от теоретических: Эмпирическая формула: 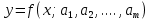 (1) (1)Где  - неизвестные параметры, значения которой в точка - неизвестные параметры, значения которой в точка 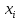 мало отличались бы от опытных значений мало отличались бы от опытных значений 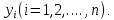 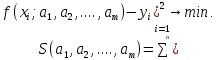 (2) (2)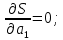 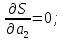  (3) (3)Нахождения коэффициента 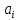 сводиться к решению системы (3). сводиться к решению системы (3).В случае линейной формулы зависимости 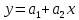 система (3) примет вид: система (3) примет вид: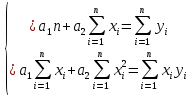 (4) (4)В случаи квадратичной зависимости  система (3) примет вид: система (3) примет вид: (5) (5)Экспоненциальная зависимость: 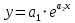 (6) (6)Где 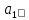 и и 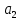 - неопределённые коэффициенты. - неопределённые коэффициенты.Линеаризация достигается путём логарифмирования равенства (6), после чего получим соотношение. 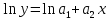 (7) (7)Коэффициент корреляции вычисляется по формуле: 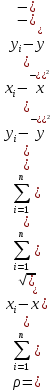 (8) (8)Где 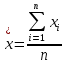 , , 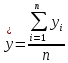 , , 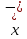 и и 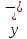 - среднее арифметическое значения соответственно по x и y. - среднее арифметическое значения соответственно по x и y.Коэффициент детерминированности (детерминации) определяться по формуле:  (9) (9)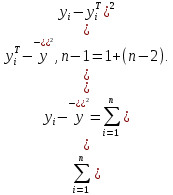 (10) (10)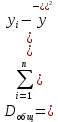 (11) (11) ; (12) ; (12)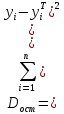 , (13) , (13)Где m- число параметров при переменных x. Для линейной и экспоненциальной аппроксимации m=1, для квадратичной аппроксимации m=2. Критерий Фишера определяться соотношение:  (14) (14)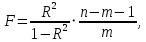 (15) (15)Для линейной и экспоненциальной функции формула имеет вид: 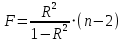 . (16) . (16)Для параболы формула F- критерия будет: 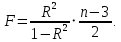 (17) (17)Стандартная ошибка коэффициента регрессии 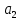 определяется по формуле: определяется по формуле: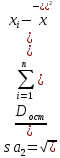 . (18) . (18) Стандартная ошибка параметра 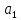 : :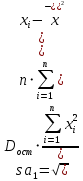 . (19) . (19)Для оценки значимости квадратичной зависимости используется аналогичный подход. Значения стандартных ошибок вычисляются по формулам:  (20) (20)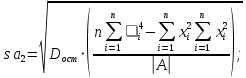 (21) (21)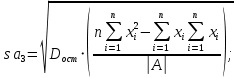 (22) (22)где |A| - определитель матрицы  . . |
