взаимозаменяемость. Курсовая взаимозаменяемость. Курсовая работа по дисциплине Взаимозаменяемость
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
3. Выбор посадок гладких цилиндрических соединений3.1 Выбор переходной посадкиДля переходной посадки, указанной на схеме, определим номинальный диаметр, замерив его на сборочном чертеже и округлив до ближайшего значения из ряда [2]. Радиальное биение и коэффициент запаса точности выберем из задания по своему варианту. Дано: номинальный размер Ø 45; радиальное биение Fr =40 мкм; коэффициент запаса точности KT = 2,0. Для обеспечения заданного радиального биения максимальный зазор Smax в переходной посадке не должен превышать Smax = 40/2 = 20 мкм. В рассматриваемом примере примем систему вала. Примем поле допуска основного вала 45h5 и по таблицам стандартов [2] определим цифровые значения предельных отклонений: верхнее es = 0; нижнее ei = -11 мкм. Для того, чтобы максимальный зазор не превышал 20 мкм верхнее отклонение отверстия ЕS не должно быть больше 9 мкм ( 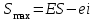 ). Ближайшим полем допуска отверстия является 45 К5 c предельными отклонениями: ЕS = 2 мкм; ЕI= -9 мкм. Для выбранной переходной посадки построим схему расположения полей допусков (рис. 3.1) и определим: ). Ближайшим полем допуска отверстия является 45 К5 c предельными отклонениями: ЕS = 2 мкм; ЕI= -9 мкм. Для выбранной переходной посадки построим схему расположения полей допусков (рис. 3.1) и определим:наибольший предельный размер отверстия Dнб = 45,002 мм; наименьший предельный размер отверстия Dнм = 44,991 мм; наибольший предельный размер вала dнб = 45,000 мм; наименьший предельный размер вала dнм = 45,989 мм; допуск отверстия TD = 11 мкм; допуск вала Td = 11 мкм; наибольший зазор Smax= 13 мкм; наибольший натяг Nmax = 2 мкм; средний зазор Sср = 2 мкм, который соответствует средним размерам деталей и определяется по формуле: 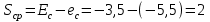 где 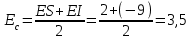 - серединное отклонение отверстия; - серединное отклонение отверстия;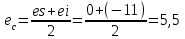 - серединное отклонение вала. - серединное отклонение вала.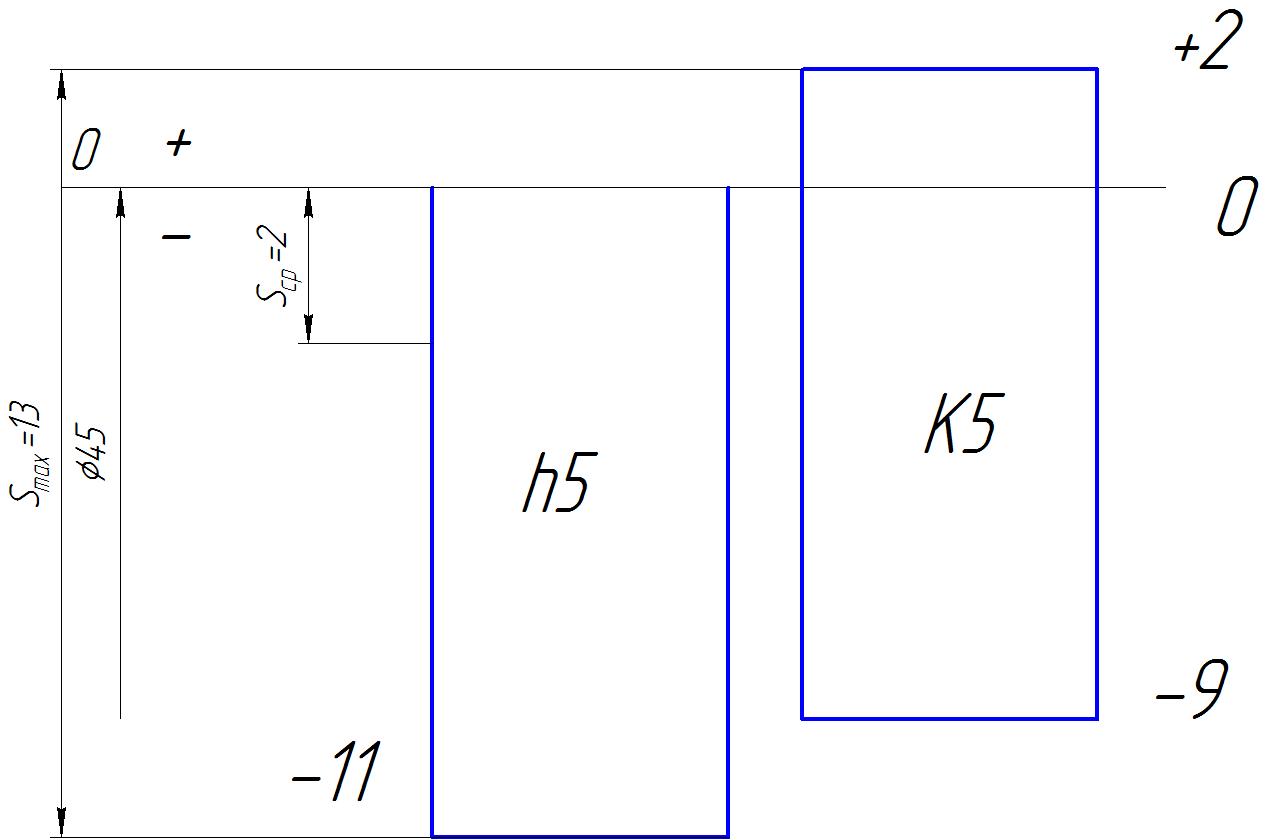 Рисунок 3.1. Схема расположения полей допусков переходной посадки Определим вероятность получения в данной посадке зазоров и натягов, считая, что рассеяние размеров подчиняется нормальному закону, который описывается кривой Гаусса (рис. 3.2). На расстоянии х = Sср = 2 мкм от оси у находится ордината, соответствующая нулевому зазору (натягу). Заштрихованная на рис. 3.2 площадь характеризует вероятность получения соединений с зазором, незаштрихованная – с натягом. Вся площадь под кривой соответствует общему числу сопряжений данной посадки, т. е. вероятность равна 1, или 100%. 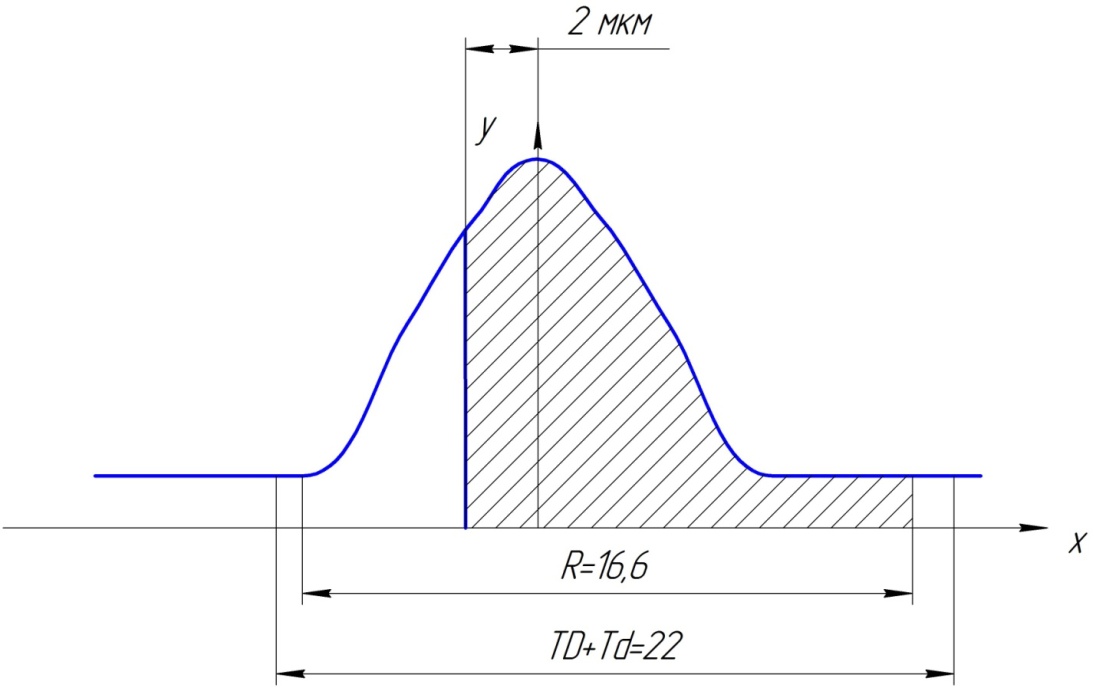 Рисунок 3.2. Кривая Гаусса для закона нормального распределения При законе нормального распределения среднее квадратическое отклонение σ определяется по формуле 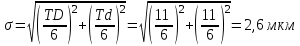 , ,где TD - допуск отверстия; Td - допуск вала, а относительное отклонениеz равно: 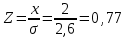 . .Определим диапазон рассеяния зазоров и натягов R , допуск посадки Т и покажем их на рис. 3.2. 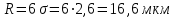 ; ;Т = TD + Td = 11+ 11 = 22 мкм. Вероятное количество сопряжений с зазором равно 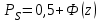 где 0,5 (50%) – половина площади под кривой Гаусса; Ф(z) – функция от z , соответствующая площади, ограниченной участком кривой между центром группирования и ординатой с нулевым зазором (натягом). Определим значение функции Ф(z) [2]: 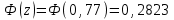 . .Таким образом, вероятное количество сопряжений с зазором (заштрихованная площадь кривой) 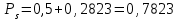 или 95,15%. Вероятное количество сопряжений с натягом 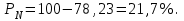 |
