Курсовая по магниторазведке. Курсовая работа по магниторазведке. Курсовая работа по магниторазведке Расчет суммарного магнитного поля для совокупности тел правильной формы
 Скачать 2.25 Mb. Скачать 2.25 Mb.
|
|
МИНОБРНАУКИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Геологический факультет Кафедра геофизики Курсовая работа по магниторазведке «Расчет суммарного магнитного поля для совокупности тел правильной формы» Выполнил: студент 2 курса, группа №7 ….. Научный руководитель: Антонов Ю.В. Воронеж 2020 СодержаниеМИНОБРНАУКИ 1 ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ 1 «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» 1 Геологический факультет 1 Кафедра геофизики 1 Курсовая работа по магниторазведке 1 «Расчет суммарного магнитного поля для совокупности тел правильной формы» 1 Введение 3 1.Краткие теоретические сведения. Общие интегральные соотношения 4 2.Магнитное поле тел правильной формы 6 2.1.Магнитное поле вертикально намагниченного горизонтального кругового цилиндра 6 2.2.Магнитное поле вертикально намагниченного вертикальный тонкого пласта 9 2.3.Расчет суммарного магнитного поля от тел правильной формы 14 Введение 3 1.Краткие теоретические сведения. Общие интегральные соотношения 4 2.Магнитное поле тел правильной формы 6 2.1.Магнитное поле вертикально намагниченного горизонтального кругового цилиндра 6 2.2.Магнитное поле вертикально намагниченного вертикальный тонкого пласта 9 2.3.Расчет суммарного магнитного поля от тел правильной формы 13 ВведениеЦелью курсовой работы является закрепление теоретических знаний, полученных в результате изучения курсов «Гравиразведка» и «Магниторазведка». Задача: рассчитать суммарное магнитное поле для трех вертикально намагниченных тел правильной формы, таких как вертикальный тонкий пласт 1, вертикальный тонкий пласт 2 и цилиндр (рис.1). 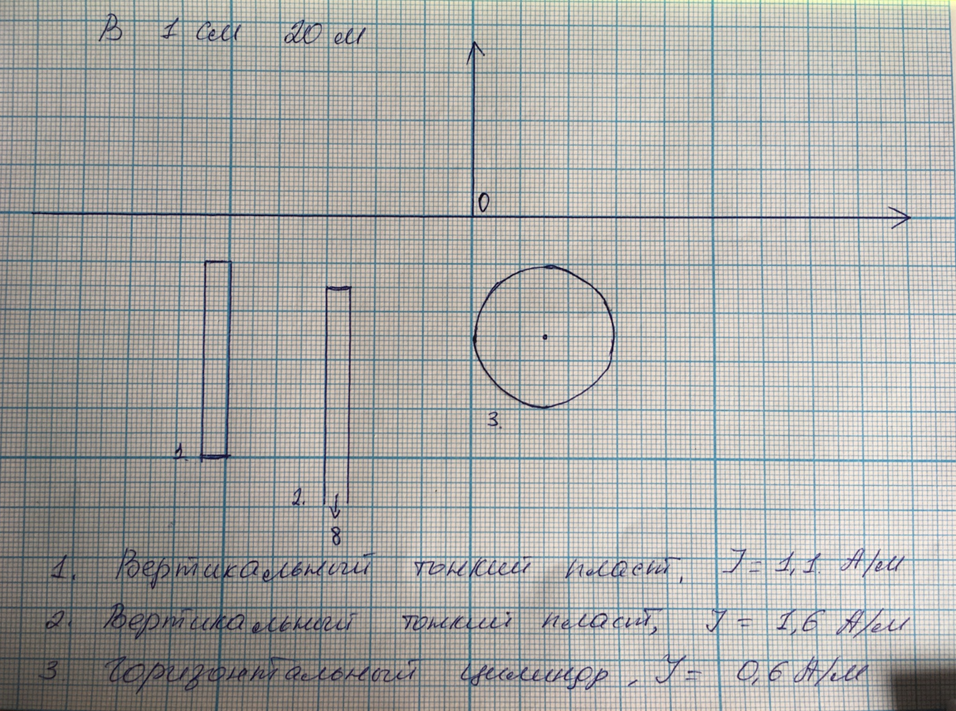 Рис. 1. Задание Параметры аномальных тел представлены в таблице №1. Таблица №1
1.Краткие теоретические сведения. Общие интегральные соотношенияПотенциал притяжения в точке с прямоугольными координатами x, y, z, лежащими вне тела определяется формулой: 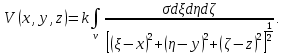 В общем случае плотность тела σ есть функция переменных интегрирования 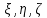 . В гравиразведке обычно рассматривают тела с постоянной плотностью. При этом условии выносят σ за знак интеграла. . В гравиразведке обычно рассматривают тела с постоянной плотностью. При этом условии выносят σ за знак интеграла.Для обозначения производных потенциала притяжения V используют индексы, указывающие координаты, по которым ведется дифференцирование. Дифференцируя равенство по x, y, z, получаем общие интегральные соотношения для трехмерных тел: 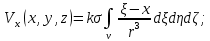 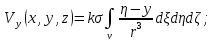 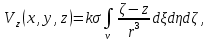 где где 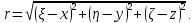 Для однородной намагниченности теоремой Пуассона устанавливается связь между гравитационным и магнитным потенциалами: 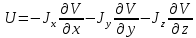 где U — магнитный потенциал тела, создающего аномалию; Jx, Jy, Jz — составляющие вектора намагниченности J; V — гравитационный потенциал тела. Составляющие вектора индукции аномального магнитного поля получаются дифференцированием выражения для магнитного потенциала по соответствующим координатам, представляющим собой проекцию вектора Тa на направление нормального магнитного поля Земли — дифференцированием по направлению Т0. Формула Пуассона лежит в основе почти всех расчетов аномального магнитного поля. Особенно простыми эти расчеты становятся для случая вертикального намагничения, когда магнитный потенциал пропорционален силе тяжести, вертикальная составляющая — вертикальному градиенту силы тяжести, горизонтальная составляющая H — горизонтальному градиенту силы тяжести, и можно заимствовать для расчетов магнитных аномалий все формулы, полученные в гравиразведке. 2.Магнитное поле тел правильной формы2.1.Магнитное поле вертикально намагниченного горизонтального кругового цилиндраЭ 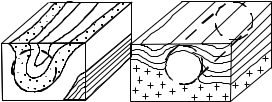 та простейшая двумерная модель играет большую роль в теории интерпретации гравитационных аномалий. Геологическими аналогами горизонтального кругового цилиндра являются: линейные антиклинальные и синклинальные складки, рвы и валы на поверхности кристаллического фундамента и коренных пород, погребенные долины и русла палеорек (рис.2). Рис.2. Геологические аналоги горизонтального кругового цилиндра Рассмотрим такое цилиндрическое тело в системе координат (x,y,z), как это показано на рис.3. 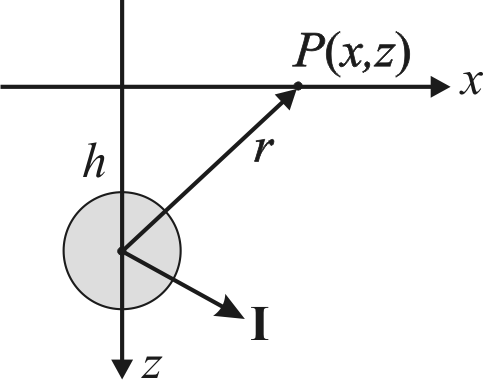 Рис.3. Модель тонкого горизонтального цилиндра Центр цилиндра находится на глубине h (м) от плоскости наблюдения z = 0. Радиус цилиндра R (м) является некоторой малой величиной (R → 0), а вектор намагничения I однороден по всему объему цилиндра. M – магнитный момент цилиндра (А*м2): 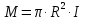 µ0 – магнитная проницаемость вакуума (Гн/м)  . .Выражения для вычисления компонент магнитной индукции от намагниченного горизонтального цилиндра приведены для случая расположения центра цилиндра под точкой начала координат (ξ=0, ζ=h). Все компоненты индукции вычисляются на профиле по x при значении z=0. Значения индукции магнитного поля переводятся в нТл (что выполняется умножением значений на величину 109). Запишем выражения: 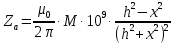 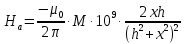 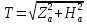 Учитывая параметры цилиндра, рассчитаем его магнитное поле (рис.4 ). 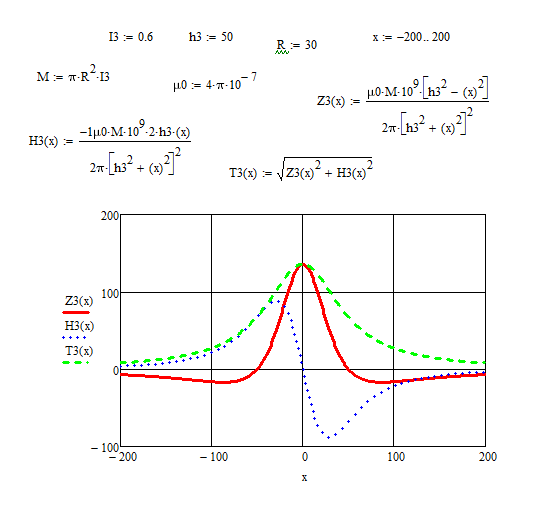 Рис.4.Магнитное поле вертикально намагниченного горизонтального цилиндра 2.2.Магнитное поле вертикально намагниченного вертикальный тонкого пластаГеологические аналоги: вертикальные пласты, дайки, зоны разломов (рис.5).  Рис.5. Геологические аналоги тонкого вертикального пласта Рассмотрим тонкий пласт в системе координат (x,y,z), как это показано на рис.6, полагая, что пласт простирается по оси y от ‑∞ до +∞. Такое тело является типичным двумерным объектом. Центр пласта расположен под точкой начала координат, а глубина до его верхней и нижней кромки равна h1 и h2. от плоскости наблюдения z = 0. Вектор намагничения J однороден по всему объему тела. 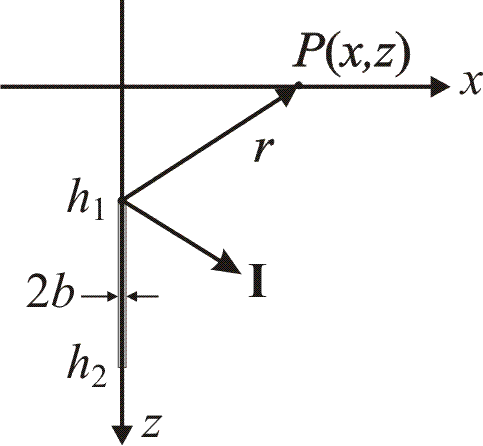 Рис.6. Модель тонкого вертикального пласта 2b – толщина пласта по оси x (2b h1µ0 – магнитная проницаемость вакуума (Гн/м). Выражения для вычисления компонент магнитной индукции от намагниченного вертикального тонкого пласта приведены для случая расположения центра пласта под точкой начала координат. Все компоненты индукции вычисляются на профиле по x при значении z=0. Значения индукции магнитного поля переводятся в нТл (что выполняется умножением значений на величину 109). Запишем выражения: 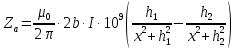 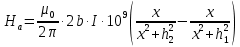 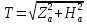 Для пласта малой мощности, безграничного на глубину и по простиранию, формулы выглядят следующим образом: 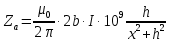 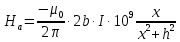 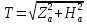 Учитывая параметры вертикального тонкого пласта1, рассчитаем его магнитное поле (рис.7 ). 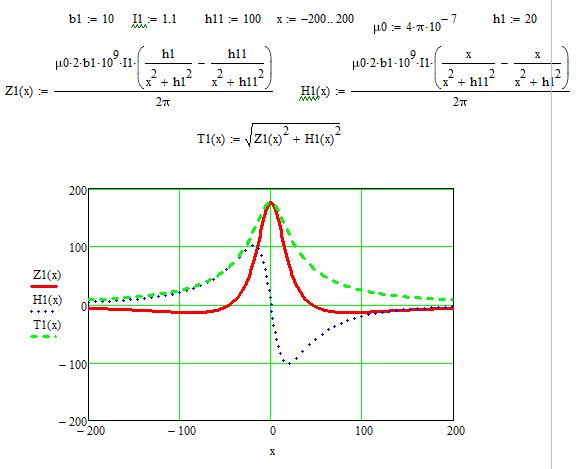 Рис.7.Магнитное поле Вертикального тонкого пласта 1 Учитывая параметры вертикального тонкого пласта2, рассчитаем его магнитное поле (рис.8 ). 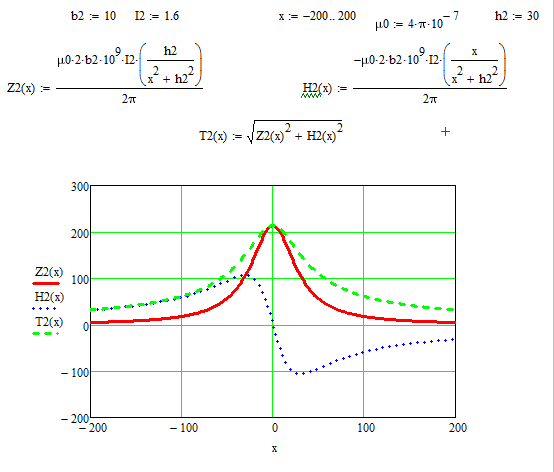 Рис.8.Магнитное поле вертикального тонкого пласта 2 2.3.Расчет суммарного магнитного поля от тел правильной формыЧтобы рассчитать магнитное поле от трех тел нужно учесть смещения этих объектов относительно начала координат. Это можно сделать двумя способами. В первом случае смещение можно внести в формулу по координате х, например: 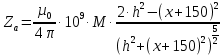 Во втором – это смещение можно учесть непосредственно при построении графика. После этого магнитные поля от трех тел необходимо суммировать. В результате получим график, магнитного поля обусловленного тремя объектами (рис.9). 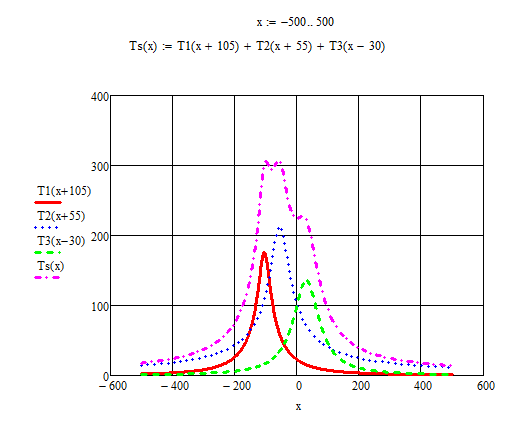 Рис.9.Суммарное магнитное поле |
