ИЗМЕРЕНИЕ ЛИНЕЙНЫХ РАЗМЕРОВ И ОБЪЕМОВ ТВЕРДЫХ ТЕЛ ПРАВИЛЬНОЙ ФОРМЫ. лаба 1. Лабораторная работа 1 измерение линейных размеров и объемов твердых тел правильной формы студентка гр. Фм1218
 Скачать 20.35 Kb. Скачать 20.35 Kb.
|
|
Федеральное государственное образовательное учреждение высшего образования «Чувашский государственный университет им. И. Н. Ульянова» Кафедра общей физики Лабораторная работа №1 ИЗМЕРЕНИЕ ЛИНЕЙНЫХ РАЗМЕРОВ И ОБЪЕМОВ ТВЕРДЫХ ТЕЛ ПРАВИЛЬНОЙ ФОРМЫ Выполнила: студентка гр. ФМ-12-18 Шерстобитова Дарья Николаевна Принял: доц. Петров Н. И. г. Чебоксары 2021 Приборы и принадлежности: штангенциркуль, микрометр, масштабная линейка, набор тел правильной формы. Цель работы – ознакомление с основными положениями теории погрешностей, статистической обработкой результатов измерений, а также правилами и приемами измерений линейных и угловых величин. Краткая теория: Объем цилиндрического кольца можно определить по его линейным размерам на основании формулы 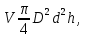 где D, d – внешний и внутренний диаметры кольца; h – толщина кольца. Что такое доверительный интервал и доверительная вероятность? Мы можем найти, с какой вероятностью Р хист окажется в любом интервале значений (x –х, x + х). Эта вероятность определяется выражением 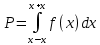 и называется доверительной вероятностью, или надежностью. Она равна площади заштрихованной фигуры. Интервал (x –х, x + х) называется доверительным. Как находится абсолютная погрешность прямых измерений? Как вычислить абсолютные и относительные погрешности косвенных измерений? Как оцениваются приборные погрешности? Если точность прибора не указана, то абсолютную погрешность прибора обычно принимают равной половине цены наименьшего деления шкалы прибора. Согласно ГОСТу, электроизмерительные приборы делятся на восемь классов точности: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. По классу точности прибора можно определить абсолютную и относительную погрешности: 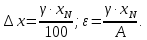 Чему равна погрешность табличных значений? При использовании табличных величин их следует округлять так, чтобы их точность превышала точность измеряемых величин на одну значащую цифру, тогда погрешностью табличных величин можно пренебречь. Если табличные значения, данные установки записаны без указания погрешности или определены не очень точно, то обычно считается, что их погрешность равна половине единицы последнего указанного разряда. Как устроен линейный нониус, где он применяется и чему равна его точность? Нониусом называется дополнительная шкала к обычному масштабу, позволяющая повысить точность измерений в 10-20 раз. Линейный нониус представляет собой небольшую шкалу, скользящую вдоль основной шкалы. Деления на нониусе наносятся так, чтобы длина m делений нониуса была равна длине m-1 делений основной шкалы. Если число делений нониусной шкалы m, а цена деления основной шкалы y, тогда x m m 1y , где x – цена деления нониуса. Величина, определяемая разностью y x y/m называется точностью нониуса. Точность нониуса равна отношению цены деления основной шкалы к числу делений нониуса. Она определяет максимальную погрешность нониуса. Измерения
Обработка результатов измерений 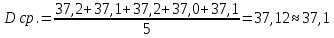 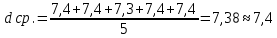 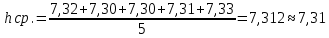 Δ D = Dср – D; Δ d = dср – d; Δ h = hср – h. Вычислим среднеквадратичные погрешности отдельных измерений, мм 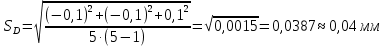 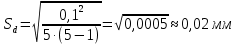 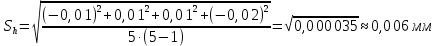 Принимаем значение надёжности Р = 0,95 и коэффициент Стьюдента для пяти измерений αp,n = 2,8. Вычислим случайные погрешности, мм Dсл = 2,8 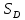 = 0,112 = 0,112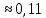 ; ; dсл = 2,8 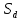 = 0,056 = 0,056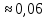 ; ; hсл = 2,8 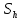 = 0,0168 = 0,0168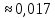 . .Полная погрешность с учетом приборной, мм Δ D = 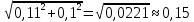 ; ;Δ d = 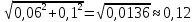 ; ;Δ h = 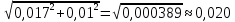 . .Запишем результаты прямых измерений, мм D = (37,10 0,15); d = (7,40 0,12); h = (7,310 0,020). Среднее значение объема кольца, мм3 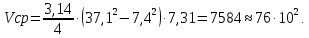 Относительную погрешность объема вычислим по формуле 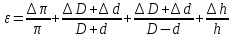 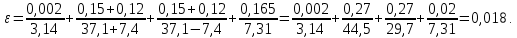 Абсолютную погрешность измерения объема кольца, мм3 V = ε Vср; V = 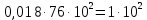 . .Записываем окончательный результат измерения объема, мм 3 V = (76 1) 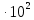 , Р = 0,95. , Р = 0,95.Вывод: Истинное значение объёма данного кольца с вероятностью 95% лежит в найденном интервале. Я ознакомилась с основными положениями теории погрешностей, статистической обработкой результатов измерений, а также правилами и приемами измерений линейных и угловых величин, методом Стьюдента. |
