Курсовая работа передаточная функция. Курсовая работа по мдк 01. 03. Теоретические основы контроля и анализа функционирования систем автоматического управления
 Скачать 2.5 Mb. Скачать 2.5 Mb.
|
|
Z1 – апериодическое звено первого порядка: К=0,7;Т1=9. Z2 – апериодическое звено второго порядка: K=0,6 T1=20 T2=4 Z3 – усилительное звено:К=7. Z4 – интегрирующие звено : K=0,65. Z5 – апериодическое звено первого порядка: К=6 ;Т1=9с. Передаточные функции функциональных звеньев примут вид: Z1 – апериодическое звено первого порядка: 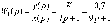 Z2 – апериодическое звено второго порядка: 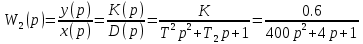 Z3 – усилительное звено: 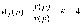 Z4 – интегрирующее звено: 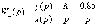 Z5 – апериодическое звено первого порядка: 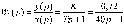 3. Расчет передаточной функции Система автоматического управления автоматического управления реверсивным переключателем для асинхронного двигателя С учетом составленных передаточных функций структурная схема системы автоматического управления адаптивной системы с эталонной моделью примет вид рис.42     -s1 ы   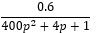           +s2      7   Определим передаточную функцию модуля САУреверсивным переключателем для асинхронного двигателя Для этого преобразуем структурную схему (рис. 42) в эквивалентную с передаточной функцией всей системы автоматического управления. Передаточные функции отдельных элементов и входной сигнал известны. Определим передаточную функцию САУ. Для записи передаточной функции сложной структурной схемы ее необходимо преобразовать в соответствии с правилами преобразования структурных схем. Произведем последовательное преобразование отдельных участков. 1)звено 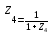 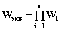 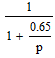 Рис. 43.Первое преобразование. 2) Звенья Z2, Z4 соединены последовательно-согласно. 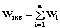 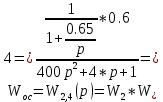 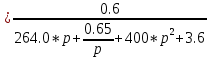 Рис. 44.Второе преобразование. 3) Звенья Z2,Z4,Z3 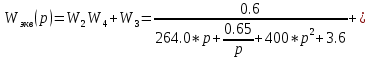 7= 7=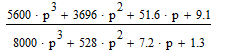 = В результате проведенных преобразований получаем эквивалентное звено с передаточной функцией всей системы САУ. Главная передаточная функция замкнутой цепи: 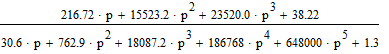 4) 4) 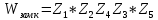 = =Характеристическое уравнение САУ реверсивным переключателем для асинхронного двигателя 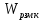 = =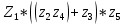 = =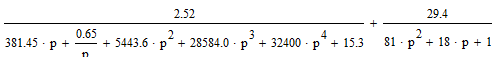 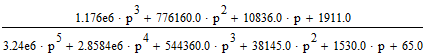 = 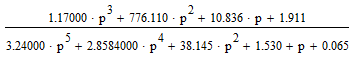 = Характеристическое уравнение САУ реверсивным переключателем для асинхронного двигателя 4. Расчет и построение частотных характеристик разомкнутой САУ Зная передаточную функцию звена W(p) легко получить все его частотные характеристики. Для этого необходимо подставить в нее j вместо p, получим АФЧХ W(jω). Затем надо выразить из нее ВЧХ P( ) и МЧХ (Q(ω). После этого преобразуют АФЧХ в показательную форму и получают АЧХ A( ) и ФЧХ ϕ(ω), а затем определяют выражение ЛАЧХ L(w) = 20lgA(ω) (ЛФЧХ отличается от ФЧХ только масштабом оси абсцисс). W(j  ), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называется частотной передаточной функцией. Легко заметить, что она может быть получена путем простой замены p на j ), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называется частотной передаточной функцией. Легко заметить, что она может быть получена путем простой замены p на j в выражении W(p). в выражении W(p).W(j  ) есть комплексная функция, поэтому: ) есть комплексная функция, поэтому: где P(  ) - вещественная ЧХ (ВЧХ); Q( ) - вещественная ЧХ (ВЧХ); Q( ) - мнимая ЧХ (МЧХ); А( ) - мнимая ЧХ (МЧХ); А( ) - амплитудная ЧХ (АЧХ): ) - амплитудная ЧХ (АЧХ): 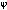 ( ( ) - фазовая ЧХ (ФЧХ). АЧХ дает отношение амплитуд выходного и входного сигналов, ФЧХ - сдвиг по фазе выходной величины относительно входной: ) - фазовая ЧХ (ФЧХ). АЧХ дает отношение амплитуд выходного и входного сигналов, ФЧХ - сдвиг по фазе выходной величины относительно входной: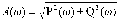 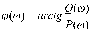 Если W(jω) изобразить вектором на комплексной плоскости, то при изменении ω от 0 до +  его конец будет вычерчивать кривую, называемую годографом вектора W(jω), или амплитудно - фазовую частотную характеристику (АФЧХ). Ветвь АФЧХ при изменении ω от - его конец будет вычерчивать кривую, называемую годографом вектора W(jω), или амплитудно - фазовую частотную характеристику (АФЧХ). Ветвь АФЧХ при изменении ω от -  до 0 можно получить зеркальным отображением данной кривой относительно вещественной оси. до 0 можно получить зеркальным отображением данной кривой относительно вещественной оси.В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ): логарифмическая амплитудная ЧХ (ЛАЧХ) L(  ) и логарифмическая фазовая ЧХ (ЛФЧХ) ) и логарифмическая фазовая ЧХ (ЛФЧХ) 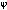 ( ( ). Они получаются путем логарифмирования передаточной функции: ). Они получаются путем логарифмирования передаточной функции: 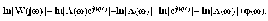 ЛАЧХ получают из первого слагаемого, которое из соображений масштабирования умножается на 20, и используют не натуральный логарифм, а десятичный, то есть L(  ) = 20lgA( ) = 20lgA( ). Величина L( ). Величина L( ) откладывается по оси ординат в децибелах. Изменение уровня сигнала на 10 дб соответствует изменению его мощности в 10 раз. Так как мощность гармонического сигнала Р пропорциональна квадрату его амплитуды А, то изменению сигнала в 10 раз соответствует изменение его уровня на 20дб,так как ) откладывается по оси ординат в децибелах. Изменение уровня сигнала на 10 дб соответствует изменению его мощности в 10 раз. Так как мощность гармонического сигнала Р пропорциональна квадрату его амплитуды А, то изменению сигнала в 10 раз соответствует изменение его уровня на 20дб,так какlg(P2/P1) = lg(A22/A12) = 20lg(A2/A1). По оси абсцисс откладывается частота w в логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соответствует изменение w в 10 раз. Такой интервал называется декадой. Так как lg(0) = -  , то ось ординат проводят произвольно. , то ось ординат проводят произвольно.ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси . Величина ( ) откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: -   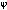  + +  ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно восстановить ее передаточную функцию и определить параметры. При исследовании и проектировании САУ часто используют АФЧХ, ЛАЧХ и ЛФЧХ разомкнутых систем. Это объясняется тем, что разомкнутые САУ более просто исследовать экспериментально, чем замкнутые. В то же время по ним можно получить исчерпывающую информацию о поведении данной САУ в замкнутом состоянии. Любую многоконтурную САУ можно привести к одноконтурной. Разомкнутая одноконтурная САУ состоит из цепочки последовательно соединенных динамических звеньев. Зная передаточную функцию разомкнутой САУ можно построить ее ЧХ. И наоборот, зная ЧХ разомкнутой САУ, снятую, например, опытным путем, можно найти ее передаточную функцию. . Передаточная функция разомкнутой САУ 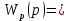 Приравняем знаменатель передаточной функции разомкнутой САУ к нулю, получим характеристическое уравнениеразомкнутой САУ. Для исследования заменим оператор дифференцирования pна jω в выражении получим ее АФЧХ: Амплитудная фазовая частотная характеристика АФЧХ 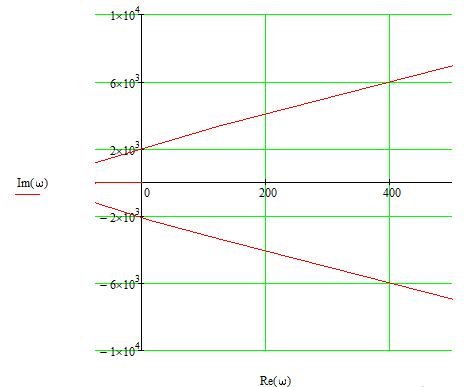 Рис. 46.Амплитудная фазовая частотная характеристика. Вещественная частотная характеристика ВЧХ: 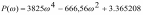 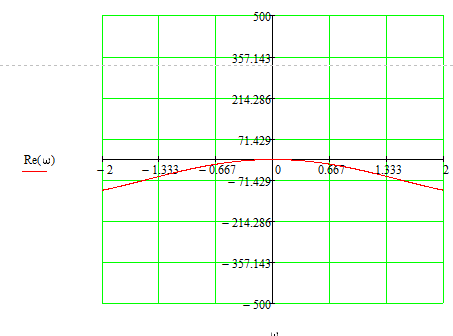 Рис. 47.Вещественная частотная характеристика. Мнимая частотная характеристика МЧХ: 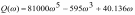 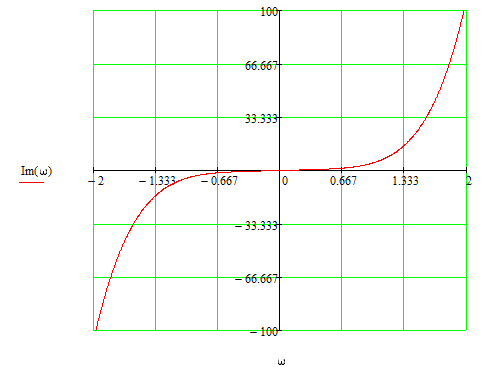 Рис. 48.Мнимая частотная характеристика. Амплитудно-частотная характеристика АЧХ 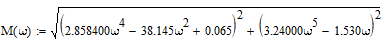 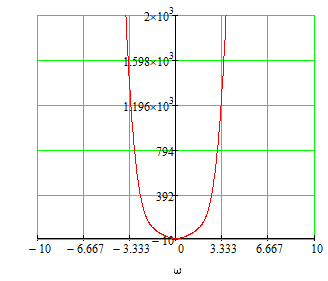 Рис. 49.Амплитудно-частотная характеристика. Фазовая частотная характеристика ФЧХ 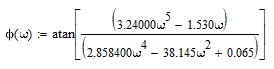 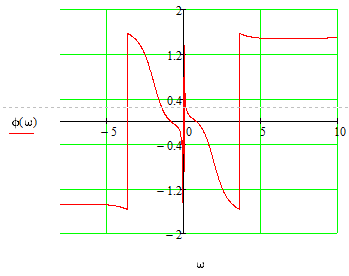 Рис. 49.Фазовая частотная характеристика. 5. Построение переходного процесса на ЭВМ Временными характеристиками системы называются зависимости выходной величины от времени при входной величине, изменяющейся по заданному закону. В качестве таких характеристик рассматривается переходная и весовая функции. Переходную функцию можно получить как решение неоднородного дифференциального уравнения системы, правой частью которого является единичная ступенчатая функция. Выражение для переходной функции будет иметь вид 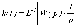 , , Реакция САУ на единичную импульсную функцию при условии, что система до приложения воздействия находилась в покое, называется весовой функцией w(t). 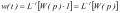 , , тогда 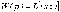 , , то есть передаточную функцию системы автоматического управления можно определить как изображение по Лапласу весовой функции. Расчет и построение временных характеристик осуществляем с применением програмной среды MathCAD. MathCAD является математическим редактором, позволяющим проводить разнообразные научные и инженерные расчеты, начиная от элементарной арифметики и заканчивая сложными реализациями численных методов. Переходный процесс для замкнутой системы САУ с передаточной функцией 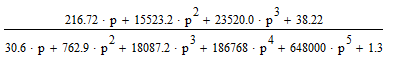 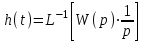 = = 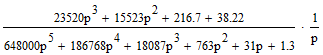 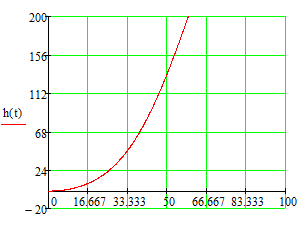 Рис. 50.Переходная характеристика. Импульсная переходная характеристика САУ 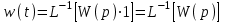 = =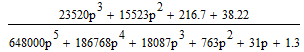 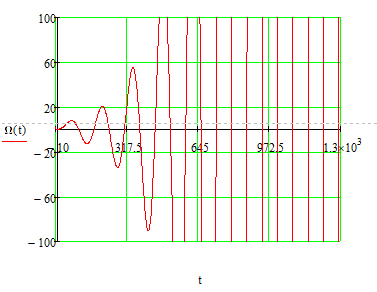 Рис. 51.Импульсная переходная. 6. Определение устойчивости САУ Свойства устойчивости проявляются в способности системы возвращаться в первоначальное состоянии или близкое к нему при приложении к системе или снятии воздействия. В связи с этим различают три ситуации: 1) система устойчива; 2) система неустойчива; 3) система "безразличная", нейтральная. Оценить устойчивость системы можно в результате исследования ее математической модели, то есть решить соответствующую систему дифференциальных уравнений. Различают алгебраические и частотные критерии устойчивости. Алгебраические: критерий Раусса; критерий Гурвица; критерий Вышнеградского; Частотные: критерий Михайлова; критерий Найквиста; Для проверки устойчивости в курсовой работе будем использовать алгебраический критерий устойчивости Гурвица и частотный критерий Михайлова. Оценка устойчивости по критерию устойчивости Гурвица На основании характеристического уравнения системы 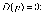 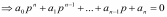 . .строится определитель Гурвица (при 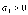 ). ).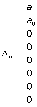 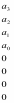 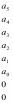 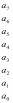 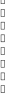  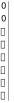  Свободные места заполняются нулями. Свободные места заполняются нулями.Для устойчивости системы необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительны. Диагональные миноры: 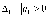 ; ; 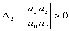 ; ; 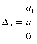 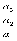 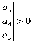 ; . . . ; . . .Задачу будем решать с использованием формулировки критерия устойчивости по Гурвицу. Для этого необходимо из коэффициентов характеристического уравнения составить главный определитель Гурвица по определенному правилу: вдоль главной диагонали записываются коэффициенты, начиная c an-1, выше главной диагонали записываются коэффициенты с индексом на единицу меньше, ниже главной диагонали записываются коэффициенты с индексом на единицу больше. Порядок определителя соответствует порядку характеристического уравнения. Из этого определителя составляются диагональные миноры, которых должно быть n-1. Система автоматического управления будет устойчивой тогда и только тогда, когда все диагональные миноры главного определителя будут положительны. Для определения устойчивости изпользуем передаточную функцию для замкнутой системы САУ. 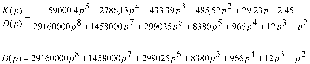 Для нашей задачи главный определитель Гурвица имеет вид 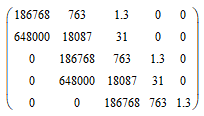 Рассчитаем диагональные миноры 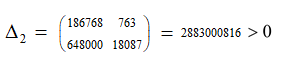 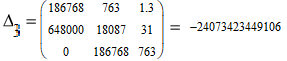 Все диагональные миноры кроме 3 положительны, следовательно, система неустойчива. Следует отметить, что для исследования устойчивости не обязательно вычислять все миноры. Если при вычислении миноров получают, что его значение отрицательно, дальнейшие расчеты можно прекратить и сделать вывод, что система неустойчива. |
