Курсовая работа передаточная функция. Курсовая работа по мдк 01. 03. Теоретические основы контроля и анализа функционирования систем автоматического управления

Название	Курсовая работа по мдк 01. 03. Теоретические основы контроля и анализа функционирования систем автоматического управления
Анкор	Курсовая работа передаточная функция
Дата	22.06.2022
Размер	2.5 Mb.
Формат файла
Имя файла	KURSOVAYa_peredatochnaya_funktsia_gotovaya (2).docx
Тип	Курсовая #609889
страница	4 из 4

1 2 3 4

Оценка устойчивости по критерию устойчивости Михайлова
Исследуем эту же систему автоматического управления на устойчивость с использованием частотного критерия устойчивости Михайлова.

В соответствии с этим критерием необходимо построить годограф Михайлова, который для устойчивых систем имеет строго определенный вид. И тогда система автоматического управления будет устойчивой, если годограф Михайлова начинается на положительной вещественной полуоси, обходит последовательно, нигде не обращаясь в нуль, n квадрантов координатной плоскости, уходя в бесконечность в п квадранте, где n - порядок характеристического уравнения.

Для записи математического выражения годографа Михайлова необходимо в характеристическом уравнении перейти в частотную область, т.е. в уравнении сделать замену - s = iω. В результате получим комплексное выражение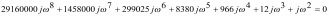

Рассмотрим степени мнимой единицы:

i;

i²=-1;

i³= i² i=- i;

i⁴= i³i=- i i=- i2=-(-1)=1;

i⁵= i⁴ i= i;

i⁶= i⁵ i= i i= i2=-1;

i⁷= i⁶ i=-1 i=- i;

i⁸= i⁷ i=- i i=- i2=1.
Выделим вещественную часть –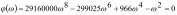

и мнимую часть –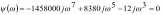

Первая называется вещественной функцией Михайлова, а вторая - мнимой функций Михайлова.

По вещественной и мнимой функциям Михайлова строится годограф Михайлова в координатах φ(ω)-ψ(ω) методом контрольных точек. Для этого задается значение частоты, для которой определяются значения функций φ(ω)-ψ(ω).График годографа Михайлова представлен на рис. 52, его анализ показывает, что годограф начинается на вещественной положительной полуоси и располагается только в первом квадранте, что свидетельствует о том, что система неустойчива.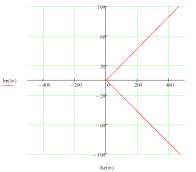

Рис. 52.Годограф Михайлова.

7. Определение основных показателей качества
Основными показателями качества регулирования являются быстродействие, колебательность и перерегулирование, характеризующие точность и плавность протекания процесса. Эти показатели оценивают по переходной характеристике системы, являющейся графиком переходной функции h(t).

Переходная функция описывает изменение выходной величины системы, когда на ее выход подается единичное ступенчатое воздействие при нулевых начальных условиях.

Основные оценки качества регулирования:

а) tp – время регулирования. Минимальное время, по истечении которого регулируемая величина не будет отклоняться от установленного значения больше, чем на заданную точность δ;

б) перерегулирование σ. Максимальное отклонение переходной характеристики от установившегося значения, выраженное в долях или процентах
Динамика САУадаптивной системы с эталонной моделью.
Частотный анализ показал, что при увеличении частоты происходит возрастание амплитуды колебательного процесса при сдвиге фазы и установлении ее после частоты ω=0,4 при более высоких частотах сдвига фазы практически не происходит.

Расчеты показали что система подчиняется закону интегрирующего звеньев. Интегрирующие звенья представляет собой интегратор W(p) = 1/p. Интегрирующее звено неограниченно "накапливает" входное воздействие, что показала переходная характеристика. Примеры интегрирующих звеньев: электродвигатель, поршневой гидравлический двигатель, емкость и т.п. Введение его в САУ превращает систему в астатическую, то есть ликвидирует статическую ошибку.

При подаче на вход импульсного сигала также отмечается накопление входного воздействия при этом возникает затухающий колебательный процесс, за что отвечает колебательное звено порядка. Так как решение уравнения зависит от соотношения постоянных времени T₁ и T₂, которое определяет коэффициент затухания

r =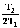

.

Можно записать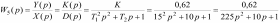

r=T₂/2T₁=15/2*10=0.75

При r<1 корни полинома знаменателя W(p) комплексно сопряженные: p_1,2 =

± j

. Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс с затуханием

и частотой

. Такое звено называется колебательным.

Следовательно можно сделать вывод, что за счет действия отрицательной обратной связи в контуре эта ошибка будет сведена к нулю, поскольку любой устойчивый контур с отрицательной обратной связью сводит ошибку к нулю

Список используемой литературы

Келим Ю.М. Контроль и метрологическое обеспечение средств и систем автоматизации: учебник для студ. Учрежд. СПО. - М.: Издательский центр «Академия», 2014. - 352с.
Дополнительные источники:
Шишмарев В.Ю. Автоматика. - М.: Издательский центр «Академия», 2010.
Колчков В. И. Метрология, стандартизация и сертификация. - М.: Владос, 2010.
Зайцев С. А. Метрология, стандартизация и сертификация в энергетике. - М.: Издательский центр «Академия», 2009
Келим Ю.М. «Типовые элементы систем автоматического управления», учебное пособие. - М.:ИНФРА-М, 2004.
Лазарева Т.Я. Основы теории автоматического управления. - Т.: Издательство ТГТУ, 2004.
Камразе А.Н., Фитерман М.Я. «Контрольно-измерительные приборы и автоматика», учебник.- Л. Химия, 1988
Адаптивные системы автоматического управления: учебное пособие / В. Н. Антонов, А.М. Пришвин, В. А. Терехов, А. Э. Янчевский; подред. В. Б. Яковлева. Ленинград: Изд-во Ленингр. ун-та, 1984.
Александровский Н. М., Егоров С. В., Кузин Р. Е. Адаптивные системы автоматического управления сложными технологическими объектами / Под общ. ред.Н. М. Александровского. М.: Энергия, 1973.
Атанс М., Фальб П. Оптимальное управление. М.: Машиностроение, 1968.
Бугров С. В., Жмудь В. А., Колкер А.Б. Применение метода разделения движения для стабилизации лазерного излучения // Сб. научн. тр. НГТУ. Новосибирск. 2010. №2 (60). С. 3–8.
Бугров С. В., Лисовой Р. А., Жмудь В. А., Колкер А. Б. Адаптивная система управления с использованием стабилизирующего эффекта девиации коэффициента регулятора // Научный вестник НГТУ. 2010. № 1(38). С. 157–160.
Власов К. П. Теория автоматического управления: учебное пособие. Харьков: Гуманитарный центр, 2007.
Воронов А. В. Основы теории автоматического управления. М.; Л.: Энергия, 1965. Т. 1, 2.
Жмудь В. А. Моделирование и оптимизация систем управления лазерным излучением в среде VisSim: учебное пособие. Новосибирск: НГУ, 2009.
Жмудь В. А. Прецизионные системы управления лазерным излучением: учеб. Пособие Новосибирск: НГУ, 2005.
[10] Ишимцев Р. Ю. Обоснование структуры и критериев оптимизации САУ непрерывного технологического процесса // Сборник научных трудов НГТУ. Новосибирск, 2008. № 2(52). С. 3–10.
Ким Д. П. Теория автоматического управления. Многомерные, нелинейные, оптимальные и адаптивные системы. 2-е изд., испр. и доп. М.: ФИЗМАТЛИТ. 2007. Т. 2.
Кунцевич В. М., Лычак М. М. Синтез оптимальных и адаптивных систем управления. Игровой подход. Киев: Наукова думка, 1985.
Куропаткин П. В. Теория автоматического управления: учебное пособие для электротехн. специальностей вузов. М.: Высш. шк., 1973.
Методы классической и современной теории автоматического управления: учебник в 5 т. / Под ред. К. А. Пупкова, Н. Д. Егупова. М.: Изд-во МГТУ им. Н. Э. Баумана. 2004. т. 5. Методы современной теории автоматического управления.
Самонастраивающиеся системы. Справочник / Под ред. П. И. Чинаева. Киев: Наукова думка, 1969.
Солодовников В. В. Статистическая динамика линейных систем автоматического управления. М.: Физматгиз, 1960.
Теория автоматического управления: учеб. Для вузов по спец. «Автоматика и телемеханика»: в 2 ч. 2-е изд. / А. А. Воронов, Д. П. Ким, В. М. Лохин и др.; под ред. А. А. Воронова. М.: Высш. шк., 1986. Ч. II. Теория нелинейных и специальных систем автоматического управления.
Чаки Ф. Современная теория управления. Нелинейные, оптимальные и адаптивные системы / Пер. с англ.; под ред. Н. С. Райбмана. М.: Мир, 1975.
Detecting Process Variations in Low-End PID Autotuners. Alberto Leva, GianAntonio Magnani. 2002 IFAC. 15th Triennial World Congress, Barcelona, Spain.

1 2 3 4