Курсовая_работа_ИМТП Daler. Курсовая работа по предмету Идентификация и моделирование технологических процессов
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
|
МИНИСТЕРСТВО ВЫСШЕГО и СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН ТАШКЕНТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. И.А.КАРИМОВА Факультет «Электроника и Автоматика» Кафедра «Автоматизация производственных процессов» КУРСОВАЯ РАБОТА По предмету «Идентификация и моделирование технологических процессов» Задача: Моделирование системы управления конденсатором на основе анализа уравнений динамики процесса. Выполнила студент: Рузикулов Д гр.141-19 Направление: АиУТПП Шифр: 5311000 Руководитель проекта: д.т.н. профессор Мухитдинов Д.П. Ташкент 2022г. Оглавление: Введение Постановка задачи Краткое описание теплообменного процесса Математическое описание процесса Результаты моделирования Приложение Заключение Список используемой литературы Введение Современное нефтехимическое производство – это комплекс химико-технологических стадий, информационных систем управления и коммуникаций, планово-экономических и маркетинговых служб, научно-технологических и проектных центров. Все более возрастающее значение в процессе функционирования нефтехимического комплекса приобретают информационные системы управления и передачи данных, что объясняется интенсивным развитием цифровой техники и способов обработки информации. В этой связи весьма целесообразно применение методов математического моделировании в решении задач анализа и синтеза химико-технологических процессов, а также в задачах построения систем управления данными процессами. Математическое моделирование является эффективным инструментом определения оптимальных управляющих параметров, особенно в случае процессов, физические и химические закономерности которых достаточно изучены. При этом определение управляющих параметров может осуществляться путем расчета математической модели объекта в широком диапазоне внешних возмущений. Владение навыками составления математического описания, а также знание моделей ХТП могут быть весьма эффективными и полезными прежде всего для операторов, инженеров и специалистов в области управления и автоматизации технологических процессов. Данная курсовая работа посвящена разработке программного обеспечения для моделирования теплообменного процесса, а также нахождению значений по данным, полученным в результате данных, полученных с датчиков в теплообменнике. При эксплуатации оборудования также возможны изменения состава газовой смеси, расхода смеси, изменения температурного режима и т.д. Моделирование таких процессов является важным этапом при изменении характеристик на реальном объекте, поскольку требуется анализ возможных реакций на воздействия. Постановка задачи Моделирование системы управления конденсатором на основе анализа уравнений динамики процесса. Задание: – исследовать процесс функционирования кожухотрубного конденсатора, предназначенного для конденсации пара в органической жидкости и паров воды; – составить динамическую модель процесса; – определить расход охлаждающего агента (воды) в дискретные моменты времени, обеспечивающий полную конденсацию паров; – зависимость значения расхода охлаждающего агента, расхода паров, а также температуры охлаждающего агента на выходе аппарата от времени представить в табличном и графическом виде; – разработать презентацию курсовой работы и подготовить доклад к защите. Исходные данные и допущения: 1) длительность процесса определяется временем выхода на установившийся режим; 2) расход паров органической жидкости и паров воды на входе теплообменника (подаются в межтрубное пространство) задан в виде функции времени Gп(τ); 3) удельная теплота конденсации смеси r; 4) температура конденсации в дефлегматоре tk; начальная температура охлаждающего агента tx.н.; 5) теплофизические свойства охлаждающего агента: плотность ρx, теплопроводность λx, динамическая вязкость µx, удельная теплоемкость cx; 6) теплофизические свойства конденсата при температуре конденсации: плотность ρk, теплопроводность λk, динамическая вязкость µk; 7) параметры теплообменника (вертикального): диаметр кожуха D, диаметр трубок dт, число ходов z, число труб n, длина труб L, поверхность теплообмена F. Вариант задания 1Ж.
Краткое описание теплообменного процесса. Перенос энергии в форме тепла, происходящий между телами, имеющими различную температуру, называется теплообменом. Движущей силой любого процесса теплообмена является разность температур более нагретого и менее нагретого тел, при наличии которой тепло самопроизвольно, в соответствии со вторым законом термодинамики, переходит от более нагретого к менее нагретому телу. Различают три принципиально различных элементарных способа распространения тепла: теплопроводность, конвекцию и тепловое излучение. Теплопроводность представляет собой перенос тепла вследствие беспорядочного (теплового) движения микрочастиц, непосредственно соприкасающихся друг с другом. Конвекцией называется перенос тепла вследствие движения и перемешивания макроскопических объемов газа или жидкости. Тепловое излучение – это процесс распространения электромагнитных колебаний с различной длиной волн, обусловленный тепловым движением атомов или молекул излучающего тела. В реальных условиях тепло передается не каким-либо одним из указанных выше способов, а комбинированным путем. Например, при теплообмене между твердой стенкой и газовой средой тепло передается одновременно конвекцией, теплопроводностью и излучением. Перенос тепла от стенки к газообразной (жидкой) среде или в обратном направлении называется теплоотдачей. Еще более сложным является процесс передачи тепла от более нагретой к менее нагретой жидкости (газу) через разделяющую их поверхность или твердую стенку. Этот процесс носит название теплопередачи. В непрерывно действующих аппаратах температуры в различных точках не изменяются во времени и протекающие процессы теплообмена являются установившимися (стационарными). В периодически действующих аппаратах, где температуры меняются во времени (при нагревании или охлаждении), осуществляются неустановившиеся, или нестационарные, процессы теплообмена. В химической промышленности широко распространены тепловые процессы – нагревание и охлаждение жидкостей, конденсация паров, испарение жидкостей, которые проводятся в теплообменных аппаратах, называемых теплообменниками. Теплообменники предназначены для передачи тепла от одних веществ к другим. Вещества, участвующие в процессе передачи тепла, называются теплоносителями. Теплоносители, имеющие более высокую температуру, принято называть нагревающими агентами, а теплоносители с более низкой температурой, чем среда, от которой они воспринимают тепло, – охлаждающими агентами. В зависимости от способа передачи тепла различают две основные группы теплообменников: 1) поверхностные теплообменники, в которых перенос тепла между обменивающимися теплом веществами происходит через разделяющую их поверхность теплообмена – глухую стенку; 2) теплообменники смешения, в которых тепло передается от одной среды к другой при их непосредственном соприкосновении. Поверхностные теплообменники широко распространены и их конструкции весьма разнообразны. На рис. 1.1 показан кожухотрубчатый теплообменник жесткой конструкции, который состоит из корпуса, или кожуха 1, и приваренных к нему трубных решеток 2. В трубных решетках закреплен пучок труб 3. К трубным решеткам крепятся крышки 4. В теплообменнике одна из сред I движется в межтрубном пространстве, а другая II – внутри труб (в трубном пространстве). Среды обычно направляют противотоком друг к другу. При этом нагреваемую среду направляют снизу вверх, а среду, отдающую тепло, – в противоположном направлении. Такое направление движения каждой среды совпадает с направлением, в котором стремится двигаться данная среда под влиянием изменения ее плотности при нагревании или охлаждении.  Рис. 1.1. Кожухотрубный одноходовой (а) и многоходовой (б)теплообменники Расчет теплообменника с известной поверхностью теплопередачи заключается, как правило, в определении конечных температур теплоносителей при их известных начальных значениях, а также в определении требуемых расходов нагревающего или охлаждающего агентов. Математическое описание теплообменного процесса Расчет тепловой нагрузки Согласно основному уравнению теплопередачи, тепловой поток Q (расход передаваемой теплоты, тепловая нагрузка) определяется следующим образом: Q=FK∆tср, (1.1) где F – поверхность теплопередачи (м2), К – коэффициент теплопередачи (Вт/(м2·К)), ∆tср– средний температурный напор (средняя движущая сила) (К). Тепловую нагрузку Q при известных значениях расхода и теплофизических свойств теплоносителей можно рассчитать следующим образом: если агрегатное состояние одного из теплоносителей не меняется, то Q=Gc(tн – tк) или Q = Gc(tк −tн), (1.2) где G – расход теплоносителя (кг/с), с – удельная теплоемкость теплоносителя (Дж/(кг·град)) при средней температуре 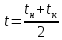 tн, tк – начальная и конечная температуры (К); 2) при конденсации насыщенных паров без охлаждения конденсата или при кипении Q=Gr (1.3) здесь r – теплота конденсации (Дж/кг); при конденсации перегретых паров с охлаждением конденсата Q=G (Iн– ctк), (1.4) где Iн – энтальпия (теплосодержание) пара (Дж/кг). Один какой-либо технологический параметр, не указанный в исходном задании (расход одного из теплоносителей или одна из температур), можно найти с помощью уравнения теплового баланса, приравнивая правые части уравнений (1.2) – (1.4) для горячего и холодного теплоносителей. В аппаратах с прямо- и противоточным движением теплоносителей средняя разность температур потоков ∆tср определяется как средне логарифмическая между большей ∆tб и меньшей ∆tм разностями температур теплоносителей на концах аппарата: 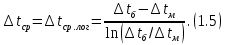 Если разности температур одинаковы или отличаются не более чем в два раза, то среднюю разность температур можно приближенно определить как среднеарифметическую: 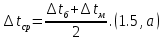 В многоходовых теплообменниках с простым смешанным током ∆tсрможно рассчитать по формуле: 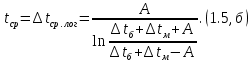 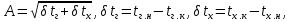 где tг.н,, tг.к. –начальная и конечная температура горячего теплоносителя; tх.н., хt.к. –начальная и конечная температура холодного теплоносителя; δtг, δtх – изменение температур. При изменении агрегатного состояния теплоносителя его температура постоянна вдоль всей поверхности теплопередачи и равна температуре кипения (или конденсации), зависящей от давления, состава теплоносителя. Коэффициент теплопередачи К, входящий в уравнение (1.1), можно рассчитать с помощью уравнения аддитивности термических сопротивлений на пути теплового потока: 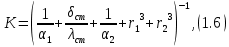 где α1, α2 – коэффициенты теплоотдачи со стороны теплоносителей; λст – теплопроводность стенки (Вт/(м·К)); δст – толщина стенки (м); 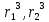 – термические сопротивления загрязнений с обеих сторон стенки ((м2·К)/Вт) [3, 4]. – термические сопротивления загрязнений с обеих сторон стенки ((м2·К)/Вт) [3, 4].Составление уравнения теплового баланса Решение задач управления, синтеза и анализа теплообменных процессов методами математического моделирования предполагает использование уравнения теплового баланса: приход тепла = расход тепла (статическая модель); накопление тепла = приход тепла – расход тепла (динамическая модель). Пусть задан расход более нагретого теплоносителя Gг, его энтальпия на входе аппарата Iг.н. и на выходе из аппарата Iг.к..Соответственно, расход более холодного теплоносителя – Gх, его начальная энтальпия Iх.н. и конечная –Iх.к.Тогда уравнение теплового баланса для установившегося (неизменного во времени) режима [1]: Q=Gг(Iг.н.–Iг.к.) = Gх(Iх.к.–Iх.н.) (1.7) Если теплообмен протекает без изменения агрегатного состояния теплоносителей, то энтальпии последних равны произведению теплоемкости с на температуру t (оС): Iг.н = cг.нtг.н, Iг.к = cг.кtг.к; Iх.н = cх.нtх.н, Iх.к = cх.кtх.к. (1.8) Величинысг.н.исг.к. представляют собой средние удельные теплоемкости более нагретого теплоносителя в пределах изменения температур от 0 до tг.н. (на входе в аппарат) и до tг.к.(на выходе из аппарата) соответственно;сх.н.исх.к. –средние удельные теплоемкости холодного теплоносителя в пределах 0 – tх.н. и 0 – tх.к. соответственно. Если теплообмен осуществляется при изменении агрегатного состояния теплоносителя (конденсация пара, испарение жидкости) или в процессе теплообмена протекают химические реакции, сопровождаемые тепловыми эффектами, то в тепловом балансе должно быть учтено тепло, выделяющееся при физическом или химическом превращении. Так, при конденсации насыщенного пара величина Iг.н. в уравнении (1.7) представляет собой энтальпию поступающего в аппарат пара, а Iг.к.–энтальпию удаляемого парового конденсата. В случае использования перегретого пара его энтальпия Iг.н.складывается из тепла, отдаваемого паром при охлаждении от температуры tг.н. до температуры насыщенияtгнас., тепла конденсации пара и тепла, выделяющегося при охлаждении конденсата: Q =Gг(Iг.н.– Iг.к.) =Gгcг.п.(tг.н. −tг.нас.)+Gгr+Gгcг.к.(tг.нас. – tг.к.), (1.9) где cг.п. и cг.к –удельные теплоемкости пара и конденсата;tг.к –температураконденсата на выходе. При обогреве насыщенным паром, если конденсат не охлаждается, т.е. tг.к = tг.н = tг.нас, первый и третий члены правой части уравнения (1.9) из теплового баланса исключаются. Для неустановившегося режима, когда наблюдается изменение температуры теплоносителя dt в интервале времени dτ, уравнения баланса для одного из теплоносителей, подаваемого в трубное пространство: dQ = Vρхcхdtх.к. = Gг(Iг.н.–Iг.к.)dτ–Gх (Iх.к.-Iх.н)dτ, где V – объем трубного пространства (м3), ρх – плотность нагреваемой среды (кг/м3). Преобразуем уравнение баланса и получим дифференциальное уравнение относительно температуры холодного теплоносителя на выходе аппарата: 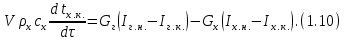 В качестве примера составим уравнение баланса для нагреваемой жидкости в трубном пространстве за малый промежуток времени dτ. В этом случае следует учесть: – теплоту, поступившую в теплообменник с жидкостью, dQ = Gхcхtх.н.dτ; – теплоту, полученную жидкостью от горячего теплоносителя через теплопередающую поверхность металлической стенки труб и затраченную на увеличение температуры жидкости tх.к., dQ = KF∆tсрdτ; – теплоту, уходящую с жидкостью из теплообменника,dQ = Gxcxtх.к.dτ; Тогда уравнение баланса имеет вид: 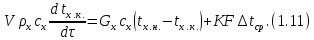 Расчет коэффициентов теплоотдачи Выбор уравнения для расчета коэффициентов теплоотдачи, используемых в уравнениях баланса, зависит от характера теплообмена (без изменения агрегатного состояния, кипение или конденсация), вида поверхности теплообмена, типа конструкции, режима движения теплоносителя [3, 4]. 1. При движениитеплоносителя в прямых трубах круглого сечения или в каналах некруглого сечения без изменения агрегатного состояния коэффициент теплоотдачи определяют по следующим уравнениям: 1.1. При развитом турбулентном движении (Re ≥104): 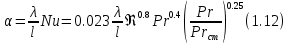 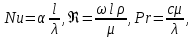 где Nu – критерий Нуссельта;Pr– критерий Прандтля; Prст– критерий Прандтля, рассчитанный при температуре стенки; ω – скорость (м/с). Определяющим размером l является эквивалентный диаметр (для труб круглого сечения – внутренний диаметр трубы dтвнутр(м)); определяющей температурой, при которой рассчитывают физические свойства среды, – средняя температура теплоносителя. Физические свойства: λ – теплопроводность; ρ – плотность; µ – динамическая вязкость (Па·с). 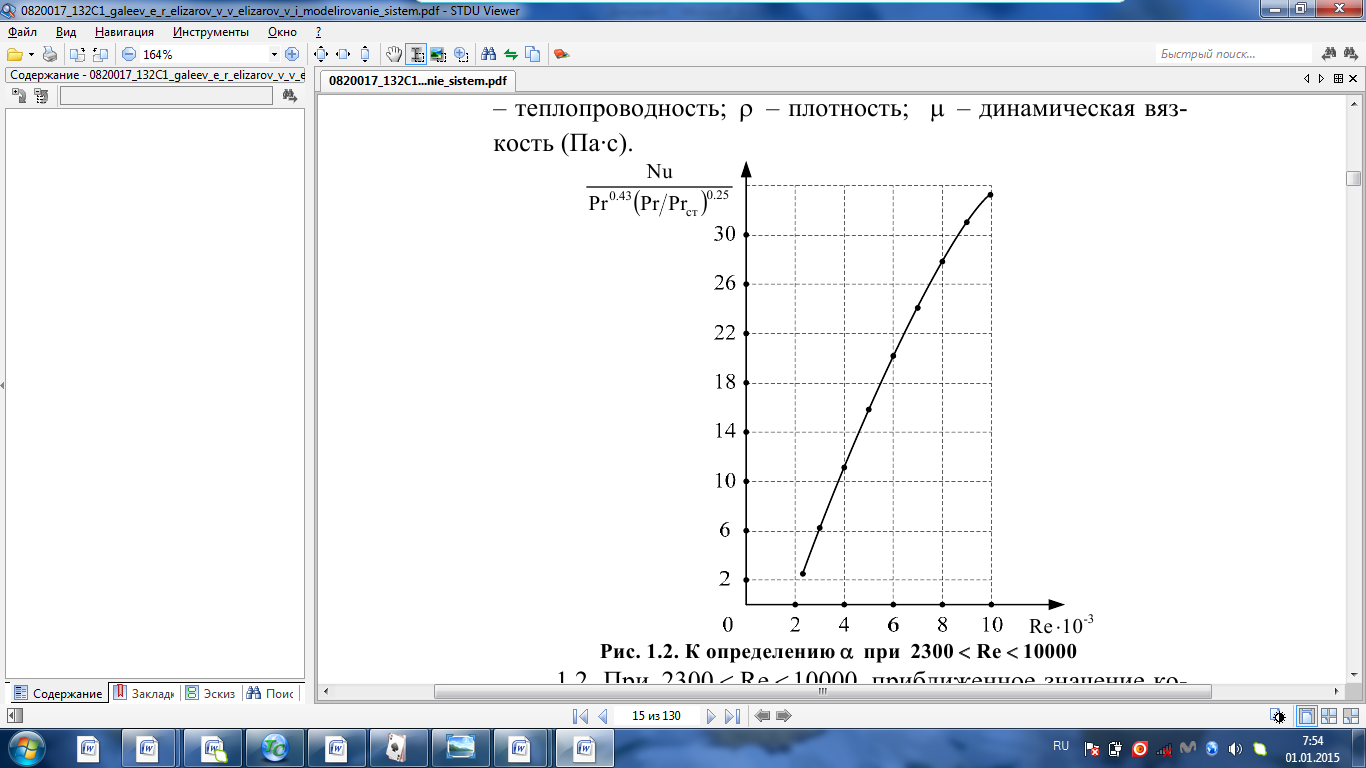 Рис. 1.2. К определению α при 2300 1.2. При 2300 1.3. В ламинарном режиме (Re ≤ 2300): а) при значениях 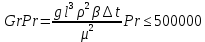 l (Gr – критерий Грасгофа, g – ускорение свободного падения (м/с2), β – коэффициент объемного расширения теплоносителя (1/град), ∆t – разность температур между стенкой и теплоносителем): l (Gr – критерий Грасгофа, g – ускорение свободного падения (м/с2), β – коэффициент объемного расширения теплоносителя (1/град), ∆t – разность температур между стенкой и теплоносителем):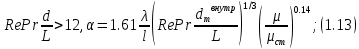 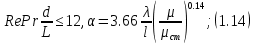 где µст – вязкость теплоносителя при температуре стенки; L – длина трубы (м); б) при значениях GrPr> 500000 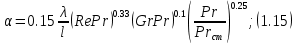 2. При движении теплоносителя в межтрубном пространстве с сегментными перегородками коэффициент теплоотдачи рассчитывают по уравнениям: 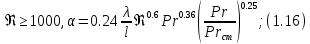 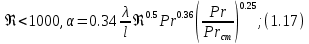 В уравнениях (1.16), (1.17) за определяющий геометрический размер принимают наружный диаметр теплообменных труб. Скорость потока определяют для площади сечения потока между перегородками [3]. 3. При конденсации пара на наружной поверхности пучка из n вертикальных труб коэффициент теплоотдачи: 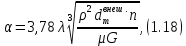 для n горизонтальных труб длиной L 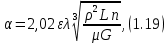 здесь dтвнеш. внешний диаметр трубы, ε = 0.7 при n ≤100 и ε= 0.6 при n> 100. Управление динамическими режимами работы теплообменного аппарата. Режимные параметры теплообменного оборудования являются переменными величинами как во времени, так и в пространстве. Такие параметры, как температуры теплоносителей в разных точках аппарата имеют различные значения. Основной причиной изменения параметров во времени является воздействия возмущений на аппарат в ходе его эксплуатации. В частности, отклонения входных параметров (расход, температура одного из теплоносителей) от проектных значений представляют собой возмущения на входе процесса. Наличие возмущений может привести к нарушению условий удовлетворительного функционирования аппарата, т.е. невыполнению требований по конечным температурам теплоносителей или их агрегатному состоянию. Для исключения таких ситуаций необходима система управления, реализованная на базе контрольно-измерительных приборов и ЭВМ. Управляющим параметром теплообменного аппарата, предназначенного для нагрева, охлаждения или конденсации одного из теплоносителей, является расход второго теплоносителя. Одним из способов определения значений управляющего параметра является расчет динамической модели процесса. Расчет модели проводится программным путем. Динамическая модель процесса состоит из дифференциальных уравнений, характеризующих изменение во времени температуры движущихся в теплообменнике сред, температуры теплопередающей стенки и др. [5]. Для решения уравнений могут использоваться численные методы. Рассмотрим работу теплообменного аппарата, предназначенного для нагревания технологического потока. Модель такого аппарата представлена дифференциальными уравнениями относительно температур tх.к. и tг.к. Соответствующие уравнения составляются аналитическими методами на основе фундаментальных законов сохранения тепла и по виду аналогичны уравнению (1.11). Расчет требуемого управления осуществляется системой управления (рис. 1.3). На основе измеренного значения Gх =Gх(τ) и первого приближения расхода Gг(τ) в начальный момент времени рассчитываются коэффициенты теплоотдачи α с учетом режима течения движущихся сред по одной из формул (1.12) – (1.19). По формуле (1.6) рассчитывается коэффициент теплопередачи К. Далее интегрируются дифференциальные уравнения. В конце временного такта проверяется условие равенства температуры нагреваемой смеси на выходе аппарата заданному значению. Если условие выполняется, то переходят к расчету на следующем временном такте, иначе выбирается новое приближение Gг(τ) в текущем такте. Пусть расход нагреваемой смеси на входе теплообменника заданной конструкции условно смоделирован в виде функций времени Gх = Gх(τ). Требуется найти расход нагревающего агента Gг(τ), при котором температура нагреваемой смеси на выходе аппарата равна заданной tзх.к. в дискретные моменты времени τ = k∆τ (k =1,2, 3...). 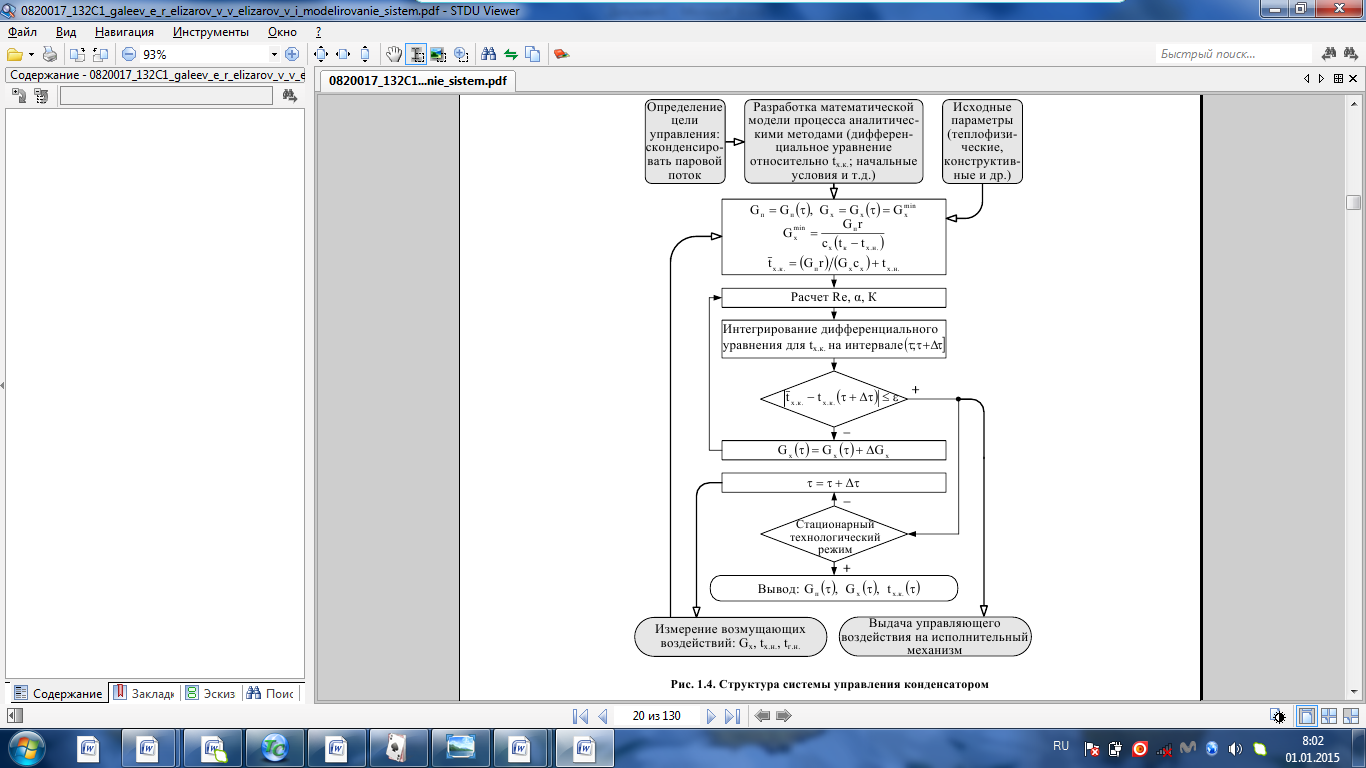 Рис. 1.4. Структура системы управления конденсатором При решении задачи управления конденсатором заданной конструкции, как правило, требуется определить расход охлаждающего агента Gx(τ) с начальной температурой tх.н., при котором полностью конденсируется паровая смесь. Возмущающими параметрами являются расход и температура паровой (газовой) смеси. Рассмотрим алгоритм поиска Gx(τ) (рис. 1.4) вдискретные моменты времени τ = k∆τ (k =1,2, 3...). Расход паровой смеси на входе теплообменника условно смоделирован в виде функции времени Gп = Gп(τ). Известна температура tк или давление конденсации паров. Т.к. температура одного из теплоносителей остается постоянной, то динамическую модель процесса представим уравнением относительно температуры охлаждающего агента на выходе аппарата tх.к..По своей структуре уравнение аналогично выражению (1.11). Температура конденсата постоянна и равна tк. Условием окончания поиска на каждом такте является равенство температуры охлаждающего агента на выходе, рассчитанной из уравнений динамики, температуре, определяемой балансовым соотношением: 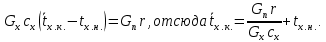 Начальные условия интегрирования дифференциальных уравнений задаются исходя из предположения о том, что аппарат до момента возникновения возмущений функционировал удовлетворительно. В этом случае: 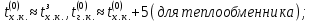 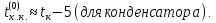 Процедура поиска управления продолжается до достижения теплообменным аппаратом стационарного (установившегося) режима работы, при котором состояние входа и выхода аппарата неизменны во времени. Результаты моделирования 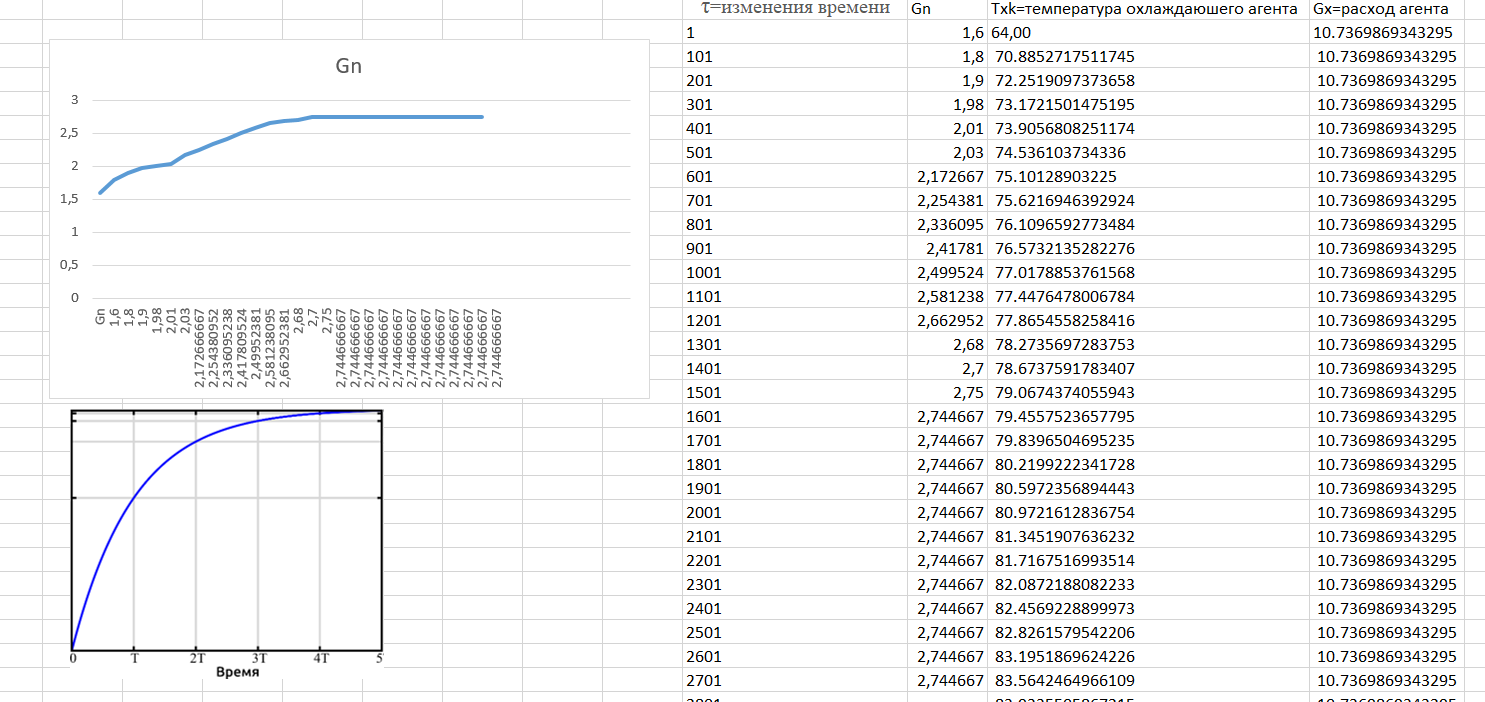 В результате построения динамической модели системы управления конденсатором на основе анализа уравнения динамики процесса 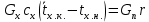 были найдены, Оптимальные значения расхода охлаждающего агента-(Gn=2.7 кг/с). Расхода паров-(Gx=10.736986… кг/с). Также время пребывания их в теплообменном аппарате-(τ=1401c). Конечный температура охлаждающего агента-( Txk=92.1835587628536 C’) Приложение const PI = 3.141592654; e = 2.17; Tk = 64; Txn = 23; r = 1150000; Cx = 4180; dt = 0,05; n = 196; z = 6; mx = 0.00082; mk = 0.0000446; lamda = 0.218; F = 46; eps = 0.6; px = 780; Dm=0.6 label rollback1, rollback2; var p, mg, D_t, Gx, Gn, Gxmin, Txk2: real; Txk1, Tx, Re, a, K, t, deltat, At: real; function Gn_f(tau: real):real; var h: real; begin if tau<=3600 then result:=Power(tau, 0.05)+Power(e, tau/8500)-0.4 else result:=2.7; end; function integral(a,b: real):real; var x,h,s:real; function Y(t:real):real; begin Y:=K*F*((Tk+Txn)/2); end; begin h:=(b-a)/1000; s:=0; x:=a+h; while x begin s:=s+4*Y(x); x:=x+h; s:=s+2*Y(x); x:=x+h; end; s:=h/3*(s+Y(a)-Y(b)); writeln; result:=s; end; begin t := 1; deltat :=100 ; Gxmin:=(Gn_f(t)*r)/(Cx*(Tk-Txn)); Gx := Gxmin; rollback2: Gn := Gn_f(t); Txk2:=(Gn*r)/(Gx*Cx)+Txn; rollback1: writeln('Gn = ',Gn_f(t)); writeln('Gx = ',Gx); writeln('txk = ',txk2); Re:=(4*Gx)/(PI*dt*(n/z)*mx); a:=3.78*lamda*Power((Power(px,2)*dt)/(mk*Gn),1/3); K:=1/(1/a+0.045/50+1/5000); Txk1 := integral(t,t+deltat); if(abs(Txk2-Txk1*(t + deltat))>=eps) then begin if(Gn=2.7) then begin writeln('Gn = ',Gn_f(t)); writeln('Gx = ',Gx); writeln('txk = ',txk2); read(T); end else begin t := t + deltat; goto rollback2; end; end else begin Gx := Gx + 1; goto rollback1; end; end. Заключение В данной курсовой работы была смоделирована система управления конденсатором на основе анализа уравнений динамики процесса, исследован процесс функционирования кожухотрубного конденсатора, определен расход охлаждающего агента (воды), определена зависимость значения расхода охлаждающего агента, расхода паров, а также температуры охлаждающего агента на выходе аппарата от времени c использованием языка программирования Pascalabc. Список литературы 1. Ченцова,Л.И. Процессы и аппараты химической технологии: учебное пособие к самостоятельной работе/ Л.И. Ченцова, М.К. Шайхудинова, В.М. Ушанова.- Красноярск: СибГТУ,2006.-267с. 2. Основные процессы и аппараты химической технологии: Пособие по проектированию/ Г.С. Борисов, В.П. Брыков, Ю.И. Дытнерский и др. Под ред. Ю.И. Дытнерского, 2-е изд., перераб. и дополн. М.: Химия, 1991. – 496 с. 3. Павлов, К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии: Учебное пособие для вузов. Перепечатка с изд. 1987г.- М.: ООО «РусМедиаКонсалт», 2004.-576с. 4. Левин Б.Д., Ченцова Л.И., Шайхутдинова М.Н., Ушанова В.М. процессы и аппараты химических и биологических технолгий. Учеб. пособие для студентов химических специальностей вузов / Под общ. ред. д-ра. хим. Наук С.М. Репяха. – Красноярск: Сибирский государственный технологический университет, 2002. - 430с. 5. Шайхудинова М.К., Ченцова Л.И., Борисова Т.В. Процессы и аппараты химической технологии. Расчет выпарной установки: учебное пособие к выполнению курсового проекта.-Красноярск: СибГТУ, 2005.- 80с. 6. Конструкции теплообменников (ifmo.ru) |