крТА. Курсовая работа по предмету "прикладная теория цифровых автоматов" Студент Рахмуков В. В

• Название: Курсовая работа по предмету "прикладная теория цифровых автоматов" Студент Рахмуков В. В
• Дата: 22.01.2022
• Размер: 156.03 Kb.
• Имя файла: 213741-91020.docx
• Тип: Курсовая; #338490
• страница: 2 из 5

Интерфейс вычислителя

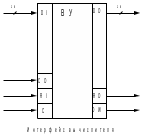
DI [0-15]	входная 16- разрядная информационная шина для приёма операндов
D0 [0-15]	выходная 16- разрядная информационная шина для выдачи результата
RI	входной сигнал готовности : если RI = 1, то данные на шине DI готовы для считывания
RO	выходной сигнал готовности : если RO=1, то готов результат на шине DO
CO	код операции : если CO=1, то выполняется операция сложения с фиксированной точкой, если СО=0, то выполняется операция вычитания с плавающей точкой
OW	Сигнал переполнения разрядной сетки автомата если OW=1, то имеется переполнение
C	синхронизация

5. Математическое обоснование используемых алгоритмов

Проектируя алгоритм вычислений будем исходить из следующих утверждений

• 
  Сумма дополнительных кодов чисел есть дополнительный код результата
  
• 
  Сложение и вычитание производим в модифицированном дополнительном коде
  
• 
  Признаком переполнения разрядной сетки сумматора дополнительного кода при сложении положительных чисел является отрицательный знак результата, а при сложении отрицательных чисел положительный знак результата
  
• 
  Признаком нарушения нормализации числа справа ( когда величина результата равна или превышает единицу ) является наличие разноимённых комбинаций в знаковых разрядах сумматора
  
• 
  Признаком нарушения нормализации числа слева ( когда результат по абсолютной величине оказывается меньше 1/q ) является наличие одинаковых комбинаций в разряде переполнения и старшем разряде цифровой части сумматора
  
• 
  Вычитание с плавающей точкой выполняем на сумматоре инвертировав знак мантиссы
  

6. Типовые примеры

Сложение с фиксированной точкой
Aдоп=0.101000010001101 Bдоп=0.010000100010010
0	1		2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
0	0		1	0	1	0	0	0	0	1	0	0	0	1	1	0	1	RgA
0	0		0	1	0	0	0	0	1	0	0	0	1	0	0	1	0	RgB
0	0		1	1	1	0	0	0	1	1	0	0	1	1	1	1	1	Сумма
знаковые разряды одинаковы, переполнения нет, результат верен
Aдоп=0.101110000010001 Bдоп=0.110110000010101
0	0		1	0	1	1	1	0	0	0	0	0	1	0	0	0	1	RgA
0	0		1	1	0	1	1	0	0	0	0	0	1	0	1	0	1	RgB
0	1		1	0	0	1	0	0	0	0	0	1	0	0	1	1	0	Сумма
знаковые разряды разные, имеется переполнение разрядной сетки, результат неверен
Aдоп=-.010100000000000 Bдоп=-.011100000000000
1	1		0	1	0	1	0	0	0	0	0	0	0	0	0	0	0	RgA
1	1		0	1	1	1	0	0	0	0	0	0	0	0	0	0	0	RgB
1	0		1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	Сумма
знаковые разряды разные, имеется переполнение разрядной сетки, результат неверен
Aдоп=-.111110000000000 Bдоп=-.111110000000000
1	1		1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	RgA
1	1		1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	RgB
1	1		1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	Сумма
знаковые разряды одинаковые, но имеется перенос в старший разряд, следовательно возникло переполнение разрядной сетки, результат неверен
Вычитание с плавающей точкой
Aдоп=0.100000000 * 2-3 Bдоп=0.010100000 * 2-3
0	0		1	0	0	0	0	0	0	0	0	1	1	1	1	0	1	RgA
1	1		0	1	0	1	0	0	0	0	0	1	1	1	1	0	1	RgB
1	1		1	1	0	1	0	0	0	0	0	1	1	1	1	0	1	Суммируем мантиссы
1	1		1	0	1	0	0	0	0	0	0	1	1	1	1	0	0	нормализация влево
1	1		0	1	0	0	0	0	0	0	0	1	1	1	0	1	1	нормализация влево
1	1		0	1	0	0	0	0	0	0	0	1	1	1	0	1	1	результат
Aдоп= -.011000000 * 22 Bдоп= -.111000000 * 25
1	1		0	1	1	0	0	0	0	0	0	0	0	0	0	1	0	RgA
0	0		1	1	1	0	0	0	0	0	0	0	0	0	1	0	1	RgB
1	1		1	0	1	1	0	0	0	0	0	0	0	0	0	1	1	выравнивание порядков
1	1		1	1	0	1	1	0	0	0	0	0	0	0	1	0	0	выравнивание порядков
1	1		1	1	1	0	1	1	0	0	0	0	0	0	1	0	1	выравнивание порядков
0	0		1	1	0	0	1	1	0	0	0	0	0	0	1	0	1	Суммируем мантиссы
0	0		1	1	0	0	1	1	0	0	0	0	0	0	1	0	1	результат