Учебник авт. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир Диктант 1 по теме Цифры. Десятичная запись натуральных чисел
 Скачать 341.68 Kb. Скачать 341.68 Kb.
|
|
Математические диктанты по математике (5 класс, учебник авт. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир) Диктант 1 по теме «Цифры. Десятичная запись натуральных чисел» 1. Запишите цифрами число: 1) двести тридцать семь тысяч сто пять; 2) двадцать девять тысяч двадцать; 3) десять миллиардов десять миллионов один; 4) сто пять миллионов семьдесят пять тысяч; 5) девяносто миллионов четыреста шесть тысяч двенадцать; 6) шестьсот двадцать миллиардов восемнадцать миллионов девятьсот тысяч восемьсот сорок. 2. Запишите словами число: 1) 202 201; 3) 2 200 021; 5) 2 000 020 002; 2) 220 021; 4) 2 020 202 020; 6) 20 000 200 002. 3. Какая цифра в числе 465 321 598 702 стоит в разряде: 1) сотен; 3) сотен миллионов; 2) сотен тысяч; 4) сотен миллиардов? 4. Какое число записано в виде суммы разрядных слагаемых: 1) 80 000 + 6 000 + 300 + 50 + 8; 2) 9 000 000 + 700 000 + 5 000 + 2; 3) 1 000 000 000 + 30 000 + 100 + 9; 4) 500 000 + 5 000 + 50? 5. Запишите: 1) наибольшее двузначное число; 2) наименьшее четырёхзначное число; 3) наибольшее четырёхзначное число; 4) наименьшее шестизначное число; 5) наибольшее семизначное число. 6. Запишите все двузначные натуральные числа, сумма цифр которых равна 5. 7. Запишите три первых трёхзначных числа, сумма цифр которых равна 3. 8. Запишите цифрами и словами шестизначное число, у которого в разряде десятков тысяч стоит цифра 5, в разряде сотен — цифра 2, а все остальные цифры — тройки. 9. Какое наибольшее и какое наименьшее четырёхзначные числа можно записать, используя по одному разу цифры 0, 2, 6 и 8? Д  иктант 2 по теме «Отрезок. Длина отрезка» иктант 2 по теме «Отрезок. Длина отрезка»1. Сколько отрезков изображено на рисунке 3? 2. Точка P лежит на отрезке CM. Запишите все отрезки, на которые точка P делит отрезок CM. 3. Начертите отрезок AB и отметьте на нём точки M, K и P так, чтобы точка M лежала между точками K и P. 4. Начертите отрезки AB и CD так, чтобы: 1) они пересекались; 2) они не пересекались; 3) отрезок CD лежал на отрезке AB; 4) только точка A отрезка AB лежала на отрезке CD. 5. Укажите среди данных отрезков равные, если AB = 4 см 8 мм, CD = 3 м 6 см, EF = 36 см, MK = 5 дм 4 мм, NP = 48 мм, ST = 504 мм. 6. Начертите какую-нибудь ломаную, состоящую из трёх звеньев. 7. Какова длина ломаной CDEF, если CD = 8 мм, DE = 10 мм и EF = 14 мм? 8  . Ломаная состоит из двух звеньев длиной 28 мм и 2 см. Какова длина ломаной? . Ломаная состоит из двух звеньев длиной 28 мм и 2 см. Какова длина ломаной? 9. На отрезке AC отметили точку B (рис. 4). Чему равна длина отрезка AC, если расстояние между серединами отрезков AB и BC составляет 10 см? Диктант 3 по теме «Плоскость. Прямая. Луч» 1 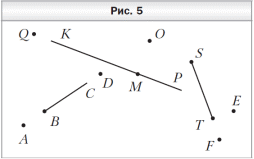 . Запишите, какие из точек A, D, O, M, B, S, T, E, F, Q (рис. 5) принадлежат: . Запишите, какие из точек A, D, O, M, B, S, T, E, F, Q (рис. 5) принадлежат: 1) прямой KP; 2) лучу BC; 3) отрезку ST. 2. Пересекаются ли изображённые на рисунке 5: 1) луч BC и прямая KP; 2) прямая KP и отрезок ST; 3) луч BC и отрезок ST? 3. Запишите все отрезки и лучи, изображённые на рисунке 6. 4. Начертите произвольную прямую a и отметьте на ней точки C, D и E так, чтобы точка E лежала между точками C и D. Запишите: 1) все возможные обозначения прямой a с использованием точек C, D и E; 2) все лучи, началом которых является точка E. 5  . Сколько лучей изображено на рисунке 7? . Сколько лучей изображено на рисунке 7?Диктант 4 по теме «Шкала. Координатный луч» 1. Закончите предложение. 1) Если на луче с началом в точке O отложить отрезок OA и под точкой O подписать число 0, а под точкой A — число 1, то отрезок OA называют …. 2) Если единичный отрезок отложить от начала координатного луча 6 раз, то концу шестого отрезка соответствует число …. 3) Если точке B на координатном луче соответствует число 12, то это записывают так: …. 4) Если на координатном луче от точки C с координатой 28 вправо отложить единичный отрезок CD, то точке D будет соответствовать число …. 5) Если на координатном луче от точки E с координатой 40 влево отложить единичный отрезок EF, то точке F будет соответствовать число …. 2. Запишите, каким числам соответствуют точки A, B, C, D, E, F на рисунке 8.  3. Сколько единичных отрезков надо отложить от начала координатного луча, чтобы отметить на нём число: 1) 7; 2) 1 364; 3) 1 000 000? 3. Сколько единичных отрезков надо отложить от начала координатного луча, чтобы отметить на нём число: 1) 7; 2) 1 364; 3) 1 000 000? 4. Запишите все однозначные числа, которые на координатном луче расположены правее числа 5. 5. Какое число стоит на координатном луче рядом с числом 2 736: 1) справа от него; 2) слева от него? 6. Запишите все натуральные числа, которые расположены на координатном луче между числами 2 508 и 2 515. 7. Какую координату имеет точка M, если: 1) она лежит между точками A (27) и B (29); 2) она является серединой отрезка CD, где C(0) и D(56)? 8. На шкале отметили числа от 0 до 50. Возле каждого штриха стоит одно число. Сколько делений между штрихами, возле которых стоят числа: 1) 2 и 7; 2) 8 и 18; 3) 19 и 45? Диктант 5 по теме «Сравнение натуральных чисел» 1. Запишите неравенство: 1) девять меньше двенадцати; 2) десять больше 6; 3) число a меньше числа b. 2. Запишите, как читается двойное неравенство 4 < 7 < 8. 3. Сравните числа: 1) 483 и 501; 2) 970 и 1 005; 3) 1 024 и 1 204. 4. Запишите все натуральные числа, которые больше 14, но меньше 18. 5. Запишите четырёхзначное число, которое меньше, чем 1 017, и оканчивается цифрой 7. 6. Запишите наименьшее натуральное число, которое можно подставить вместо m в неравенство m > 734, чтобы это неравенство было верным. 7. Запишите наибольшее натуральное число, которое можно подставить вместо n в неравенство n < 3 108, чтобы это неравенство стало верным. 8. Какие натуральные числа можно поставить вместо звёздочки, чтобы получилось верное неравенство: 1) * + 42 < 51; 2) 25 < * + 14 < 29? Диктант 6 по теме «Сложение натуральных чисел. Свойства сложения» 1. Закончите предложение. 1) Число, получаемое в результате сложения двух чисел, называют …. 2) Числа, которые складывают, называют …. 3) От перестановки слагаемых сумма …. 4) Для чисел c и d переместительное свойство сложения записывают так: …. 5) Чтобы к сумме двух чисел прибавить третье число, можно …. 6) Для чисел m, n и p сочетательное свойство сложения записывают так: …. 7) Сумма двух первых трёхзначных чисел равна …. 8) Число 3 можно записать в виде суммы двух натуральных чисел так: …. 9) Если число 156 увеличить на 44, то получим …. 10) Если число 9 998 увеличить на 12, то получим …. 11) Сумма наименьшего трёхзначного числа и наименьшего четырёхзначного числа равна …. 12) Сумма числа 7 458 и числа 0 равна …. 13) Если сумму чисел 16 и 25 увеличить на 35, то получим …. 2. Сумма двух слагаемых оканчивается цифрой 6. Какими цифрами могут заканчиваться слагаемые? 3. Сумма двух чисел больше одного из них на 164. Чему равно второе число? 4. Выполните сложение: 1) (7 + 69) + 31; 3) 14 + 19 + 26 + 21; 2) 14 + (79 + 186); 4) 78 + 43 + 57 + 22. 5. Упростите выражение: 1) (12 + m) + 18; 3) 51 + a + 29; 2) 14 + (n + 36); 4) b + 193 + 207. 6. Как изменится сумма двух чисел, если: 1) одно из слагаемых увеличить на 100; 2) каждое из слагаемых уменьшить на 100? Диктант 7 по теме «Вычитание натуральных чисел» 1. Закончите предложение. 1) Число, получаемое в результате вычитания одного числа из другого, называют …. 2) Число, из которого вычитают другое число, называют …. 3) Число, которое вычитают из другого числа, называют …. 4) Если a + b = c, то b = …. 2. Запишите в виде равенства, что число a больше числа c на 58. 3. Чему равна разность: 1) 248 − 248; 2) 156 − 0? 4. На сколько: 1) число 78 больше числа 42; 2) число 29 меньше числа 55? 5. Найдите разность между четырёхзначным и трёхзначным числами, для записи которых используется только цифра 1. 6. Разность меньше уменьшаемого на 19. Чему равно вычитаемое? 7. В 5 классе учатся 22 мальчика, что на 9 больше, чем девочек. Сколько всего учащихся в этом классе? 8. Уменьшаемое увеличили на 20. Как надо изменить вычитаемое, чтобы разность: 1) увеличилась на 20; 2) уменьшилась на 20; 3) не изменилась? 9. В четырёхзначном числе отбросили первую слева цифру 4. Как изменилось, увеличилось или уменьшилось, это число и на сколько? 10. К пятизначному числу дописали слева цифру 5. Как изменилось, увеличилось или уменьшилось, это число и на сколько? Диктант 8 по теме «Числовые и буквенные выражения. Формулы» 1. Запишите в виде выражения: 1) разность чисел 48 и 29; 2) сумму чисел 127 и 463; 3) произведение чисел 502 и 10 300; 4) частное чисел 2 052 и 18. 2. Запишите разность чисел x и 12, найдите значение этой разности при x = 21. 3. Сумму чисел 18 и 12 увеличьте в 5 раз. 4. Разность чисел 82 и 46 увеличьте на 14. 5. Произведение чисел 18 и 4 уменьшите на 50. 6. Частное чисел 96 и 16 уменьшите в 6 раз. 7. Чему равно значение выражения 2x − 7, если x = 9? 8. В вазе a красных и b белых гвоздик. Составьте выражение для нахождения количества гвоздик в вазе. Вычислите значение полученного выражения, если: 1) a = 12; b = 16; 2) a = 20; b = 17. 9. Найдите по формуле пути s = vt значение скорости v, если t = 4 ч, s = 36 км. 10. Книга стоит m р., тетрадь — n р., причём тетрадь на 62 р. дешевле книги. Запишите формулу, по которой можно вычислить цену книги, если известна цена тетради. Диктант 9 по теме «Уравнение» 1. Закончите предложение. 1) Корнем уравнения называют значение переменной, при котором …. 2) Решить уравнение означает …. 3) Чтобы найти неизвестное слагаемое, надо …. 4) Чтобы найти неизвестное вычитаемое, надо …. 5) Чтобы найти неизвестное уменьшаемое, надо …. 2. К какому числу надо прибавить 18, чтобы получить 50? 3. Из какого числа надо вычесть 14, чтобы получить 26? 4. Какое число надо вычесть из 80, что бы получить 35? 5. Запишите корень уравнения: 1) x + 13 = 28; 2) 20 − x = 12; 3) x − 11 = 79. 6. При каком значении a выполняется равенство: 1) a + 10 = 10 + a; 2) a − 10 = 10 − a? 7. Составьте уравнение: 1) корнем которого является число 2; 2) не имеющее корней; 3) корнем которого является любое число. 8. Угадайте корень уравнения: 1) 100x = 10x; 3) x : 2 + 5 = x; 2) x + x = x ⋅ x; 4) 10 − x ⋅ x = 1. Диктант 10 по теме «Угол. Обозначение углов» 1 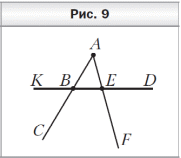 . Запишите пары лучей (рис. 9), имеющих общее начало. . Запишите пары лучей (рис. 9), имеющих общее начало. 2. Закончите предложение. 1) Углом называют фигуру, образованную …. 2) Два угла называют равными, если …. 3) Луч, выходящий из вершины угла и делящий его на два равных угла, называют …. 3. Запишите все возможные обозначения угла со сторонами DA и DC. 4. Какие лучи являются сторонами угла ACM? 5. Какая точка является вершиной угла OMB? 6. Запишите углы, изображённые на рисунке 10.  7. Начертите угол MOK и отметьте: 7. Начертите угол MOK и отметьте: 1) точки A и B на разных сторонах угла; 2) точки C и D на одной стороне угла; 3) точку E внутри угла; 4) точку F вне угла. 8. Запишите, используя обозначения, что угол ABC равен углу DMK. Диктант 11 по теме «Виды углов. Измерение углов» 1. Закончите предложение. 1) Развёрнутым называют угол, стороны которого …. 2) Градусная мера развёрнутого угла равна …. 3) Прибор, используемый для измерения углов, называют …. 4) Равные углы имеют равные …. 5) Из двух неравных углов большим считают тот, …. 6) Острым называют угол, градусная мера которого …. 7) Прямым называют угол, градусная мера которого …. 8) Тупым называют угол, градусная мера которого …. 9) Биссектриса развёрнутого угла делит его на …. 2. Запишите, используя обозначения: градусная мера угла CDE равна 46°. 3. Определите вид каждого из следующих углов: ∠A = 80°; ∠B = 180°; ∠C = 102°; ∠D = 91°; ∠E = 40°; ∠F = 90°. 4. Начертите острый угол ABC. 5. Начертите тупой угол MDP. 6. С помощью транспортира постройте угол, градусная мера которого равна 80°, и проведите его биссектрису. 7. Укажите все острые и тупые углы, изображённые на рисунке 11. 8. На рисунке 12 ∠ABD =∠CBF = 50°. Вычислите величины угла DBF и угла ABF. 9. Укажите вид и градусную меру угла, который образуют минутная и часовая стрелки часов: 1) в 9 ч; 2) в 18 ч; 3) в 22 ч; 4) в 16 ч. 10. Запишите все пары углов, изображённых на рисунке 13, сумма градусных мер которых равна 180°. 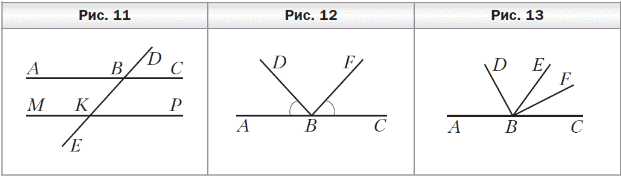 11. Два угла, градусные меры которых равны 40° и 60°, имеют общую сторону. Чему равен угол между биссектрисами этих углов? 11. Два угла, градусные меры которых равны 40° и 60°, имеют общую сторону. Чему равен угол между биссектрисами этих углов?Диктант 12 по теме «Треугольник и его виды» 1. Закончите предложение. 1) Тупоугольным называют треугольник, у которого …. 2) Прямоугольным называют треугольник, у которого …. 3) Остроугольным называют треугольник, у которого …. 4) Разносторонним называют треугольник, у которого …. 5) Равнобедренным называют треугольник, у которого …. 6) Равносторонним называют треугольник, у которого …. 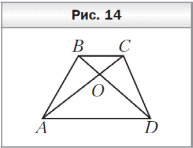 2. Определите вид треугольника BCE, если ∠B = 40°, 2. Определите вид треугольника BCE, если ∠B = 40°, ∠C = 95°, ∠E = 45°. 3. Определите вид треугольника DKP, если DK = 32 мм, KP = 32 см, DP = 3 дм 2 см. 4. Сколько треугольников изображено на рисунке 14? 5. На рисунке 15 изображены треугольники, длины сторон которых выражены в сантиметрах. Найдите периметр: 1) равностороннего треугольника; 2) тупоугольного равнобедренного треугольника; 3) прямоугольного разностороннего треугольника; 4) остроугольного разностороннего треугольника; 5) остроугольного равнобедренного треугольника; 6) тупоугольного разностороннего треугольника. 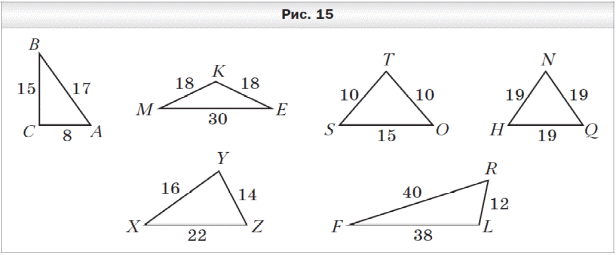 6. Определите вид треугольника, две стороны которого равны 9 см и 12 см, а периметр — 30 см. 7. Найдите периметр равностороннего треугольника, если он на 26 см больше его стороны. Диктант 13 по теме «Прямоугольник» 1. Закончите предложение. 1) Прямоугольником называют четырёхугольник, у которого …. 2) Соседними называют стороны прямоугольника, имеющие …. 3) Соседние стороны прямоугольника называют его …. 4) Стороны прямоугольника, которые не имеют общих вершин, называют …. 5) Если длина прямоугольника равна a, а ширина — b, то его периметр вычисляют по формуле …. 6) Квадратом называют прямоугольник, у которого …. 2. Каждая сторона прямоугольника равна 9 см. 1) Как называют такой прямоугольник? 2) Чему равен его периметр? 3. Чему равна сумма всех углов квадрата? 4. Сколько прямоугольников изображено на рисунке 16? 5. Четырёхугольники ADEB, BEFC, EKMF — квадраты со стороной 4 см (рис. 17). 1) Вычислите периметр многоугольника ADEKMC. 2) Биссектрисой каких углов является луч CE? 6. Вычислите периметр прямоугольника, одна из сторон которого равна 26 см, что на 12 см больше длины другой стороны. 7. Чтобы натянуть сетку вокруг участка, имеющего форму квадрата, вдоль каждой стороны надо поставить 10 столбиков. Сколько всего требуется столбиков? 8. Сколько квадратов изображено на рисунке 18? Сколько прямоугольников, отличных от квадрата, изображено на этом рисунке? 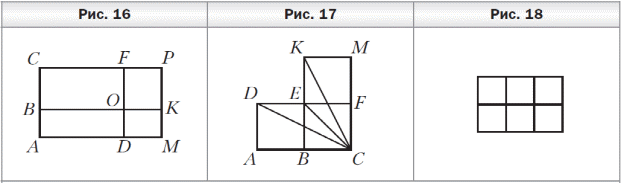 Диктант 14 по теме «Умножение. Переместительное свойство умножения» 1. Закончите предложение. 1) Число, получаемое в результате умножения двух чисел, называют …. 2) Числа, которые умножают, называют …. 3) От перестановки множителей произведение …. 4) Для чисел m и n переместительное свойство умножения записывают так: …. 5) Произведение чисел 761 и 0 равно …. 6) Произведение чисел 128 и 1 равно …. 7) Произведение двух чисел равно нулю, если …. 8) Произведение двух чисел равно одному из множителей, если …. 2. Запишите в виде суммы равных слагаемых произведение 19 ⋅ 4. 3. Запишите в виде произведения сумму 13 + 13 + 13 + 13 + 13 + 13 + 13. 4. Найдите: 1) сумму трёх слагаемых, каждое из которых равно 5; 2) произведение трёх множителей, каждый из которых равен 5. 5. Мотоциклист едет со скоростью 72 км/ч. Какое расстояние он проедет за: 1) 3 ч; 2) 5 ч? 6. Килограмм конфет стоит 80 р. Сколько надо заплатить за: 1) 4 кг конфет; 2) 9 кг конфет? 7. Вычислите: 1) 103 ⋅ 5; 3) 406 ⋅ 8; 5) 602 ⋅ 20; 2) 204 ⋅ 3; 4) 805 ⋅ 9; 6) 7 080 ⋅ 40. 8. Запишите число, которое: 1) в 3 раза больше числа 1 025; 2) в 6 раз больше наименьшего семизначного числа. 9. Произведение двух чисел в 9 раз больше одного из множителей и в 12 раз больше второго множителя. Чему равно произведение? 10. Какими цифрами могут оканчиваться два числа, если их произведение оканчивается цифрой: 1) 5; 2) 6? 11. Решите уравнение (8 − x)(x − 2) = 0. Диктант 15 по теме «Сочетательное и распределительное свойства умножения» 1. Запишите в буквенном виде равенство, выражающее: 1) сочетательное свойство умножения; 2) распределительное свойство умножения относительно сложения; 3) распределительное свойство умножения относительно вычитания. 2. Вычислите наиболее удобным способом: 1) 25 ⋅ 78 ⋅ 4; 4) 49 ⋅ 9 + 21 ⋅ 9; 2) 2 ⋅ 49 ⋅ 50; 5) 316 ⋅ 5 − 216 ⋅ 5. 3) 3 ⋅ 5 ⋅ 8 ⋅ 3; 6) 239 ⋅ 47 + 239 ⋅ 53. 3. Упростите выражение: 1) 2 ⋅ x ⋅ 15; 3) 27x − 19x; 2) 6 ⋅ a ⋅ 13 ⋅ b; 4) 32y − 14y + y. 4. Верно ли неравенство: 1) 5 ⋅ 324 ⋅ 20 < 4 ⋅ 323 ⋅ 25; 2) 63 ⋅ 50 > 5 ⋅ 7 ⋅ 9 ⋅ 5 ⋅ 2; 3) 2 ⋅ 2 ⋅ 5 ⋅ 57 ⋅ 5 > 5 ⋅ 56 ⋅ 20; 4) 14 ⋅ 3 ⋅ 25 ⋅ 5 ⋅ 8 < 7 ⋅ 3 ⋅ 3 ⋅ 10 ⋅ 25 ⋅ 4? Диктант 16 по теме «Деление» 1. Закончите предложение. 1) Число, получаемое в результате деления двух чисел, называют …. 2) Число, которое делят на другое число, называют …. 3) Число, на которое делят, называют …. 4) Если a : b = c, то a = …. 5) Если m : n = k, то n = …. 6) Чтобы найти неизвестный множитель, надо …. 7) Чтобы найти неизвестный делитель, надо …. 8) Чтобы найти неизвестное делимое, надо …. 9) Частное чисел 0 и 456 равно …. 10) Частное чисел 250 и 1 равно …. 11) Частное чисел 214 и 214 равно …. 12) Нельзя выполнить деление на число …. 2. Выполните деление: 1) 318 : 3; 2) 408 : 4; 3) 4 200 : 7; 4) 1 200 : 60. 3. Запишите выражение и найдите его значение: 1) частное произведения чисел 12 и 4 и числа 9; 2) частное суммы и разности чисел 180 и 140. 4. Какое число надо умножить на 5, чтобы получить 90? 5. Какое число надо разделить на 20, чтобы получить 10? 6. На какое число надо разделить 164, чтобы получить 41? 7. Какое число: 1) в два раза меньше, чем 10 000; 2) в три раза меньше, чем 9 090 909? 8. Делимое в 17 раз больше частного. Чему равен делитель? 9. Делитель в 23 раза меньше делимого. Чему равно частное? 10. Делимое увеличили в 7 раз. Что надо сделать с делителем, чтобы частное: 1) не изменилось; 2) уменьшилось в 2 раза; 3) увеличилось в 21 раз? 11. Запишите корень уравнения: 1) 7x − x = 624; 2) 7x + 12 = 47; 3) 65 : (x − 4) = 13. 12. Чему равно значение выражения, где a — некоторое отличное от 0 число: 1) a : 1 + 0 : a; 2) a ⋅ 1 − a : 1; 3) (1 ⋅ a − 1) ⋅ 0? Диктант 17 по теме «Деление с остатком» 1. При делении числа 54 на 5 получаем остаток …. 2. При делении числа 44 на 7 неполным частным является число …. 3. Запишите все остатки, которые могут получиться при делении различных чисел на 7. 4. Найдите делимое, если делитель равен 4, неполное частное — 8, остаток — 3. 5. Найдите неполное частное и остаток при делении: 1) 48 на 10; 2) 49 на 9; 3) 90 на 11; 4) 38 на 12. 6. Блокнот стоит 15 р. Какое наибольшее количество блокнотов можно купить, имея 100 р.? 7. Чему равен остаток при делении числа 543 276: 1) на 10; 2) на 100; 3) на 1 000 ? 8. При каком наименьшем натуральном значении a при делении значения выражения a + 47 на число 10 остаток равен 3? Диктант 18 по теме «Площадь. Площадь прямоугольника» 1. Чему равна площадь прямоугольника со сторонами 20 дм и 4 м? 2. Чему равна площадь квадрата, периметр которого равен 36 см? 3. Найдите периметр квадрата, площадь которого равна 49 м2. 4. Какова длина стороны квадрата, площадь которого равна 1 га? 5. Сколько квадратных метров содержится в 4 а? 6. Сколько квадратных сантиметров содержится в 2 дм2 4 см2? 7. Скольким арам равна площадь участка, длина которого 40 м, а ширина — 25 м? 8. Верно ли утверждение: 1) если две фигуры равны, то их площади равны; 2) если площади двух фигур равны, то эти фигуры равны; 3) если два квадрата имеют равные площади, то они равны; 4) если два прямоугольника имеют равные периметры, то их площади равны? 9. Запишите окончание предложения. 1) Измерить площадь фигуры — значит подсчитать, сколько в ней помещается …. 2) Площадь прямоугольника равна произведению …. 3) Площадь квадрата, сторона которого равна a, вычисляют по формуле …. Диктант 19 по теме «Прямоугольный параллелепипед. Пирамида» 1. Запишите словосочетание «прямоугольный параллелепипед». 2. Сколько граней имеет прямоугольный параллелепипед? 3. Сколько рёбер имеет прямоугольный параллелепипед? 4. Сколько вершин имеет прямоугольный параллелепипед? 5. Какой фигурой является каждая грань прямоугольного параллелепипеда? 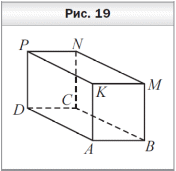 6. Как называют измерения прямоугольного параллелепипеда? 6. Как называют измерения прямоугольного параллелепипеда? 7. Закончите предложение. Куб — это прямоугольный параллелепипед, у которого …. 8. Какой фигурой является каждая грань куба? 9. На рисунке 19 изображён прямоугольный параллелепипед ABCDKMNP. Укажите: 1) нижнюю грань; 2) боковые рёбра; 3) рёбра, которые равны ребру AB; 4 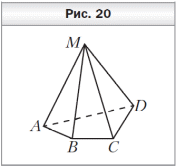 ) вершины, принадлежащие задней грани; ) вершины, принадлежащие задней грани; 5) грань, которая равна грани BMNC; 6) грани, которым принадлежит вершина C; 7) грани, для которых ребро AD является общим. 10. На рисунке 20 изображена пирамида MABCD. Укажите: 1) вершину пирамиды; 2) основание пирамиды; 3) боковые рёбра пирамиды; 4) боковые грани, для которых ребро MC является общим; 5) вершины основания, не принадлежащие боковой грани AMB. 11. Чему равно ребро куба, который можно сложить из 64 кубиков, рёбра которых равны 1 см? 12. Сколько необходимо проволоки для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 2 см, 4 см и 5 см? 13. Сколько квадратных сантиметров бумаги требуется, чтобы обклеить одним слоем прямоугольный параллелепипед, измерения которого равны 10 см, 20 см и 30 см? Диктант 20 по теме «Объём прямоугольного параллелепипеда» 1. Закончите предложение. 1) Измерить объём фигуры — значит подсчитать, сколько в ней помещается …. 2) Объём куба с ребром 1 см называют …. 3) Кубическим дециметром называют …. 4) Объём прямоугольного параллелепипеда равен …. 5) Объём куба, ребро которого равно a, вычисляют по формуле …. 2. Чему равен объём тела, составленного из 7 равных кубов, если ребро каждого куба имеет длину 3 см? 3. Объём сосуда равен 6 дм3. Поместятся ли в этом сосуде 7 л воды? 4. Сколько кубических сантиметров содержится: 1) в одном кубическом дециметре; 2) в одном кубическом метре? 5. Чему равен объём прямоугольного параллелепипеда с измерениями 2 см, 5 см и 12 см? 6. Запишите в кубических сантиметрах 2 дм3 4 см3. 7. Найдите объём прямоугольного параллелепипеда, измерения которого равны 15 см, 1 дм и 4 см. 8. Ребро куба, изготовленного из алюминия, равно 5 см. Найдите массу этого куба, если масса 1 см3 алюминия равна 3 г. 9. Во сколько раз объём куба, ребро которого 4 см, больше объёма куба, ребро которого 2 см? Диктант 21 по теме «Понятие обыкновенной дроби» 1. Запишите дроби:  . Подчеркните дроби, числитель которых равен 15. . Подчеркните дроби, числитель которых равен 15. 2. Запишите словами, как читается число  . . 3. Как называется: 1) шестидесятая часть часа; 2) десятая часть метра; 3) тысячная часть килограмма? 4. Приведите пример дроби: 1) знаменатель которой на 4 больше её числителя; 2) числитель которой на 6 меньше её знаменателя. 5. Петя покрасил забор за 5 ч. Какую часть забора он покрасил за 3 ч? 6. Оля купила 10 кг яблок и груш. Яблок было 4 кг. Какую часть купленных фруктов составляют: 1) яблоки; 2) груши? 7. Площадь прямоугольника равна 24 см2. Сколько квадратных сантиметров составляют  его площади? его площади? 8. Марина испекла пирожки, из которых 15 было с вишнями, что составляет  всех пирожков. Сколько всего пирожков испекла Марина? всех пирожков. Сколько всего пирожков испекла Марина?Диктант 22 по теме «Правильные и неправильные дроби. Сравнение дробей» 1. Закончите предложение. 1) Если числитель дроби равен знаменателю, то дробь равна …. 2) Правильной называют дробь, у которой …. 3) Неправильной называют дробь, у которой …. 4) Из двух дробей с одинаковыми знаменателями больше та, у которой …. 5) Из двух дробей с одинаковыми числителями больше та, у которой …. 6) На координатном луче из двух дробей большая дробь расположена …. 2. Запишите все неправильные дроби с числителем 5. 3. Запишите все натуральные значения x, при которых дробь  будет правильной. будет правильной. 4. Запишите дроби:  . Подчеркните правильные дроби. . Подчеркните правильные дроби.5. Запишите дроби:  . Подчеркните дроби, расположенные на координатном луче правее числа 1. . Подчеркните дроби, расположенные на координатном луче правее числа 1. 6. Сравните числа: 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  . .7. Правильной или неправильной является дробь  , если: , если: 1) y = 10; 2) y = 14; 3) y = 1; 4) y = 11? 8. Запишите в порядке возрастания четыре первые неправильные дроби: 1) со знаменателем 8; 2) с числителем 8. 9. Запишите все натуральные значения x, при которых выполняется неравенство: 1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4)  . .Диктант 23 по теме «Сложение и вычитание дробей с одинаковыми знаменателями» 1. Закончите предложение. 1) В буквенном виде правило сложения дробей с одинаковыми знаменателями записывают так: …. 2) В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так: …. 3) Сумма чисел  и и  равна …. равна ….4) Разность чисел  и и  равна …. равна ….5) Суммой чисел  и 0 является число …. и 0 является число …. 6) Дробь  является суммой чисел является суммой чисел  и …. и …. 7) Дробь  в виде суммы трёх разных дробей со знаменателем 7 можно представить так: …. в виде суммы трёх разных дробей со знаменателем 7 можно представить так: …. 2. Чему равно значение выражения: 1)  ? ? 3. Запишите корень уравнения: 1)  . .Диктант 24 по теме «Дроби и деление натуральных чисел. Смешанные числа» 1. Закончите предложение. 1) Черту дроби можно рассматривать как знак арифметического действия …. 2) Результат деления двух натуральных чисел может быть …. 3) Любое натуральное число можно записать в виде дроби …. 4) В смешанном числе 5  число 5 называют …. число 5 называют ….5) В смешанном числе 5  дробь дробь  называют…. называют…. 2. Запишите частное чисел 21 и 7 в виде дроби. 3. Запишите дробь  в виде частного. в виде частного. 4. Запишите число 15 в виде дроби со знаменателем 3. 5. Какому натуральному числу равна дробь  ? ?6. Целая часть числа равна 7, а дробная —  . Запишите это число в виде смешанного числа. . Запишите это число в виде смешанного числа. 7. Выделите из числа  целую и дробную части. целую и дробную части. 8. Запишите все неправильные дроби со знаменателем 6, у которых можно выделить целую часть, равную 3. 9. Запишите в виде неправильной дроби число 5  . . 10. При каком значении x выполняется равенство: 1)  11. Чему равно значение выражения: 1)  ; 2) 1 ; 2) 1 ; 3) 4 ; 3) 4 ; 4) ; 4)  ? ?12. Доску, длина которой равна  м, разрезали на равные части длиной м, разрезали на равные части длиной  м. На сколько частей разрезали доску? м. На сколько частей разрезали доску?Диктант 25 по теме «Представление о десятичной дроби» 1. Запишите десятичную дробь: 1) 4,6; 2) 1,02; 3) 4,008; 4) 52,19; 5) 0,09. 2. Запишите, как читается число 106,0504. 3. Запишите неправильную дробь 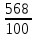 в виде десятичной дроби. в виде десятичной дроби. 4. Запишите десятичную дробь 6,072. Сколько единиц в разряде десятых этой дроби? 5. Запишите в виде десятичной дроби число, в котором семь единиц, одна сотая, шесть тысячных. 6. Выразите 8 см 2 мм в сантиметрах и запишите в виде десятичной дроби. 7. Выразите 48 кг в тоннах и запишите в виде десятичной дроби. 8. Запишите в виде десятичной дроби частное 3 576 : 100. Диктант 26 по теме «Сравнение десятичных дробей» 1. Запишите дробь 0,14 и равную ей десятичную дробь с тремя цифрами после запятой. 2. Сравните числа: 1) 4,783 и 5,1; 3) 0,18 и 0,2; 5) 32,004 и 31,005; 2) 3,25 и 3,198; 4) 0,6 и 0,495; 6) 2,305 и 2,3050. 3. Запишите все значения x, которые являются десятичными дробями с одной цифрой после запятой и при которых верно неравенство 3,41 < x < 3,95. 4. Укажите наибольшее натуральное значение x, при котором выполняется неравенство: 1) 3x < 28,2; 2) 5x < 40,6; 3) x + 6 < 12,5. 5. Укажите наименьшее натуральное значение x, при котором выполняется неравенство: 1) x + 5 > 7,24; 2) x − 12 > 9,863; 3) 7x > 58,9. 6. Запишите наибольшую десятичную дробь, у которой две цифры после запятой и которая меньше 60. 7. Запишите наименьшую десятичную дробь, у которой три цифры после запятой и которая больше 15. Диктант 27 по теме «Округление чисел» 1. Округлите до единиц число 7,36. 2. Округлите до десятых число 2,48. 3. Округлите до сотых число 1,295. 4. Округлите до десятков число 431,8. 5. Округлите до сотен число 2161. 6. Запишите 5382 кг в тоннах, предварительно округлив до тысяч. 7. Запишите 274 см в метрах, предварительно округлив до сотен. 8. Запишите все цифры, которые можно поставить вместо звёздочки, чтобы округление 4,38*3 ≈ 4,38 было выполнено верно. Диктант 28 по теме «Сложение и вычитание десятичных дробей» 1. Вычислите: 1) 0,3 + 0,4; 4) 1,3 + 0,5; 7) 4,1 + 2,59; 10) 3 − 0,2; 2) 0,8 + 0,6; 5) 8 + 0,7; 8) 3,2 − 1,8; 11) 1 − 0,1; 3) 0,6 + 0,4; 6) 1,23 + 5,46; 9) 5,4 − 0,6; 12) 10 − 9,5. 2. Найдите сумму: 1) 0,4 + 3; 2) 0,04 + 0,3; 3) 4 + 0,03; 4) 0,04 + 0,003. 3. Найдите разность: 1) 40 − 0,3; 2) 400 − 0,3; 3) 4 − 0,03; 4) 0,4 − 0,03. 4. Запишите натуральное число, расположенное на координатном луче ближе всего к числу 2,8. На сколько это число отличается от данного? 5. Запишите натуральное число, расположенное на координатном луче ближе всего к числу 3,4. На сколько это число отличается от данного? 6. Решите уравнение: 1) x + 0,16 = 0,5; 2) 8 − x = 2,6; 3) x − 4,23 = 4,7. Диктант 29 по теме «Умножение десятичных дробей» 1. Закончите предложение. 1) Если в одном числе три цифры после запятой, а во втором — две цифры, то в произведении этих чисел запятой надо отделить …. 2) При умножении десятичной дроби на 1 000 запятую надо перенести …. 3) При умножении десятичной дроби на 0,01 запятую надо перенести …. 2. Выполните умножение: 1) 5 ⋅ 0,3; 4) 3,5 ⋅ 0,2; 7) 0,13 ⋅ 4; 10) 5 ⋅ 0,14; 2) 0,2 ⋅ 0,6; 5) 0,3 ⋅ 8; 8) 0,9 ⋅ 0,7; 11) 40 ⋅ 0,5; 3) 0,4 ⋅ 7; 6) 1,4 ⋅ 2; 9) 1,1 ⋅ 0,6; 12) 0,12 ⋅ 0,4. 3. Умножьте на 10 число: 1) 0,3; 3) 4,06; 5) 0,001; 2) 2,4; 4) 0,406; 6) 1,005. 4. Умножьте на 1 000 число: 1) 0,024; 2) 0,005; 3) 0,38; 4) 0,7; 5) 2,3. 5. Автомобиль движется со скоростью 60 км/ч. Сколько километров он проедет за 0,8 ч? Диктант 30 по теме «Деление десятичных дробей» 1. Выполните деление: 1) 4,8 : 2; 3) 4,8 : 12; 5) 1,2 : 4; 7) 10 : 4; 2) 4,8 : 6; 4) 4,8 : 10; 6) 3 : 2; 8) 0,09 : 9. 2. За 4 ч турист прошёл 10,8 км. С какой скоростью двигался турист? 3. Найдите частное: 1) 8,4 : 0,2; 3) 1,2 : 0,06; 5) 8 : 0,2; 7) 20 : 0,02; 2) 0,08 : 0,4; 4) 0,36 : 0,4; 6) 0,6 : 0,3; 8) 4,5 : 0,09. 4. Выполните деление: 1) 14,8 : 10; 2) 3,67 : 10; 3) 0,4 : 100; 4) 345 : 1 000. 5. Выполните деление: 1) 14,8 : 0,1; 2) 3,67 : 0,1; 3) 0,4 : 0,01; 4) 345 : 0,001. 6. Чему равна ширина прямоугольника, площадь которого равна 9 см2, а длина — 6 см? 7. Какой десятичной дроби равна дробь: 1)  ; 2) ; 2) 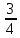 ; 3) ; 3) 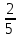 ; 4) ; 4) 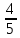 ; 5) ; 5) 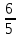 ; 6) ; 6) 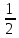 ? ? Диктант 31 по теме «Среднее арифметическое. Среднее значение величины» 1. Найдите среднее арифметическое чисел: 1) 8,1 и 8,3; 2) 1,2; 1,3 и 1,4; 3) 0,4; 0,6; 0,7 и 1,5. 2. Турист шёл 2 ч со скоростью 5 км/ч и 3 ч со скоростью 4 км/ч. Какова средняя скорость движения туриста? 3. Сумма шести чисел равна 45. Чему равно их среднее арифметическое? 4. Среднее арифметическое трёх чисел равно 7,1. Чему равна сумма этих чисел? 5. Среднее арифметическое двух чисел равно 9. Одно из этих чисел равно 6,5. Найдите второе число. Диктант 32 по теме «Проценты» 1. Закончите предложение. 1) Процентом называют …. 2) 1 % рубля — это …. 3) 1 % дециметра — это …. 4) 10 % минуты, выраженные в секундах, равны …. 2. Сколько сантиметров составляют 19 % метра? 3. Сколько килограммов составляют 23 % тонны? 4. Сколько минут составляют 10 % часа? 5. Сколько процентов числа составляет его: 1) половина; 3) пятая часть; 2) четверть; 4) три четверти? 6. В кинотеатре 500 мест. Во время сеанса было занято 90 % всех мест. Сколько зрителей смотрело фильм? 7. Свёкла содержит 22 % сахара. Сколько сахара получат, если переработают 600 т свёклы? 8. Раствор содержит соль и воду. Соль составляет 12 % раствора. Сколько процентов составляет вода? 9. Сплав состоит из меди, цинка и алюминия. Медь составляет 58 % сплав а, цинк — 34 %. Сколько процентов сплава составляет алюминий? 10. Запишите число 0,48 в виде процентов. 11. Если 7 % пути составляют 28 км, то сколько километров составляет весь путь? 12. Бронза — это сплав, 90 % которого составляет медь. Сколько получили килограммов бронзы, если для её изготовления взяли 27 г меди? |
