Курсовая работа (статика) 2 семестр. Курсовая работа (статика). Курсовая работа по статике расчет плоских и пространственных конструций
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
Часть 2. Расчёт плоских составных конструкций 2.1 Схема 1 Дано: F= 14 кН, P= 12 кН, q= 3 кН/м, qmax= 6 кН/м, М= 15 кНм, а= 0,9м,b = 1,2 м,r= 0,2м, R= 0,4м, α=300, β=1200 Определить: RА ,МА, RВ, RC  Рис.2.1 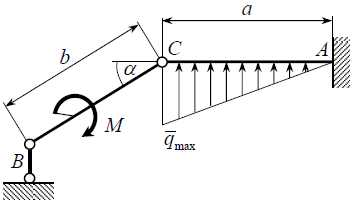 Решение: Разделим конструкцию на две части: горизонтальную балку AС и наклонную балку BC, освободив ее от внешних связей – жесткой заделки А и стержневой опоры В и от внутренней связи – шарнира С. Расчетные схемы изображены на рис. 2.2, на котором использованы следующие обозначения: 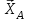 , , 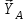 - составляющие реакции в жесткой заделке А - составляющие реакции в жесткой заделке АМА - реактивный момент в жесткой заделке А 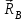 - реакция стержневой опоры В - реакция стержневой опоры В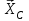 , , 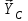 – составляющие реакции шарнира С на балку AС; – составляющие реакции шарнира С на балку AС;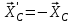 , , 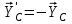 – составляющие реакции шарнира С на балку BС; – составляющие реакции шарнира С на балку BС;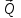 - равнодействующая распределенной нагрузки. - равнодействующая распределенной нагрузки.Равнодействующая распределенной нагрузки 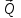 приложена на расстоянии приложена на расстоянии 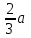 от жесткой заделки А, а ее модуль определяется по формуле от жесткой заделки А, а ее модуль определяется по формуле 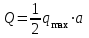 . . Рис. 2.2 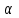 Рассмотрим равновесие балки ВС (рис. 2.2, б): Уравнение проекций сил на ось Х: 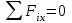 , , 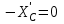 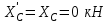 Уравнение моментов сил относительно точки С: 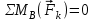 , , 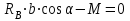 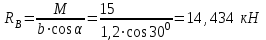 Уравнение проекций сил на ось Y: 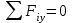 , , 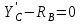 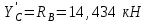 Для балки АС составим уравнение моментов сил относительно точки А: 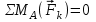 , , 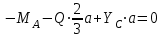 Откуда получаем: 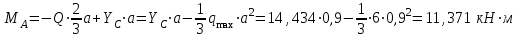 Уравнения проекций сил на оси координат: 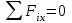 , , 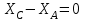 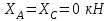 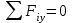 , , 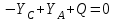 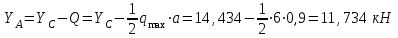 Ответ: 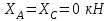 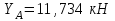 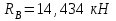 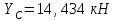 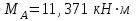 2.2 Схема 2 Дано: F= 14 кН, P= 12 кН, q= 3 кН/м, qmax= 6 кН/м, М= 15 кНм, а= 0,9м,b = 1,2 м,r= 0,2м, R= 0,4м, α=300, β=1200 Определить: RА ,МА, RВ, RC  Рис.2.3 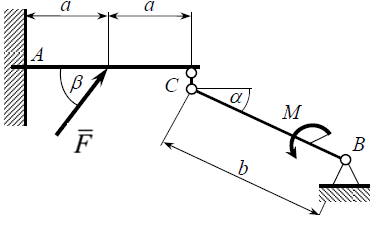 Решение: Расчленим конструкцию на две части: горизонтальную балку AС и наклонную балку BC, освободив ее от внешних связей – жесткой заделки А и неподвижного шарнира В и от внутренней связи – подвижной шарнирной опоры С. Расчетные схемы изображены на рис. 2.4, на котором использованы следующие обозначения: 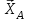 , , 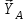 - составляющие реакции в жесткой заделке А - составляющие реакции в жесткой заделке АМА - реактивный момент в жесткой заделке А 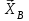 , , 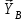 - составляющие реакции в шарнире В - составляющие реакции в шарнире В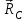 - реакция подвижной шарнирной опоры на балку ВС - реакция подвижной шарнирной опоры на балку ВС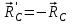 – реакция подвижной шарнирной опоры на балку АС; – реакция подвижной шарнирной опоры на балку АС; Рис. 2.4 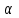 Составим уравнения равновесия балки ВС (рис. 2.4, б): 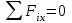 , , 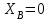 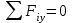 , , 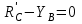 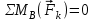 , , 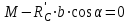 Откуда получаем: 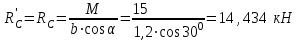 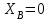 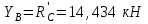 Уравнения равновесия балки АС (рис. 2.4, а): 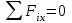 , , 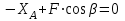 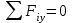 , , 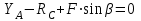 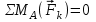 , , 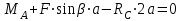 Откуда находим: 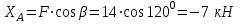 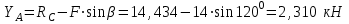 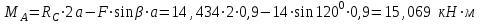 Ответ: 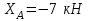 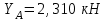 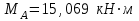 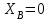 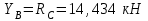 2.3 Схема 3 Дано: F= 14 кН, P= 12 кН, q= 3 кН/м, qmax= 6 кН/м, М= 15 кНм, а= 0,9м,b = 1,2 м,r= 0,2м, R= 0,4м, α=300, β=1200 Определить: ХА ,RВ  Рис. 2.5 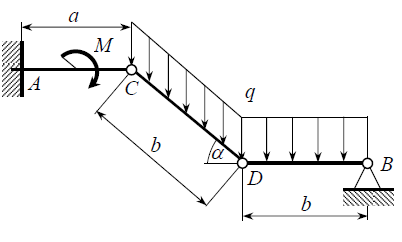 Решение: Для определения реакции YВ рассмотрим равновесие балки BD (рис.2.6,а); реакции ХВ - равновесие балки BD и CD (рис.2.6,б); реакции ХА - равновесие всей конструкции (рис.2.6,в); освободив их от внешних связей – жесткой заделки А и неподвижного шарнира В и от внутренних связей – шарниров С и D. Расчетные схемы изображены на рис. 2.6, на котором использованы следующие обозначения: 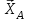 , , 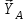 - составляющие реакции в жесткой заделке А - составляющие реакции в жесткой заделке АМА - реактивный момент в жесткой заделке А 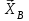 , , 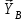 - составляющие реакции в шарнире В - составляющие реакции в шарнире В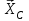 , , 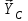 – составляющие реакции шарнира С на балку AС; – составляющие реакции шарнира С на балку AС;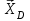 , , 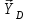 – составляющие реакции шарнира D на балку BD; – составляющие реакции шарнира D на балку BD;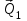 - равнодействующая распределенной нагрузки на участке CD, модуль которой - равнодействующая распределенной нагрузки на участке CD, модуль которой 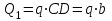 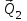 - равнодействующая распределенной нагрузки на участке AC, модуль которой - равнодействующая распределенной нагрузки на участке AC, модуль которой 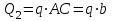  Рис. 2.6 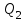 Составим уравнение моментов сил относительно точки D для балки ВD (рис. 2.6, a): 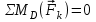 , , 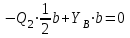 Откуда получим: 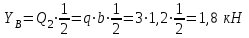 Составим уравнение моментов сил относительно точки С для системы, состоящей из балок ВD и CD (рис. 2.6, б): 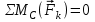 , , 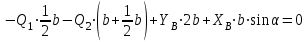 Откуда получим: 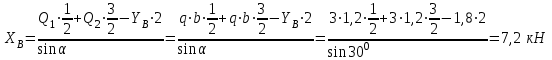 Уравнение проекций сил для всей конструкции (рис. 2.6, в): 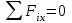 , , 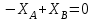 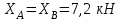 Ответ: 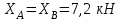 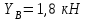 2.4 Схема 4 Дано: F= 14 кН, P= 12 кН, q= 3 кН/м, qmax= 6 кН/м, М= 15 кНм, а= 0,9м,b = 1,2 м,r= 0,2м, R= 0,4м, α=300, β=1200 Определить: ХА ,ХC  Рис. 2.7 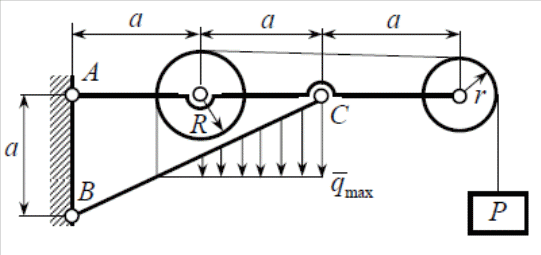 Решение: Для нахождения реакции ХА рассмотрим равновесие всей конструкции. Расчетная схема изображена на рис.2.8,а. На ней использованы следующие обозначения : 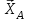 , , 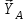 - составляющие реакции в шарнире А - составляющие реакции в шарнире А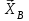 , , 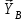 - составляющие реакции в шарнире В - составляющие реакции в шарнире В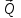 - равнодействующая распределенной нагрузки. - равнодействующая распределенной нагрузки.Равнодействующая распределенной нагрузки 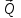 приложена на расстоянии приложена на расстоянии 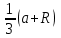 от шарнира С, а ее модуль определяется по формуле от шарнира С, а ее модуль определяется по формуле 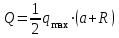 . .Составим уравнение моментов сил относительно точки В для всей конструкции: 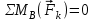 , , 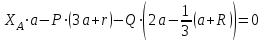 Или 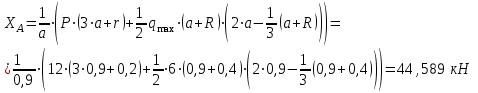  Рис. 2.8 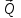 Для нахождения реакции ХС рассмотрим равновесие балки AC с блоками и грузом P. Расчетная схема изображена на рис.2.8,б. На ней использованы следующие обозначения : 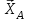 , , 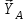 - составляющие реакции в шарнире А - составляющие реакции в шарнире А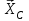 , , 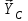 – составляющие реакции шарнира С на балку BС; – составляющие реакции шарнира С на балку BС;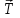 –реакция нити на балку ВС; –реакция нити на балку ВС;Так как нить невесомая, а трением на блоках пренебрегаем, то T P. Составим уравнение проекций сил на ось Х: 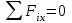 , , 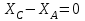 Откуда получаем: 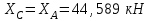 Ответ: 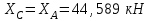 |
