Курсовая работа (статика) 2 семестр. Курсовая работа (статика). Курсовая работа по статике расчет плоских и пространственных конструций
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
Министерство образования и науки России ФГБОУ ВПО ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра теоретической механики Курсовая работа по статике «РАСЧЕТ ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ КОНСТРУЦИЙ» Вариант 06-3 Выполнил студент гр. ИБ360801 Коньков С.В. № зачетки 206236 Руководитель канд. техн. наук, доцент Ткач О.А. Тула, 2021 Оглавление Аннотация …………………………………………………………………… 3 Часть 1. Расчет плоской шарнирной фермы ………………………………. 4 Определение реакции опор аналитическим способом ………………… 4 Определение реакций опор графическим методом ……………………. 6 Определение усилий в стержнях фермы методом вырезания узлов ….. 8 Аналитический метод определения сил реакций стержней ………… 8 Графический метод определения сил реакций в стержнях фермы ... 12 Диаграмма Максвелла–Кремоны ………………………………………. 14 Метод Риттера …………………………………………………………… 16 Часть 2. Расчёт плоских составных конструкций ……………………….. 18 2.1 Схема 1 ………………………………………………………………. 18 2.2 Схема 2 ………………………………………………………………. 21 2.3 Схема 3 ………………………………………………………………. 24 2.4 Схема 4 ………………………………………………………………. 27 Часть 3. Расчет пространственной конструкции ………………………… 30 Выводы ……………………………………………………………………… 34 Список литературы ………………………………………………………… 35 Аннотация Исследуется равновесие твердых тел и их систем на примере таких технически важных конструкций, как плоские шарнирные фермы, балки, валы, плиты и пластинки с использованием аналитических и графических методов. Для каждой расчетной схемы составлены уравнения равновесия и определены реакции внешних и внутренних связей разными методами. Часть 1. Расчет плоской шарнирной фермы Схема Ф06 вариант 3 Дано: Р4=8кН; Р5=16кН;a=1м,b=2м,α=450  Рис. 1.1  Определение реакции опор аналитическим способом. Освободимся от связей, заменяя их действие силами реакций 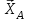 и и 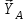 , , 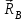 . . Таким образом, получили свободное тело, на которое действует система активных сил 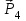 , , 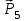 и сил реакций и сил реакций 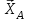 и и 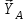 (направлены вдоль осей координат), (направлены вдоль осей координат), 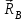 (направлена перпендикулярно поверхности, по которой может двигаться опора). (направлена перпендикулярно поверхности, по которой может двигаться опора).  Рис. 1.2 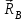 Составим уравнения равновесия для заданной фермы: 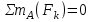 , , 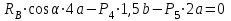 (1) (1)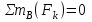 , , 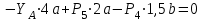 (2) (2)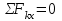 , , 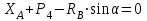 (3) (3)Решая эту систему уравнений получим: 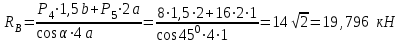 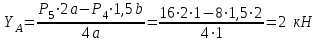 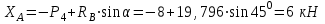 Для проверки полученных результатов составим уравнение проекций сил на ось Y: 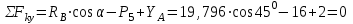 Следовательно, реакции найдены верно и окончательно получаем: 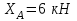 ; ; 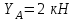 ; ; 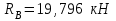 Определение реакций опор графическим методом Начинаем строить силовой многоугольник, составленный из сил, действующих на ферму, включая силы реакций. Так как силы реакций на данном этапе ещё неизвестны, то многоугольник оказывается недостроенным. Однако, линия действия одной из неизвестных сил 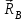 (направленной вдоль стержня) известна, и её можно указать на силовом многоугольнике так, как показано на рис. 1.3. (направленной вдоль стержня) известна, и её можно указать на силовом многоугольнике так, как показано на рис. 1.3. Рис. 1.3  Строим верёвочный многоугольник. Для этого на плане сил (масштаб 1см-2кН) выбираем произвольную точку О (полюс) и проводим лучи 1, 2, 3 в вершины силового многоугольника так, как показано на рис. 1.3. Направления полученных лучей переносим на основной чертеж, выполненный с учетом размеров (рис.1.4), следующим образом. Из точки А, в которой направление силы неизвестно, проводим прямую, параллельную лучу 1 до пересечения с линией действия ближайшей силы 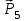 и получаем точку C (В нашем случае эта точка совпадает с точкой А). Из точки C проводим прямую, параллельную лучу 2 до пересечения с линией действия следующей силы и получаем точку C (В нашем случае эта точка совпадает с точкой А). Из точки C проводим прямую, параллельную лучу 2 до пересечения с линией действия следующей силы 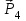 и получаем точку D. Из точки D проводим прямую, параллельную лучу 3 до пересечения с линией действия и получаем точку D. Из точки D проводим прямую, параллельную лучу 3 до пересечения с линией действия 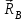 и получаем точку E. Полученный верёвочный многоугольник ACDE не замкнут. Замыкая его на точку А, получаем направление луча 4, который переносим на план сил и получаем точку пересечения с линией действия силы и получаем точку E. Полученный верёвочный многоугольник ACDE не замкнут. Замыкая его на точку А, получаем направление луча 4, который переносим на план сил и получаем точку пересечения с линией действия силы 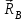 , а следовательно, величину и направление самой силы , а следовательно, величину и направление самой силы 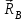 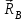  Рис. 1.4 В случае равновесия силовой многоугольник также должен быть замкнутым. Замыкая силовой многоугольник, вертикальной и горизонтальной линиями, получаем величину и направление составляющих реакции шарнира в точке А 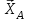 и и 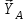 (рис. 1.3) (рис. 1.3)Находим значения искомых сил реакций, измеряя соответствующие вектора на плане сил с учётом выбранного масштаба: 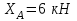 ; ; 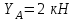 ; ; 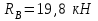 Полученные результаты совпадают с результатами, полученными аналитическим методом, в пределах погрешности измерений. Определение усилий в стержнях фермы методом вырезания узлов. Так как стержни являются невесомыми, то силы реакций будут направлены вдоль этих стержней. Стержни и узлы пронумеруем так, как показано на рис. 1.5. Определим силы реакций стержней фермы аналитически.  Рис. 1.5 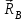 Аналитический метод определения сил реакций стержней. Для определения усилий в стержнях 1-13 вырежем узлы и рассмотрим равновесие сил, приложенных к каждому из них. Определим углы: 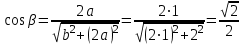 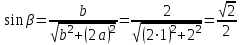 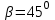 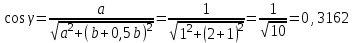 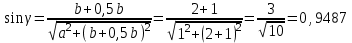 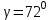  Рис. 1.6 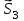 Узел I (рис.1.6,а): 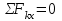 , , 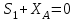 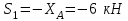 - стержень сжат - стержень сжат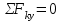 , , 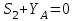 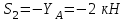 - стержень сжат - стержень сжатУзел II (рис.1.6,б): 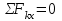 , , 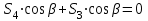 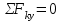 , , 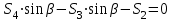 Из первого уравнения: 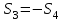 Тогда 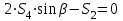 И 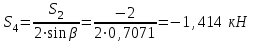 - стержень сжат - стержень сжат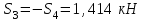 - стержень растянут - стержень растянут 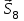  Рис. 1.7 Узел III (рис.1.7,а): 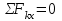 , , 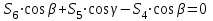 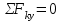 , , 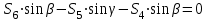 Из первого уравнения: 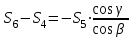 Тогда второе уравнение примет вид 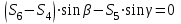 Или 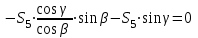 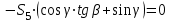 Так как 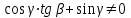 , то , то 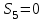 - стержень не нагружен - стержень не нагруженИ 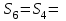 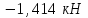 - стержень сжат - стержень сжат Узел IV (рис.1.7,б): 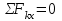 , , 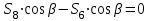 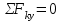 , , 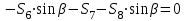 Откуда 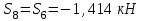 - стержень сжат - стержень сжат 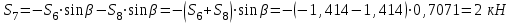 - стержень растянут - стержень растянут Рис. 1.8 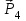 Узел V (рис.1.8,а): 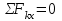 , , 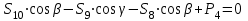 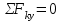 , , 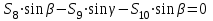 Из первого уравнения: 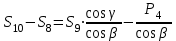 Тогда второе уравнение примет вид 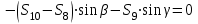 Или 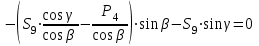 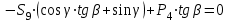 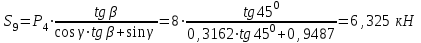 - стержень растянут - стержень растянутИ 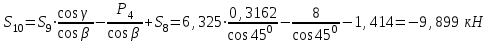 - стержень сжат - стержень сжат Узел VI (рис.1.8,б): 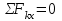 , , 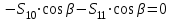 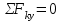 , , 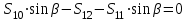 Откуда 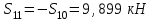 - стержень растянут - стержень растянут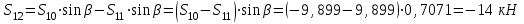 - стержень сжат - стержень сжат Рис. 1.9 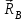 Узел VII: 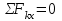 , , 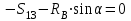 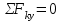 , , 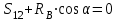 Из первого уравнения: 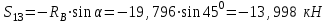 - стержень сжат - стержень сжатПодставив вычисленные ранее значения во второе уравнение, проверим правильность проведенных вычислений 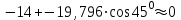 Расчеты проведены верно. Сведем полученные данные в таблицу:
Графический метод определения сил реакций в стержнях фермы Силы реакций определяются из условия замкнутости силового многоугольника при равновесии для каждого из узлов фермы. вычертим в масштабе ферму и изобразим все приложенные к ней заданные силы и ранее определенные реакции опор; наметим последовательность узлов, которые необходимо вырезать для определения усилий в указанных стержнях (выбираем ту же последовательность обхода узлов, что и при аналитическом методе); вырезаем узел I, в котором сходятся два стержня, и рассмотреть его равновесие под действием заданных сил и реакций стержней; определим эти реакции построением в масштабе 1 см – 2 кН замкнутого многоугольника сил, приложенных к узлу; рассмотрим, переходя от узла к узлу, равновесие остальных узлов в намеченной последовательности: при этом в узле должно быть только две неизвестные реакции стержней; построив для каждого узла замкнутый силовой многоугольник, определим все искомые усилия в стержнях; Измерив полученные отрезки на плане сил с учётом выбранного масштаба, определим величины и направления неизвестных реакций, которые сведем в таблицу:
Полученные результаты совпадают с результатами, полученными аналитическим методом, в пределах погрешности измерений  Рис. 1.10 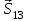 Диаграмма Максвелла–Кремоны Строим ферму в масштабе. Изображаем все силы, действующие на ферму. Обозначаем внешние поля — области чертежа, разделенные силами и стержнями фермы — А,В,С, D, E (рис. 1.11) Обозначаем внутренние поля F, G, H, I, J, K . Внешним нагрузкам и усилиям в стержнях даем новые имена — по соседним с силой (или стержнем) полям. Строим многоугольник внешних сил. Выберем направление обхода фермы по часовой стрелке. Начинаем с P4. Откладывая в масштабе (1cм-2кН) эту силу и соблюдая ее направление, обозначаем начальную и конечную точку строчными буквами a и b, соответствующими направлению обхода — из поля A в поле B. Следующая по часовой стрелке нагрузка — RB Строим ее в точке b вслед за силой P4. Конечную точку помечаем буквой c. Обход фермы продолжаем, пока многоугольник не замкнется. Последней будет сила реакция опоры XA, обозначенная как EA. Конец ее попадает на исходную точку. Строим точки внутренних полей на диаграмме. Точку, соответствующую внутреннему полю, можно найти, если у этого поля построены два соседних с ним поля. Таким образом, начинать графический расчет можно с поля F, у которого соседние поля А и D определены на диаграмме. По направлению стержней AF и FD проводим линии через точки a и b диаграммы. Точка их пересечения - f. Длины аf и bf равны значениям усилий в соответствующих стержнях. Аналогично находим усилия в остальных стержнях. При получении последней точки автоматически выполняется проверка. Точка k строилась на пересечении линий kj и ck, то проверкой является прямая kb. Она параллельна соответствующему стержню KB, значит, диаграмма построена верно. Окончательные результаты заносим в таблицу:
Полученные результаты совпадают с результатами, полученными аналитическим методом, в пределах погрешности измерений и масштаба построения диаграммы  Рис. 1.11 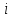 Метод Риттера Определим усилия в стержнях 1,3,4. Для определения нужного усилия по методу Риттера рассечем ферму по этим стержням на части и рассмотрим равновесие левой части (рис.1.12). Действие отброшенной части заменим действием сил реакций.  Рис. 1.12 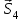 Составим уравнения равновесия для полученной части фермы: Уравнение моментов относительно узла II: 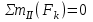 , , 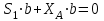 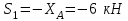 Уравнение моментов относительно узла VIII: 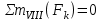 , , 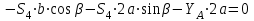 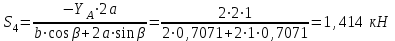 Уравнение проекций сил на ось X: 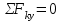 , , 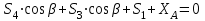 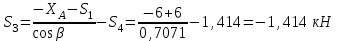 Полученные результаты совпадают с предыдущими расчетами |
