Курсовая работа Решение систем линейных уравнений по методу Гаусса

• Название: Курсовая работа Решение систем линейных уравнений по методу Гаусса
• Дата: 18.09.2022
• Размер: 102.12 Kb.
• Имя файла: Kudryavtseva_L_A_S21-RES.docx
• Тип: Курсовая; #683810

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. Р. Е. АЛЕКСЕЕВА

ИНСТИТУТ РАДИОЭЛЕКТРОНИКИ И ИНФОРМАЦИОННЫХ

ТЕХНОЛОГИЙ

КУРСОВАЯ РАБОТА

«Решение систем линейных уравнений по методу Гаусса»

Выполнил:

студент группы С21-РЭС

Кудрявцева Л.А.

Проверил:

доцент кафедры ИРС

С. Б. Сидоров

Нижний Новгород

2022

СОДЕРЖАНИЕ

1. Введение 2

2. Постановка задачи 3

3. Руководство пользователя 4

4. Руководство программиста 7

4.1. Структура программы 7

4.2. Структуры данных 8

4.3. Алгоритм решения СЛАУ методом Гаусса 8

4.4. Алгоритм ввода/вывода матрицы 8

4.5. Основные функции в программе 8

5. Заключение 9

6. Список рекомендованной литературы 10

7. Приложение 11

7.1. Главный модуль программы 11

7.2. Модуль «Основной модуль» 11

7.3. Модуль «Хранилище Информации» 13

7.4. Модуль «Пользовательский интерфейс» 13

7.5. Модуль «Метод Гаусса» 17

1. Введение

В данной работе рассматривается решение задачи разработки программной системы для решения систем линейных алгебраических уравнений (СЛАУ) по методу Гаусса. Метод Гаусса - классический метод решения СЛАУ, состоящий в постепенном понижении порядка системы и исключении неизвестных.

Одним из способов преодоления сложности данной задачи является использование технологии разработки программ «сверху-вниз». Данный метод проектирования позволяет путем декомпозиции исходной задачи свести её к последовательному решению более простых задач. Его использование позволяет уменьшить затраты на отладку и повысить надёжность программы. Также существенным моментом технологии «сверху-вниз» является её акцент на повторное использование уже существующих модулей, а не на разработку их «с нуля».

В начале основной части отчёта приводится постановка задачи с указанием полного набора операций, выполнение которых должна обеспечивать данная программа.

В руководстве пользователя раскрывается назначение программы, её возможности и выполняемые операции. Здесь подробно объясняются правила пользования программой и приводятся конкретные примеры диалога с пользователем.

В руководстве программиста рассматриваются вопросы внутренней организации программы, в том числе ее состав модулей и их взаимодействие.

В заключении делаются выводы о полноте решения поставленной задачи, а также приводится ряд соображений по возможным направлениям доработки полученной прикладной программы.

Также приведена техническая информация, включающая листинги всех модулей программы.

2. Постановка задачи

Требуется разработать приложение, которое позволяет пользователю решить систему линейных алгебраических уравнений по методу Гаусса.

Размерность системы уравнений n, коэффициенты матрицы a и вектор 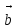задаются пользователем. Также необходимо учесть возможность как несовместной системы, так и наличия бесконечного числа решений.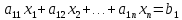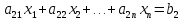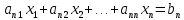





. . . . . . . . . .



Таким образом, программа должна посчитать значения 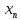, которые будут являться решениями СЛАУ, а также наглядно продемонстрировать процесс решения системы уравнений на экране монитора.

Кроме этого, программная система должна обеспечивать возможность проведения серийных экспериментов, когда вычисления осуществляются несколько раз с различными исходными данными.

Программные модули, содержащие подпрограммы решения задач, не должны привязываться к конкретным значения параметров, в данном случае к количеству уравнений СЛАУ.

3. Руководство пользователя

Данная программная система предназначена для решения систем линейных алгебраических уравнений по методу Гаусса. Она позволяет решать СЛАУ с различным числом уравнений.

Запуск программы осуществляется либо набором в командной строке имени программы с последующим нажатием на клавишу «Enter», либо каким-то другим способом, зависящим от конкретной операционной системы.

После запуска программы на экране монитора появляется краткое информационное сообщение, где будет указана основная информация о программе.



Рис 1

Программа является интерактивным консольным приложением. Весь диалог с пользователем осуществляется в текстовом режиме через систему меню. Меню появляется автоматически после выдачи информационного сообщения и имеет следующую структуру:



Рис 2

После отображения меню пользователю предлагается указать кол-во СЛАУ или 0 для выхода

После ввода кол-ва СЛАУ запрашивается информация о каждой из них последовательно: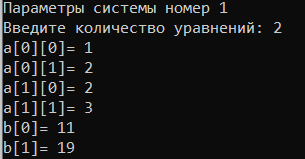



Рис 3

Далее, если все данные введены корректно, программа выводит на экран введённую вами систему (или несколько), процесс ее решения и ответ: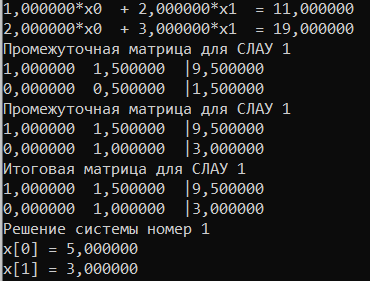



Рис 4

Далее программа выводит на экран процесс решения и ответ нескольких СЛАУ (количество зависит от указанных параметров).

Примечания

В программе предусмотрена возможность как несовместности системы, так и наличия бесконечного числа решений. В данных случаях программа выводит на экран соответствующее сообщение:



Рис 5

4. Руководство программиста

4.1. Структура программы

В основе данной программы лежат принципы модульного программирования. Она является совокупностью взаимодействующих модулей. Структура программы представлена на рисунке.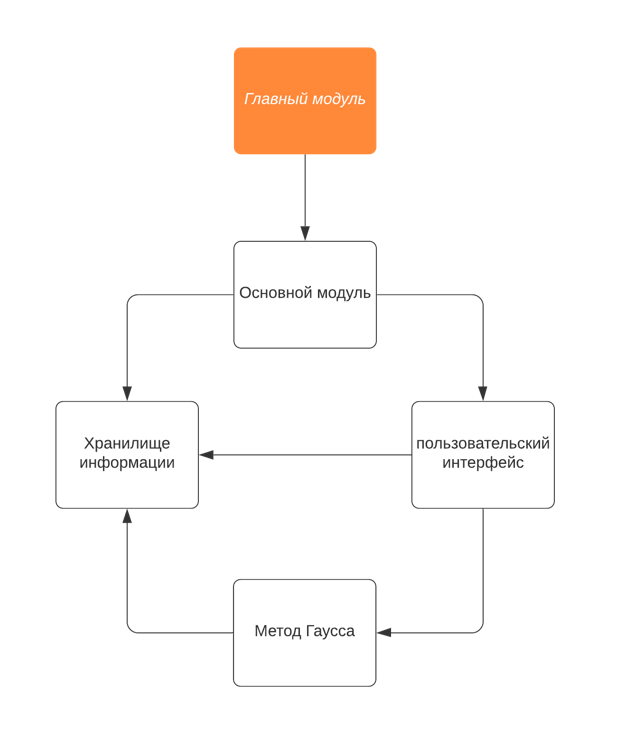



Рис 6

Программа состоит из 7 модулей, назначение каждого из которых приведено ниже:

1. main.cpp – главный модуль программы;

2. baseModule.c, baseModule.h – исполнитель «Основной модуль». Управляет программой в целом, вызывает необходимые функции;

3. informationHolder.h – исполнитель «Хранилище Информации». Предназначен для правильной организации хранения информации во время работы.;

4. userInterface.c, userInterface.h– исполнитель «Пользовательский интерфейс».Предназначен для запроса и передачи информации от пользователя и организации ввода-вывода информации;

5. gauss.h, gauss.c – исполнитель «Метод Гаусса». Предназначен для решения СЛАУ и вывода решений на экран монитора.

4.2. Структуры данных

Введенные пользователем коэффициенты матриц a и вектор 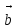хранятся в динамическом массиве структур (по одной структуре для описания свойств каждой СЛАУ), сами структуры состоят из одного двумерного динамического массива для хранения коэффициентов А, по одному одномерному массиву для ответов на ур-я (вектор b), а так же дополнительных полей для хранения решения, индикации совместности/несовместности системы а так же кол-ва уравнений а соответственно и кол-ва неизвестных.

4.3. Алгоритм решения СЛАУ методом Гаусса

Алгоритм решения СЛАУ заключается в постепенном приведении матрицы к ступенчатому виду. Сначала находим наибольший по модулю элемент в матрице. Проверяем на данном этапе имеет ли система решение или множество решений. Когда нашли максимальный элемент переставляем столбцы и строки так что бы поменять местами текущий и максимальный элемент. Меняем индексы также, как и столбцы. После этого идет алгоритм прямого хода метода гаусса, систему приводим к ступенчатой или треугольной форме. Следующий алгоритм находит неизвестные, все получившиеся результаты записывается в самый правый столбец. После чего они выводятся на экран монитора.

4.4. Алгоритм ввода/вывода матрицы

Алгоритм ввода и вывода коэффициентов системы линейных алгебраических состоит в организации вложенных циклов, с помощью которых происходит ввод и вывод элементов двумерного массива (коэффициентов системы уравнений) по отдельности.

for (int i = 0; i < currentSLAU->n; i++) // цикл последовательного заполнения коэф-в а

{

for (int j = 0; j < currentSLAU->n; j++)

{

printf("a[%d][%d]= ",i,j);

scanf("%lf",¤tSLAU->a[i][j]);

}

}

4.5. Основные функции в программе

void getInformationAboutCurrentSLAU(struct informationAboutSLAU *currentSLAU, int number) - функция осуществляет ввод информации о СЛАУ

void outputResults(struct informationAboutSLAU *currentSLAU,int number) - функция осуществляет вывод результата единичного или множественных вычислений.

intgauss (structinformationAboutSLAU *currentSLAU,intnumber) - функция решает СЛАУ методом Гаусса и записывает решение в структуру, возвращает определенный код при отсутствии решений.

5. Заключение

Для разработки программной системы для решения систем линейных алгебраических уравнений по методу Гаусса, в данной работе была использована технология проектирования «сверху-вниз». В результате проведенной отладки и испытаний с помощью контрольных примеров можно сделать вывод, что полученная программа решает поставленную задачу правильно и в полном объёме.

Диалог с пользователем в программе осуществляется в консольном режиме. Одним из возможных направлений доработки данной программы является реализация более наглядного графического интерфейса пользователя.

Кроме этого, перспективным направлением доработки данной программы является возможность загрузки коэффициентов СЛАУ из заданного пользовательского файла, а также сохранение решений в файл. Для этого потребуется переработать только модуль «Ввод», и создать дополнительный модуль «Сохранение в файл».

Так как все рассмотренные случаи доработки имеют локальный характер и не требуют изменений общей структуры программы, то можно сделать вывод о гибкости полученного программного обеспечения и, следовательно, об успешно проведенной декомпозиции задачи.

6. Список рекомендованной литературы

1. Брайан Керниган, Деннис Риччи, Язык программирования Си, 3-е издание.

2. Герберт Шилдт. Полный справочник по С (4-ое издание)

3. Орлов, С.А. Технологии разработки программного обеспечения. учеб. пособие. 2-е изд.

7. Приложение

7.1. Главный модуль программы

#include

#include "baseModule.h"

int main ()

{

return baseModule(); // запуск подпрограммы решения СЛАУ методом Гаусса

}

7.2. Модуль «Основной модуль»

baseModule.h

#ifndef baseModule_h

#define baseModule_h

#include

#include

#include "gauss.h"

#include "userInterface.h"

int baseModule(void); // Основной модуль

#endif /* baseModule_h */

baseModule.c

#include "baseModule.h"

int baseModule()

{

struct informationAboutSLAU *arrayOfSLAU = NULL; // инициализация массива из структур, каждая из которых хранит информацию об одном СЛАУ

while (1) // Бесконечный цикл до команды выхода из программы

{

clearScreen(); // очистка консоли (мультиплатформенная)

int quantityOfSlau = mainMenu(); // запрос кол-ва СЛАУ через главное меню

if (quantityOfSlau <= 0) // Выход из бесконечного цикла если было задано 0 СЛАУ

break;

if (quantityOfSlau == 1) // аллокация памяти в случае если только 1 СЛАУ

arrayOfSLAU = (struct informationAboutSLAU*)malloc(1*sizeof(struct informationAboutSLAU));

else

arrayOfSLAU = (struct informationAboutSLAU*)malloc(quantityOfSlau * sizeof(struct informationAboutSLAU)); // аллокация памяти если СЛАУ несколько

for (int i = 0; i < quantityOfSlau; i++) //цикл запросов информации о СЛАУ

{

getInformationAboutCurrentSLAU(&arrayOfSLAU[i],i); // функция ввода информации о СЛАУ

}

for (int i = 0; i < quantityOfSlau; i++) // цикл решения одной или нескольких СЛАУ одна за другой

{

gauss(&arrayOfSLAU[i],i); // функция решения Методом Гаусса, в нее передается указатель на конкретную (одну из массива) СЛАУ и номер этой СЛАУ

}

for (int i = 0; i < quantityOfSlau; i++) // цикл вывода решений

{

outputResults(&arrayOfSLAU[i],i); // функция вывода решения

}

free(arrayOfSLAU); // освобождение памяти

pauseConsole(); // "Заморозка" консоли для проверки результатов (мультиплатформенная)

}

return 0;

}

7.3. Модуль «Хранилище Информации»

#ifndef informationHolder_h

#define informationHolder_h

struct informationAboutSLAU //структура информации об одной слау

{

double **a,*b,*x; //заготовка под двумерный массив коэффициентов а, вектор b, массив решений x

int n; // количество ур-й в СЛАУ

int error; // переменная для индикации несовместности или не одного решения СЛАУ (1 если есть ошибка, 0 если одно решение)

};

#endif /* informationHolder_h */

7.4. Модуль «Пользовательский интерфейс»

userInterface.h

#ifndef userInterface_h

#define userInterface_h

#include

#include

#include "informationHolder.h"

void getInformationAboutCurrentSLAU(struct informationAboutSLAU *currentSLAU, int number); // функция ввода информации о СЛАУ

void outputSLAU(struct informationAboutSLAU *currentSLAU); // вывод СЛАУ в консоль в виде уравнений

void outputMatrix(struct informationAboutSLAU *currentSLAU, int mode, int number); // вывод СЛАУ в консоль в виде матрицы

void outputResults(struct informationAboutSLAU *currentSLAU,int number); //функция вывода решения

int mainMenu(void); // меню

void clearScreen(void); // очистка экрана

void pauseConsole(void);// "заморозка" консоли

#endif /* userInterface_h */

userInterface.c

#include "userInterface.h"

void getInformationAboutCurrentSLAU(struct informationAboutSLAU *currentSLAU, int number) // запрос информации о СЛАУ

{

printf("Параметры системы номер %d\n", number+1);

printf("Введите количество уравнений: ");

scanf("%d",¤tSLAU->n);

currentSLAU->a = (double**)malloc(currentSLAU->n * sizeof(double)); // аллокация памяти под двухмерный массив (из-за этого цикл)

for (int i = 0; i < currentSLAU->n; i++) {

currentSLAU->a[i] = (double*)malloc(currentSLAU->n * sizeof(double));

}

currentSLAU->b = (double*)malloc(currentSLAU->n * sizeof(double)); // аллокация памяти под ответы на каждое ур-е

for (int i = 0; i < currentSLAU->n; i++) // цикл последовательного заполнения коэф-в а

{

for (int j = 0; j < currentSLAU->n; j++)

{

printf("a[%d][%d]= ",i,j);

scanf("%lf",¤tSLAU->a[i][j]);

}

}

for (int i = 0; i < currentSLAU->n; i++) // цикл заполнения ответов на ур-я (вектора b)

{

printf("b[%d]= ",i);

scanf("%lf",¤tSLAU->b[i]);

}

outputSLAU(currentSLAU); // вывод СЛАУ в консоль в виде ур-й для проверки корректности ввода

}

void outputSLAU(struct informationAboutSLAU *currentSLAU){ // ф-я вывода СЛАУ в консоль в виде ур-й

for (int i = 0; i < currentSLAU->n; i++) // используется вложенный цикл т.к. это двухмерный массив

{

for (int j = 0; j < currentSLAU->n; j++)

{

printf("%lf*x%d ",currentSLAU->a[i][j],j);

if (j < currentSLAU->n - 1)

printf(" + ");

}

printf(" = %lf\n",currentSLAU->b[i]);

}

return;

}

void outputResults(struct informationAboutSLAU *currentSLAU,int number) // в-я вывода результатов работы программы (решений СЛАУ)

{

if (currentSLAU->error == 1) { // если индикатор ошибки = 1 то система несвм. или не имеет единственного решения

printf("Система %d несовместна или не имеет единственного решения \n",number+1);

return;

}

printf("Решение системы номер %d\n", number+1);

for (int i = 0; i < currentSLAU->n; i++)

printf("x[%d] = %lf\n",i,currentSLAU->x[i]);

}

int mainMenu(void) // меню ввода кол-ва СЛАУ

{

int temp = 0;

printf("Введите количество СИСТЕМ уравнений которое необходимо решить (1 если необходим один эксперимент, 2 или больше если необходимо произвести серию экспериментов) или 0 для выхода из программы.\n");

scanf("%d",&temp);

return temp;

}

void clearScreen() // ф-я очистки консоли использует условное компилирование для обеспечения работы на большинстве платформ

{

#if defined(__linux__) || defined(__unix__) || defined(__APPLE__)

system("clear");

#endif

#if defined(_WIN32) || defined(_WIN64)

system("cls");

#endif

printf("Решение СЛАУ методом Гаусса \n Гейман Владислав \n\n");

}

void pauseConsole() // ф-я остановки консоли использует условное компилирование для обеспечения работы на большинстве платформ

{

#if defined(_WIN32) || defined(_WIN64)

printf("Нажмите ENTER чтобы выйти в главное меню");

system("pause");

#endif

#if defined(__linux__) || defined(__unix__) || defined(__APPLE__)

system ("read -p \"Нажмите ENTER чтобы выйти в главное меню\" -n 1");

#endif

}

void outputMatrix(struct informationAboutSLAU *currentSLAU, int mode, int number) // ф-я вывода СЛАУ в консоль в виде матрицы

{

if (mode == 0)

printf("Промежуточная матрица для СЛАУ %d\n",number+1);

else

printf("Итоговая матрица для СЛАУ %d\n",number+1);

for (int i = 0; i < currentSLAU->n; i++)

{

for (int j = 0; j < currentSLAU->n; j++)

{

printf("%3lf",currentSLAU->a[i][j]);

if (j < currentSLAU->n - 1)

printf(" ");

}

printf(" |%3lf\n",currentSLAU->b[i]);

}

return;

}

7.5. Модуль «Метод Гаусса»

gauss.h

#ifndef gauss_h

#define gauss_h

#include

#include

#include "informationHolder.h"

#include "userInterface.h"

int gauss (struct informationAboutSLAU *currentSLAU,int number); // ф-я выполняющая вычисления по методу Гаусса

#endif /* gauss_h */

gauss.c

#include "gauss.h"

double module (double x) // небольшая ф-я берущая модуль (не использовал fabs чтобы не подключать тяжёлую библиотеку math.h

{

if (x < 0) {

x = -x;

}

return x;

}

int gauss (struct informationAboutSLAU *currentSLAU,int number)

{

double max;

int k, index;

const double eps = 0.00001; // точность решения

currentSLAU->x = (double*)malloc(currentSLAU->n);//аллокация памяти под ответы

k = 0;

while (k < currentSLAU->n) // попытка привести матрицу к "ступенчатому" или "треугольному" виду

{

// Поиск строки с максимальным a[i][k]

max = module(currentSLAU->a[k][k]);

index = k;

for (int i = k + 1; i < currentSLAU->n; i++)

{

if (module(currentSLAU->a[i][k]) > max)

{

max = module(currentSLAU->a[i][k]);

index = i;

}

}

// Перестановка строк

if (max < eps) // проверка на нулевые диагональные элементы

{

currentSLAU->error = 1;

return 0;

}

for (int j = 0; j < currentSLAU->n; j++) // пререстановка коэф-в

{

double temp = currentSLAU->a[k][j];

currentSLAU->a[k][j] = currentSLAU->a[index][j];

currentSLAU->a[index][j] = temp;

}

double temp = currentSLAU->b[k]; // перестановка ответов

currentSLAU->b[k] = currentSLAU->b[index];

currentSLAU->b[index] = temp;

// Нормализация уравнений

for (int i = k; i < currentSLAU->n; i++)

{

double temp = currentSLAU->a[i][k];

if (module(temp) < eps) continue; // для нулевого коэффициента пропустить

for (int j = 0; j < currentSLAU->n; j++)

currentSLAU->a[i][j] = currentSLAU->a[i][j] / temp;

currentSLAU->b[i] = currentSLAU->b[i] / temp;

if (i == k) continue; // уравнение не вычитать само из себя

for (int j = 0; j < currentSLAU->n; j++)

currentSLAU->a[i][j] = currentSLAU->a[i][j] - currentSLAU->a[k][j];

currentSLAU->b[i] = currentSLAU->b[i] - currentSLAU->b[k];

}

k++;

outputMatrix(currentSLAU,0,number); // вывод промежуточных матриц

}

outputMatrix(currentSLAU,1,number); // вывод финальной матрицы

// обратная подстановка

for (k = currentSLAU->n - 1; k >= 0; k--)

{

currentSLAU->x[k] = currentSLAU->b[k];

for (int i = 0; i < k; i++)

currentSLAU->b[i] = currentSLAU->b[i] - currentSLAU->a[i][k] * currentSLAU->b[k];

}

currentSLAU->error = 0;

return 1;

}