Теория телетрафика. Вариант 24. Курсовая работа студент IV курса факультета Визо группа зачетной книжки xxxx24 Вариант 24 задачи 1 и 4

• Название: Курсовая работа студент IV курса факультета Визо группа зачетной книжки xxxx24 Вариант 24 задачи 1 и 4
• Дата: 18.05.2019
• Размер: 117 Kb.
• Имя файла: Теория телетрафика. Вариант 24.doc
• Тип: Курсовая; #77668

Санкт-Петербургский

Государственный университет телекоммуникаций

им. проф. М.А. Бонч - Бруевича

ТЕОРИЯ ТЕЛЕТРАФИКА

Курсовая работа


Выполнил: студент IV курса

факультета ВиЗО

Группа

№ зачетной книжки xxxx24

Вариант 24

задачи 1 и 4

Вариант исходных данных №6

Санкт – Петербург

2011

Задача 1.
Исследование процесса поступления сообщений на системы коммутации

Условие: На телефонной станции организовано наблюдение за процессом поступления сообщений. Весь период наблюдения (25 ч), на протяжении которого поток является практически стационарным, разделен на n=100 интервалов длительностью t=15 мин. Для каждого интервала определяется число поступающих сообщений. Данные наблюдений группируются в статистический ряд по m членов, характеризующихся числом интервалов n_k (k = 1, 2, …, m) с одинаковым числом вызовов c_k в интервале.

№ п/п	ck	nk
1	0	5
2	1	15
3	2	22
4	3	23
5	4	17
6	5	11
7	6	5
8	7	1
9	8	1
10	9	0
		100

Требуется: Оценить следующие характеристики процесса поступления сообщений.

1. 
   Рассчитать эмпирические вероятности распределения числа вызовов на интервале длительностью t = 15 мин.
   
2. 
   Рассчитать среднее статистическое значение числа вызовов в интервале t=15 мин.
   
3. 
   Рассчитать вероятности распределения Пуассона P_k на интервале t=15 мин.
   
4. 
   Рассчитать число степеней свободы r и меру расхождения ² между теоретической вероятностью P_k и эмпирической
   
5. 
   Определить соответствие эмпирического распределения числа сообщений в интервале t=15 мин распределению Пуассона
   

Решение

Эмпирические вероятности распределения числа вызовов рассчитываются по формуле



Среднее статистическое значение

, где n – число интервалов наблюдения.

№ п/п	ck	nk
1	0	5	0,05
2	1	15	0,15
3	2	22	0,22
4	3	23	0,23
5	4	17	0,17
6	5	11	0,11
7	6	5	0,05
8	7	1	0,01
9	8	1	0,01
10	9	0	0
Сумма		100	1

= 2,96

Значения вероятностей распределения Пуассона могут быть определены по справочным таблицам или рассчитаны по формуле

k	Pk(t)
1	0,1534
2	0,2270
3	0,2240
4	0,1657
5	0,0981
6	0,0484
7	0,0205
8	0,0076
9	0,0025
10	0,0007

Число степеней свободы для данной задаче определяется как

r = m – 2 = 10 – 2 = 8

Мера расхождения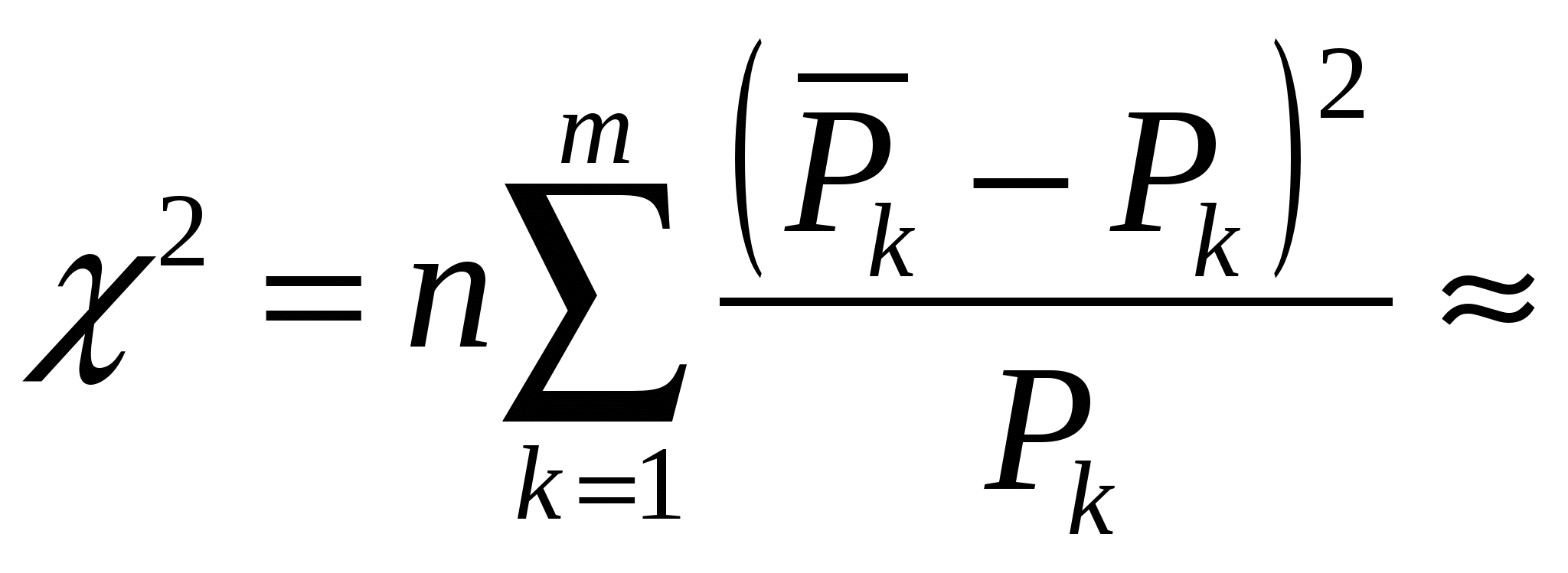

31

Из таблицы P(r, ²) = 0,70

Задача 4.
Для телефонной сети с семизначной нумерацией, полностью построенной на координатных АТС, проектируется новая координатная АТС. Рассматриваемая первая ступень группового искания комплектуется из односвязных (f=1) двухзвенных коммутационных блоков. Звено А каждого блока содержит к_a коммутаторов по n_a входов и m_a=k_b×f выходов, звено B – k_b коммутаторов по n_b=k_a×f входов и m_b выходов. Требуемое число входов проектируемой ступени – N; средняя длительность занятия входа – t_вх. Средняя длительность занятия маркера ступени – h=0.66c. На ступень поступает нагрузка y_вх. Нагрузка распределяется по направлениям. Доступности в направлениях равны d₁, d₂,…, d_r. Доли нагрузки в направлениях составляют – k₁, k₂…., k_r (Σk_i=1). Допустимые вероятности потерь не должны превышать P₁, P₂,…, P_r. Обслуживание осуществляется по системе с потерями.

Исходные данные

y_вx =550 Эрл

t_вх =80 с

N =720

к_a =4

n_a =15

k_b =20

m_b=20

m_a =20

n_b =4

Номер направления	di	ki	pi
1	40	0.09	0.005
2	40	0.09	0.005
3	40	0.06	0.005
4	40	0.07	0.005
5	40	0.10	0.005
6	40	0.11	0.005
7	40	0.04	0.005
8	20	0.04	0.001
9	20	0.05	0.001
10	20	0.10	0.005
11	20	0.08	0.005
12	20	0.05	0.005
13	20	0.12	0.005

Требуется

1. 
   Определить объем коммутационного оборудования первой ступени группового искания:
   

• 
  число блоков ступени s;
  
• 
  число линий в каждом направлении v₁, v_2,…, v_r при заданных величинах вероятностей потерь;
  
• 
  число нагрузочных групп g для каждого направления.
  

2. 
   разработать и построить схему группообразования ступени группового искания, отразив:
   

• 
  число блоков ступени s;
  
• 
  значения коммутационных параметров ступени и число линий в направлениях v₁, v_2,…, v_r.
  

3. По результатам расчетов построить графическую зависимость удельной нагрузки, поступающей на одну линию пучка в направлении c (с=y/v) от ёмкости пучка линий v при фиксированной доступности d и заданном качестве обслуживания P – c=f(v) при d=const, P=const.

Определение объема коммутационного оборудования первой ступени группового искания
Число коммутационных блоков ГИ определяется числом заданных входов N рассчитываемой ступени искания:

s=N/(n_a×k_a)

s=720/(15×4)=12

Объём коммутационного оборудования ступени определяется по расчетному значению нагрузки y_р, обеспечивающему требуемое качество прохождения нагрузки с заданной вероятностью w:

y_р=y+0.674√y, w=0.75.

Данная формула табулирована (исп. таблицу), что позволяет осуществить переход от математического ожидания к её расчетному значению и наоборот.

Отклоняясь от математического ожидания нагрузки y по эмпирическому закону, расчетное значение нагрузки y_р способствует оптимальному распределению объёма оборудования по направлениям связи. Перераспределение объёма оборудования осуществляется таким образом, что в одних направлениях имеет место надбавка, а в других скидка по отношению к объёму оборудования, вычисленному по математическому ожиданию нагрузки y. При этом суммарный объём оборудования не увеличивается, а качество обслуживания потоков вызовов, в итоге, повышается.

Нагрузка, поступающая на входы, промежуточные линии и выходы любой коммутационной системы, отличаются по своему значению и существенно зависит от длительности занятия этих элементов каждым соединением. Ввиду того, что длительность занятия промежуточных линий и выходов меньше длительности занятия входов, нагрузка y_вых на выходы ступени ГИ меньше нагрузки на входы ступени y_вх:

y_{р вых}=y_{р вх}×(t_вых/t_вх),

где t_вых и t_вх – средние длительности занятия соответственно выхода и входа ступени ГИ одним соединением.

При этом следует помнить, что t_вых меньше t_вх на среднее время t_со слушания сигнала ответа станции (t_со=3с), время приёма импульсов набора номера регистром и среднее время h занятия маркера ГИ одним соединением.
В предположении, что на проектируемой сети нет декадно-шаговых и цифровых АТС, имеем

t_вых= t_вх- t_со-t_н×n-h,

где n – число знаков номера, необходимое для осуществления соединения проектируемой координатной АТС к любой из существующих станций этой системы на сети;

t_н – время набора одного знака номера с дискового номеронабирателя (t_н=1.5 с).

t_вых=80-3-7×1.5-0.66=65,84 с

y_р=566 Эрл

y_{р вых}=566×(65,84/80)=466 Эрл

y_вых=566 Эрл

Распределение нагрузки по направлениям связи производится в соответствии с долями нагрузки k₁, k₂…., k_r в этих направлениях:

y₁= k₁× y_вых, y₂= k₂× y_вых,…, y_r= k_r× y_вых.

ЛИТЕРАТУРА

1. Лившиц Б.С., Пшеничников А.П., Харкевич А.Д. Теория телетрафика: учебник. М.: Связь, 1979

2. Мамонтова Н.П. Теория телетрафика: методические рекомендации к изучению дисциплины (спец . 200900). Заочное обучение /СПбГУТ. СПб, 2002.