Кинетическая химия. Курсовая работа.. Курсоваяработ а по физической химии химическая кинетика кинетика процессов в конденсированных фазах и на межфазовых границах
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
|
федеральное государственное бюджетное образовательное учреждение высшего образования «БУРЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. Доржи Базарова» ХИМИЧЕСКИЙ ФАКУЛЬТЕТ К У Р С О В А Я Р А Б О Т А по физической химии: химическая кинетика КИНЕТИКА ПРОЦЕССОВ В КОНДЕНСИРОВАННЫХ ФАЗАХ И НА МЕЖФАЗОВЫХ ГРАНИЦАХ СТУДЕНТ: САПОЖНИКОВА ВЕРОНИКА АНАТОЛЬЕВНА КУРС: __ III__ ГРУППА 13190 РУКОВОДИТЕЛЬ: д.х.н., проф. ХАНХАСАЕВА СЭСЭГМА ЦЫРЕТОРОВНА Улан-Удэ 2022 г. Оглавление Введение 3 Глава 1. Литературная часть. 4 1.1.Общая характеристика. 4 1.2.Факторы, влияющие на протекание химической реакции в конденсированных фазах. 5 1.3.Теория реакций в конденсированных средах. 8 Теория переходного состояния. 8 1.4.Влияние растворителя. 11 1.5.Кинетика гетерогенных процессов. 14 Плоский образец (пластинка). 16 Образец в форме шара. 16 Образец в виде цилиндра или проволки. 17 1.6.Диффузия в гетерогенных процессах. 20 Глава 2. Экспериментальная часть 25 2.1.Синтез. 25 Заключение. 26 Список литературы. 27 ВведениеИзучение любой реакции начинается с исследований кинетических закономерностей протекания реакций во времени, особенно важных для выявления механизмов Глава 1. Литературная часть.Общая характеристика.Исторически первыми процессами, исследование которых легло в основу химической кинетики, были реакции в растворах. Так, К. Гульдберг и П. Воге сформулировали закон действующих масс, обобщив результаты собственных опытов в гетерогенных системах (твёрдая фаза-раствор), и данные своих предшественников о процессах в растворах. Однако процессы в жидкости объяснить сложнее, чем в газовой фазе. Во-первых, приходится рассматривать не только молекулы реагирующих веществ, но и молекулы растворителя, во-вторых, приходится учитывать, что частицы находятся на значительно меньшем расстоянии, чем в газах, а, следовательно, сильнее взаимодействуют друг с другом. Именно поэтому кинетика сосредоточила своё внимание на процессах в газовой фазе. (булидорова) Одним из первых исследователей конденсированного состояния вещества был английский химик Гемфри Дэви, работавший в первые десятилетия XIX века. Дэви заметил, что из сорока химических элементов, известных в то время, двадцать шесть обладали металлическими свойствами, такими как блеск, пластичность и высокая электропроводность и теплопроводность. Дэви также утверждал, что элементы, которые тогда считались газами, такие как азот и водород, могут быть сжижены при соответствующих условиях и затем будут вести себя как металлы. (статья) При протекании химической реакции в конденсированной (твёрдой или жидкой) фазе возможны два варианта: Конденсированная фаза является одним из участников реакции; Конденсированная фаза является инертной средой и непосредственного участия в процессе не принимает. (булидорова) Факторы, влияющие на протекание химической реакции в конденсированных фазах.В отличие от газов, в конденсированных фазах молекулы располагаются очень близко друг от друга. Малые расстояния между частицами приводят к таким факторам как: -малая скорость движения частиц по сравнению с газами; -значительно большое число соударений частиц в единицу времени; -значительно большой роли межмолекулярных взаимодействий; -появлению «клеточного эффекта». ( булидорова) Если рассматривать разбавленные растворы двух частиц А и В в растворителе S, то в качестве первого приближения следует принять, что, раз скоро в такой системе две частицы А и В претерпит соударение, они будут находится в близком соседстве друг с другом в течении более или менее длительного времени. Среднее время жизни такой пары А – В можно грубо определить как время tAB, необходимое для того, чтобы частицы, находившиеся первоначально на расстоянии rAB друг от друга, преодолели силы притяжения и разошлись на расстояние 1,7rAB за счёт диффузии. 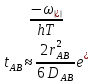 где DAB=DAS+DBS – сумма коэффициентов диффузии частиц А и В отосительно растворителя S, ωABS – энергия, необходимая для того, чтобы удалить частицы А и В друг от друга в растворителе S. Для типичных значений 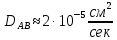 и и 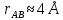 величина величина 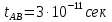 при при 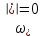 . Это примерно в 100 раз больше, чем время жизни такой же пары в газовой фазе. (бенсон) . Это примерно в 100 раз больше, чем время жизни такой же пары в газовой фазе. (бенсон)В отличие от кристалла в жидкости и в амфотерном твёрдом теле дальний порядок в расположении молекул отсутствует. Тем не менее наличие ближнего порядка и статистическое распределение различных конфигураций ядер с ближним порядком приводит к уширению уровней и образованию квазинепрерывных зон, то есть зон уровней почти сплошного спектра, хотя структура их выражена гораздо менее определённо, чем в случае упорядоченных систем. (квантовая) Так называемый клеточный эффект заключается в том, что в отличие от газовой фазы, где молекулярные фрагменты быстро разлетаются, в жидкой фазе эти фрагменты не обязательно расходятся и могут привести к повторному образованию химической связи. Это соответствует представлению о том, что достаточно плотная, конденсированная среда мешает партнёрам разойтись, удерживая их в своеобразной «клетке». Установлено, что столкновения – контакты двух выделенных партнеров – происходят сериями. При трехмерной диффузии реагентов, в момент времени t=0 разделённых расстоянием r0, вероятность хотя бы одного диффузионного контакта равна: 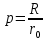 , ,где R – расстояние наибольшего сближения реагентов (равное сумме их вандервальсовых радиусов). Таким образом, данная вероятность достаточно медленно спадает с расстоянием: при любом начальном расстоянии между реагентами есть ненулевая вероятность их столкновения. Для двумерной диффузии данная вероятность равна 1 при любом начальном расстоянии между частицами. Учитывая наличие повторных контактов реагентов, говорят о том, что каждая такая серия контактов соответствует встрече реагентов в конденсированной системе (рис. 1.) (докторов)  Рис. 1. Встреча реагентов А и В в растворе. Пребывание реагентов в клетке приводит к двум результатам: Пока частицы А и В находятся на некотором расстоянии друг от друга, вероятность их столкновения в конденсированной фазе намного меньше, чем в газе. Если находившиеся в клетке частицы вступили в реакцию, то образовавшиеся частицы продуктов реакции оказываются «запертыми» в той же клетке. Окружение из молекул среды мешает им разойтись на большое расстояние, тем самым повышая вероятность обратной реакции. Это становится особенно заметным, если продуктами реакции являются активные частицы – атомы, радикалы. Таким образом, при протекании реакции распада молекул йода под действием поглощённого света (этот процесс называют фотодиссоциацией) в газовой фазе квантовый выход составляет 100%, а при проведении этой же реакции в среде четырёххлористого углерода он составляет всего 15%. Снижение выхода объясняется тем, что образовавшиеся при фотодиссоциации радикалы частично рекомбинируют в клетке. (булидорова) Теория реакций в конденсированных средах.Теория переходного состояния.Можно написать общее выражение для скорости элементарных процессов, протекание которых определяется одним потенциальным барьером. Результат скорости прохождения потенциального барьера в прямом направлении определяется выражением: 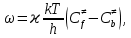 где 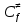 - концентрация находившихся в равновесии с реагентами активированных комплексов вдоль координаты реакции на отрезке длиной - концентрация находившихся в равновесии с реагентами активированных комплексов вдоль координаты реакции на отрезке длиной 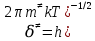 , а , а 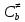 - аналогичная величина для активированных комплексов, находящихся в равновесии с продуктами, 𝜘 – коэффициент прохождения, а - аналогичная величина для активированных комплексов, находящихся в равновесии с продуктами, 𝜘 – коэффициент прохождения, а 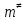 - масса активированного комплекса при его движении вдоль пути - масса активированного комплекса при его движении вдоль пути 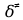 на вершине потенциального барьера. (докторов) на вершине потенциального барьера. (докторов)Образование активированного комплекса можно представить следующим образом: 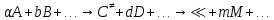 (1) (1)где 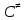 обозначает активированный комплекс, а D – промежуточный продукт реакции. Предполагается, что между активированным комплексом нет взаимодействия, поскольку в реакционном сосуде они пространственно разделены и их концентрация очень мала. Введем абсолютную активность λ, которая для идеальной системы является как отношение числа молекул в системе к функции распределения этой системы. Тогда для равновесного числа обозначает активированный комплекс, а D – промежуточный продукт реакции. Предполагается, что между активированным комплексом нет взаимодействия, поскольку в реакционном сосуде они пространственно разделены и их концентрация очень мала. Введем абсолютную активность λ, которая для идеальной системы является как отношение числа молекул в системе к функции распределения этой системы. Тогда для равновесного числа 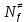 активированных комплексов, образующихся из реагентов, можно написать соотношение: активированных комплексов, образующихся из реагентов, можно написать соотношение: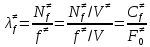 (2) (2)где 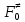 - функция распределения в единицу объёма для активированного состояния, у которой нулевой уровень отсчёта определяется нижним энергетическим состоянием реагентов. Аналогичное соотношение можно написать и для числа активированных комплексов, образуемых продуктами. Следовательно, получаем, что скорость реакции будет равна: - функция распределения в единицу объёма для активированного состояния, у которой нулевой уровень отсчёта определяется нижним энергетическим состоянием реагентов. Аналогичное соотношение можно написать и для числа активированных комплексов, образуемых продуктами. Следовательно, получаем, что скорость реакции будет равна:  , ,где 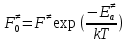 Здесь 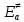 - энергия активации, а - энергия активации, а 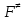 функция распределения в единице объёма для активированного комплекса, определяемая таким образом, что за нулевую энергию принимается основное состояние комплекса. функция распределения в единице объёма для активированного комплекса, определяемая таким образом, что за нулевую энергию принимается основное состояние комплекса. Общее выражение для абсолютной активности имеет вид: 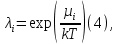 Где 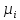 - химический потенциал, связанный со свободный энергией Гельмогольца А и свободной энергией Гиббса G соотношениями: - химический потенциал, связанный со свободный энергией Гельмогольца А и свободной энергией Гиббса G соотношениями: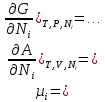 (5) (5)Применяя приближение квазистационарных концентраций к превращению реагентов в активированные комплексы, пересекающие активационный барьер в прямом направлении, находим: 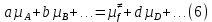 откуда с учётом соотношения (4) получаем: 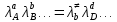 (7) (7)Аналогичное соотношение выполняется и для обратной реакции: 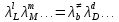 (8) (8)Для всех абсолютных активностей в качестве нулевой точки отсчёта энергии выбирается основное состояние реагентов. Используя соотношение (6) и (7), можно переписать выражение (3) следующим образом: 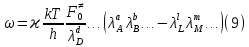 Мы получили общее выражение для скорости прямой реакции, справедливое для любых процессов в газовых, жидких или твёрдых средах. Пользуясь соотношением (4) и (5), можно представить выражение для скорости реакции в одной из двух удобных форм: 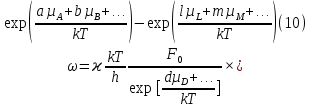 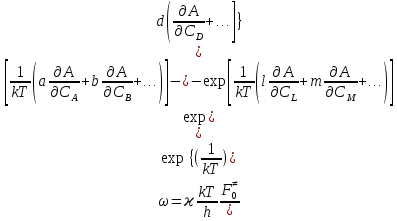 Установлено, что выражение для скорости реакции, записанные через химические потенциалы, в предельном случае малых смещений от положения равновесия приводит к обратным соотношениям Онзагера. Выражение (10) и (11) применимы не только к химической кинетике, но и ко многим другим кинетическим явлениям. Выражение (11), где скорость реакции определяется через частные производные свободной энергии Гельмгольца по концентрациям, дает полное описание кинетики реакций в растворах. (Эйринг) Влияние растворителя.Реакции, протекающие в растворах, часто плохо подчиняются теориям химической кинетики, особенно это касается полярных растворителей, интенсивно взаимодействующих с растворённым веществом. Был обнаружено, что растворитель может по-разному влиять на скорость моно- бимолекулярной реакции. Так, для многих мономолекулярных реакций переход из газовой среды в раствор не приводит к радикальному изменению скорости. В то же время бимолекулярные реакции протекают в растворах с совершенно другими скоростями, по сравнению с газами. Качественно влияние растворителя на скорость можно объяснить с использованием ранее описанной теорией переходного состояния. ( богданов) Сравним значения экспериментально определяемой константы скорости реакции n-ого порядка для реакций в растворах со значениями, полученными для тех же реакций в газовой фазе. Для простоты предположим, что газы и растворы достаточно разбавлены и все коэффициенты активности можно считать равными единице. Тогда получим: 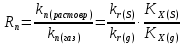 В теории переходного состояния 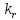 – частота колебаний или средняя частота колебаний, и с хорошей степенью приближения можно ожидать, что взаимодействие с растворителем не сильно влияет на ее величину. Таким образом, различие в скоростях реакций сводятся к различию термодинамических констант равновесия для двух фаз: – частота колебаний или средняя частота колебаний, и с хорошей степенью приближения можно ожидать, что взаимодействие с растворителем не сильно влияет на ее величину. Таким образом, различие в скоростях реакций сводятся к различию термодинамических констант равновесия для двух фаз: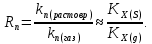 Если выразить все K в этом уравнении через равновесные концентрации двух фаз, то получим: 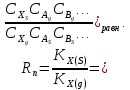 Это выражение после подстановки выражений для концентраций приводится к виду: 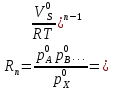 Заменим все 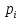 , используя уравнение Клаузиса-Клайперона, где: , используя уравнение Клаузиса-Клайперона, где: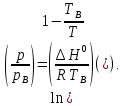 получим: 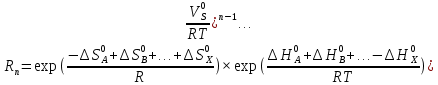 Пользуясь понятием свободного объёма для жидкости, можно написать: 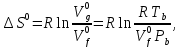 где 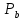 и и 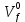 - свободный объём, приходящийся на молекулы жидкости при температуре её кипения. - свободный объём, приходящийся на молекулы жидкости при температуре её кипения. Заменяя энтропии на соответствующие свободные объёмы, получаем: 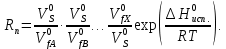 где 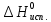 – разность между теплотами испарения продукта и реагирующих веществ. Отметим, что именно этот член уравнения оказывается зависящим от температуры, и именно он будет вызывать различия в энергиях активации процессов в двух фазах. – разность между теплотами испарения продукта и реагирующих веществ. Отметим, что именно этот член уравнения оказывается зависящим от температуры, и именно он будет вызывать различия в энергиях активации процессов в двух фазах. В случае, если энергии активации реакции в жидкой и газовой фазе одинаковы, можно привести выражение к виду: 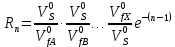 Окончательно мы имеем: 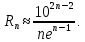 Для мономолекулярной реакции n=1, 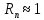 , и константы скорости практически должны совпадать для жидкой и газовой фазы, лишь в тех случаях, когда нет различий в энергиях активации процессов в двух фазах. Эти суждения применимы и в двух различным растворителям, так что для идеальных растворов следует ожидать очень слабого различия в константах скоростей при изменении растворителя. , и константы скорости практически должны совпадать для жидкой и газовой фазы, лишь в тех случаях, когда нет различий в энергиях активации процессов в двух фазах. Эти суждения применимы и в двух различным растворителям, так что для идеальных растворов следует ожидать очень слабого различия в константах скоростей при изменении растворителя. Для бимолекулярной реакции n=2, 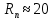 , следует ожидать, что эти реакции будут протекать несколько быстрее в растворе, чем в газовой фазе. Эти же выводы применимы к равновесию, при котором происходит изменение числа молей , следует ожидать, что эти реакции будут протекать несколько быстрее в растворе, чем в газовой фазе. Эти же выводы применимы к равновесию, при котором происходит изменение числа молей 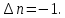 (бенсон) (бенсон)Рассмотрим влияние ионной силы раствора на реакции между ионами. Согласно теории переходного состояния, константы скорости для реакций между ионами должны зависеть от ионной силы раствора приблизительно также, как от Кинетика гетерогенных процессов.Гетерогенные процессы – это процессы, протекающие на границе двух фаз. В гетерогенных реакциях между реагирующими веществами имеется поверхность раздела. Например, при реакции между твёрдым веществом и газом поверхностью раздела является поверхность твёрдого вещества, соприкасающегося с газом. Для системы жидкость – жидкость поверхность их раздела – поверхность соприкосновения между двумя несмешивающимися жидкостями. Все гетерогенные реакции делятся на пять видов реакций по характеру поверхности раздела: твёрдое тело – газ; твёрдое – жидкость; твёрдое – твёрдое; жидкость – газ; жидкость – жидкость. В таблице 1 приведены примеры различных видов гетерогенных реакций. Таблица 1. Примеры гетерогенных некаталитических реакций.
Одной из особенностей гетерогенных процессов является зависимость их протекания от размеров и состояний поверхности раздела фаз, а также от скорости их относительного движения.(богданов) Поскольку в гетерогенных реакциях взаимодействующие молекулы переносятся из одной фазы в другую, то скорость переноса будут зависеть от площади поверхности раздела. Поэтому, очевидно, в реакциях с твёрдыми телами мелкие частицы будут реагировать быстрее, чем крупные, так как у мелких частиц площадь поверхности раздела больше. В системе жидкость – газ, жидкость – жидкость две фазы обычно хорошо смешиваются, так что образуются небольшие пузырьки газа или маленькие капельки жидкости, при этом скорость реакции увеличивается. Форма твёрдого вещества, вступающего в реакцию с жидкостью или газом, играет важную роль в определении скорости процесса. Если твёрдое вещество имеет форму пластинки или диска, то площадь поверхности в течение реакции будет неизменной, поэтому скорость реакции будет постоянной. При условии пренебрежения реакции на торцах. Если образец имеет форму цилиндра или шара, то по мере протекания реакции площадь поверхности и соответственно скорость реакции будет меняться. Рассмотрим реакцию системы твёрдое тело – жидкость, например, растворение металла в кислоте. Допустим, что концентрация кислоты остается постоянной в течение всей реакции, тогда: 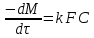 , (12) , (12)где М – масса твёрдого тела в момент времени 𝜏; F – площадь его поверхности; C – концентрация кислоты; k – константа скорости. Отрицательный знак показывает на убывании массы при растворении. При изменении геометрии твёрдого тела получаются различные кинетические уравнения. (портал) Плоский образец (пластинка).Площадь поверхности будет постоянна в течении всего процесса растворения: 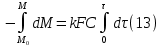 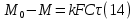 Следовательно, график зависимости 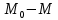 от 𝜏 должен быть прямой линией с наклоном равным kFC, из которого можно вычислить k. от 𝜏 должен быть прямой линией с наклоном равным kFC, из которого можно вычислить k.Образец в форме шара.Площадь поверхности будет убывать по времени: 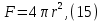 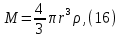 где r – радиус, а 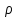 – плотность. – плотность.Следовательно, 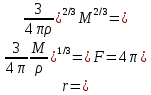 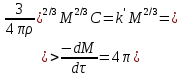 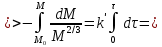 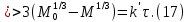 А значит, график зависимости 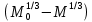 от 𝜏 или от 𝜏 или 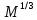 от 𝜏 должен быть прямой линией. от 𝜏 должен быть прямой линией. Образец в виде цилиндра или проволки.Пренебрегая реакцией на концах и считая длину цилиндра или проволки l=const, получим следующие уравнения: 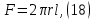 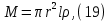 Следовательно, 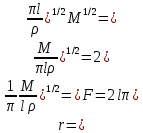 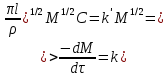 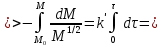 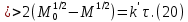 А значит, график зависимости 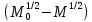 от 𝜏 или от 𝜏 или 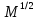 от 𝜏 должен быть прямой линией. от 𝜏 должен быть прямой линией. Образец в форме куба. В этом случае используем уравнения: 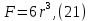 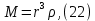 где r – длина ребра куба, а 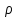 - плотность. - плотность.Следовательно, 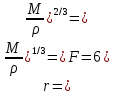 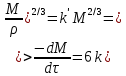 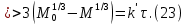 Получаем уравнение такое же, как для шара (17).(ПОРТАЛ) Другая особенность заключается в многостадийности процессов. Кроме основного процесса, протекающего на самой поверхности раздела фаз, обязательны стадии, обеспечивающие подвод к этой поверхности исходных веществ и отвод от неё продуктов реакции. Поскольку эти реакции протекают последовательно одна за другой, то скорость суммарного процесса определяется наиболее медленной стадией. Если скорость процесса определяется химическим взаимодействием на поверхности, то говорят, что реакция протекает в кинетической области. Если же лимитирующая стадия – подвод реагирующих веществ в зону реакций за счёт диффузии, то считается, что реакция протекает в диффузионной области. (иртюго) Диффузионный слой образуется, когда в состав обеих фаз входят заряженные частицы (ионы, электроны, молекулы). Диффузионный слой, состоящий из неподвижной газовой пленки, существует между твердым веществом и газом или между жидкостью и газом. Диффузионный слой, состоящий из неподвижной жидкостной пленки, имеет место между двумя несмешивающимися жидкостями, а твердый диффузионный слой – между двумя твёрдыми веществами (слой продуктов реакции, постепенно возрастающий со временем). Диффузия в гетерогенных процессах.Диффузия имеет большое значение в гетерогенных процессах, протекающих в многокомпонентных системах. При этом происходит изменение концентраций в поверхностном слое и в объёмной фазе. Диффузия – это процесс выравнивания концентраций вещества во всём объёме раствора за счёт броуновского движения частиц. Скорость диффузии зависит от плотности и вязкости среды, температуры, природы диффундирующих частиц, воздействия внешних сил и так далее. Скорость диффузии может быть определена из уравнения первого закона Фика, которое показывает, что количество вещества dm, продиффундированного за время d𝜏 через площадь S, пропорционально изменению концентраций за единицу расстояния или градиенту концентраций dC/dx: 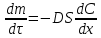 где D – коэффициент пропорциональности(коэффициент диффузии), зависящий от природы газа или растворённого вещества и температуры. Он показывает число молей, проходящих в 1 секунду через площадь в 1 см2, при падении концентрации (градиента) в 1 моль на каждый сантиметр. Знак минус в этой формуле показывает, что процесс диффузии направлен в сторону понижения концентрации. Второй закон Фика устанавливает зависимость концентрации от времени для фиксированного сечения: 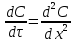 Диффузия имеет стационарный характер, когда концентрация изменяется только с расстоянием и не зависит от времени: 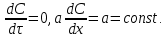 После интегрирования получаем: 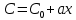 Отсюда следует, что при стационарной диффузии наблюдается линейное изменение концентрации вдоль направления диффузии, а градиент концентрации может быть записан с помощью конечных величин: 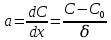 Тогда скорость стационарно диффузии: 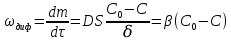 где β – коэффициент массопередачи. Рассмотрим химическую реакцию, которая имеет первый порядок и протекает стационарно. Предположим, что в этом процессе можно выделить лишь две последовательные стадии: собственно химическую реакцию и процесс диффузии. Который обеспечивает необходимый транспорт реагентов к поверхности. Вследствие стационарности данного процесса на поверхности раздела фаз не происходит накопления исходных веществ или продуктов, поэтому скорости обеих стадий одинаковы ( 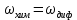 ). ).Из условия стационарности находим, что: 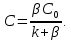 Подставив это значение в выражение скорости реакции, получим: 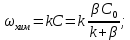 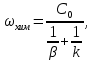 где 1/β – диффузное сопротивление, 1/k – химическое сопротивление. В случае когда k>>β, скорость реакции равна βС0 и определяется лишь величиной β, характеризующей диффузию, в случае когда k<<β, скорость реакции равна kC0, то есть скорость суммарного процесса определяется химической стадией. В ряде случаев гетерогенные процессы связаны с растворением твёрдых тел и газов в жидкости и с образованием новых фаз. Скорость растворения твёрдых веществ в жидкостях, когда объём раствора не очень велик, может быть определено по методу Щукарёва уравнением константы скорости растворения первого порядка: 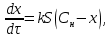 где 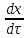 - скорость растворения в молях за время 𝜏, k – константа скорости растворения, S – площадь поверхности раздела, Cн – концентрация насыщенного раствора, x – количество растворённого вещества за время 𝜏. - скорость растворения в молях за время 𝜏, k – константа скорости растворения, S – площадь поверхности раздела, Cн – концентрация насыщенного раствора, x – количество растворённого вещества за время 𝜏.Интегрируя это уравнение, получаем: 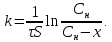 В соответствии с этой формулой скорость растворения тем больше, чем больше площадь поверхности соприкосновения фаз и разности между максимально возможной концентрацией и достигнутой в данный момент времени. Нернст предположил, что жидкость возле поверхности твёрдого тела образует особый, так называемый диффузионный слой толщиной ẟ, за пределами которого при хорошем перемешивании концентрация всюду поддерживается одинаковой. Кроме того, он считал, что скорость самого растворения значительно больше скорости диффузии, поэтому непосредственно у самой поверхности твёрдого тела раствор близок к насыщенному. Графически изменение концентрации растворённого вещетва в растворе представлено на рисунке 2. 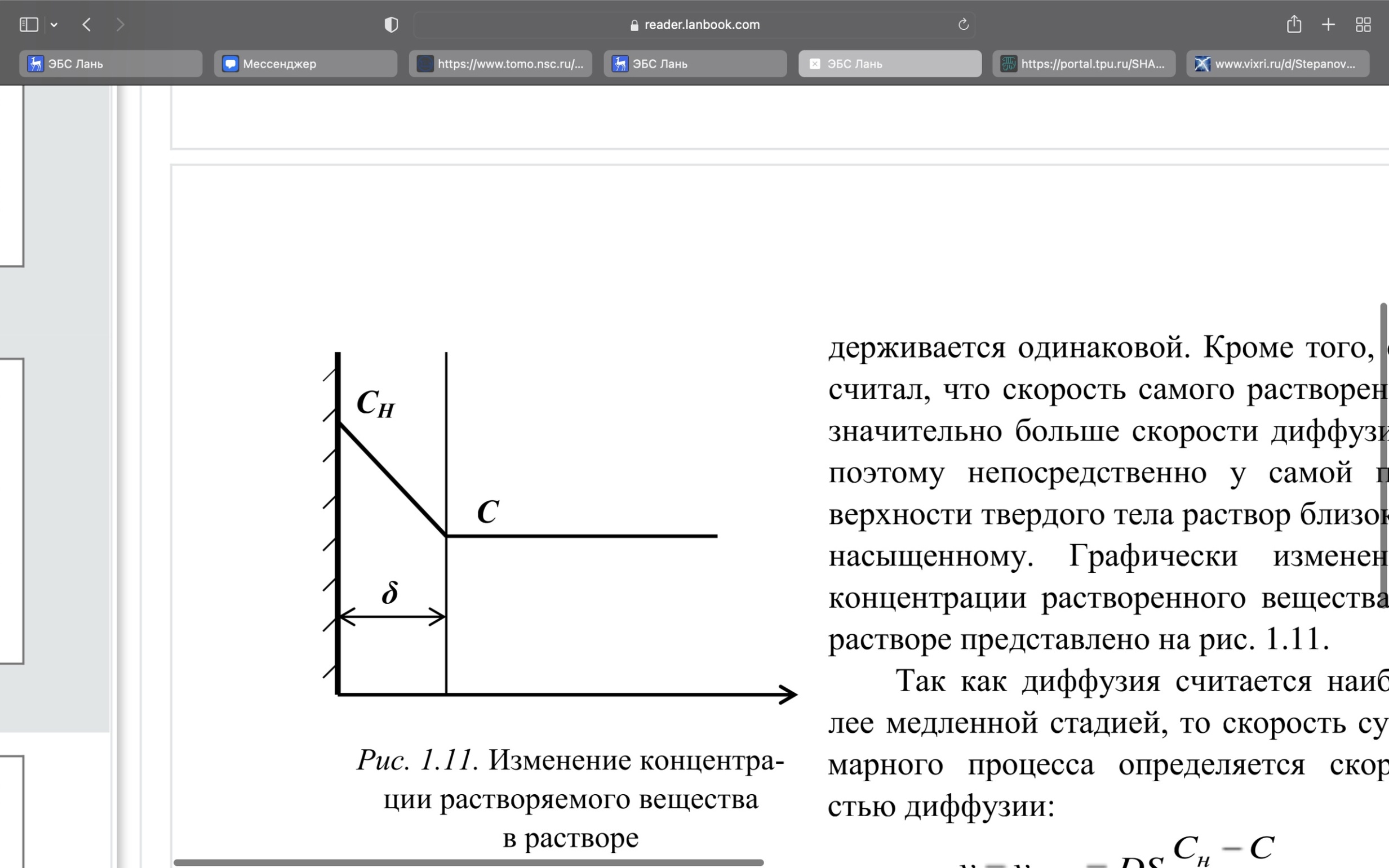 Рис. 2. Изменение концентрации растворяемого вещества в растворе. Так как диффузия считается наиболее медленной стадией, то скорость суммарного процесса определяется скоростью диффузией: 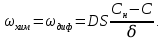 Процесс растворения газа в жидкости по сравнению с растворением твёрдого тела отличается тем, что у поверхности раздела фаз возникают два диффузионных слоя. Один из них примыкает к поверхности раздела со стороны газовой фазы, а другой – со стороны жидкости. Диффузионный слой, расположенный в газовой фазе, обеспечивает подвод к поверхности жидкости компонентов газовой фазы. Переход этих компонентов в глубину объёма жидкой фазы обеспечивается диффузионным слоем в жидкости. В зависимости от соотношений скоростей диффузий в этих слоях суммарный процесс может лимитироваться в одном из слоёв или определяться обоими слоями. Перенос вещества между поверхностью раздела фаз и их вутренним учаасткам обеспечивается не толкьо молекулярной диффузией, но и конвекцией, связанной с движением слоёв веществ. Поэтому теория Нернста не вполне соотвествует действительности. Следовательно распределение концентрации у поверхности раздела фаз не подчиняется линейному закону, как показано на рисунке 2. Диффузия у поверхности реальных твёрдых тел зависит от её шероховатости. Кроме внешней диффузии, происходящей в прилегающем к твёрдому телу слое жидкости или газа, происходит внутренняя диффузия в порах поверности. Характер внутренней диффузии определяется количеством, размером и формой пор. Глава 2. Экспериментальная частьСинтез.Заключение.Список литературы.Вольнов И.И., Пероксидные соединения щелочных металлов. – М.: Изд-во «Наука», 1980. –159с. Карякин Ю.В., Ангелов И.И., Чистые химические вещества. Изд. 4-е, пер. и доп. М.: Изд-во «Химия», 1974. – 408 с. Кнунянц И. Л., Химическая энциклопедия: В 5 Т. Под ред. Кнунянца И. Л. Том 3. – М.: Изд-во«Российская энциклопедия», 1988. – 641 с. Коттон Ф., Уилкинсон Дж. Основы неорганической химии. – М.: Изд-во «Мир», 1979. - 677с. Н.Г. Ключников. Неорганический синтез: учеб.пособие для студентов пед. ин-тов по хим. и биол. спец. – 2-е изд., перераб. – М.: Просвещение, 1998. – 240 с.: ил. Ремми Г., Курс неорганической химии. В 2 Т. Перевод с немецкого XI издания. Под ред. А.В. Новоселовой. Т. 1. – М.: Издательство иностранной литературы, 1963. – 921 с. Спицын В. И., Мартыненко Л. И. Неорганическая химия. Ч. 1: Учебник.-М.: Изд-во МГУ, 1991. – 480с. Третьяков Ю. Д., Неорганическая химия. Химия элементов: Учебник для вузов. В 2 книгах. Кн. II/ Ю.Д. Третьяков, Л.И. Мартыненко, А.Н. Григорьев, А.Ю. Цивадзе. – М.: Химия, 2001. – 583 с., ил. Третьяков Ю. Д., Неорганическая химия: В 3 Т. под ред. Ю.Д. Третьякова. Т.2: Химия переходных элементов: учебник для студ. высш. учеб.заведений–А.А. Дроздов, Зломанов В.П., Мазо Г.Н., Спиридонов Ф.М. – М.: Издательский центр «Академия», 2004. –368 с. Третьяков Ю. Д., Неорганическая химия: В 3 Т. под ред. Ю.Д. Третьякова. Т.3: Химия переходных элементов. Кн.1: учебник для студ. высш. учеб.заведений -А.А. Дроздов, Зломанов В.П., Мазо Г.Н., Спиридонов Ф.М. – М.: Издательский центр «Академия», 2007. – 352 с. Воробьёва А. Ф., Дракина С. И., Практикум по неорганической химии. – М.: Изд-во«Химия», 1984. – 248 с. Ключников Н. Г., Практикум по неорганическому синтезу. – М.: Изд-во «Просвещение», 1979. – 270 с. Лидин Р. А., Реакции неорганических веществ: Справочник / Лидин Р. А., Молочко В. А., Андреева Л. Л.; под ред. Лидина Р. А. – 2-е изд., перераб. и доп. – М.: Изд-во «Дрофа», 2007. – 637, [3] с. Третьяков Ю. Д., Практикум по неорганической химии/ под ред. Ю.Д. Третьякова. – М.: Издательский центр «Академия», 2004.–384 с. Металлические пероксиды [электронный ресурс] – Режим доступа: https://ru.qwe.wiki/wiki/Metal_peroxide#Transition_metal_peroxides Озониды [электронный ресурс] – Режим доступа: https://ru.qwe.wiki/wiki/Ozonide Пероксидные соединения неорганические [электронный ресурс] – Режим доступа: https://gufo.me/dict/chemistry_encyclopedia/пероксидные_соединения_неорганические Пероксиды щелочных металлов [электронный ресурс] – Режим доступа: https://chemege.ru/peroksidy/ |
