
Рис. 6.5.1.: К расчету плиты в стадии эксплуатации:
а) расчетная схема;
б) эквивалентное поперечное сечение плиты.
Величину расчетного пролета принимают из условия, что оси опор находятся на расстоянии 6 см от торцов плиты: l=11.96 - 2∙0.06=11.84 м.
Расчетная нагрузка на 1 м плиты (см. таб. 2.1.): q=4.23∙3=12.69 кН/м.
Изгибающий момент в середине пролета: М=12,69∙11,84∙11,84 / 8 =222,37 кН∙м.
Поперечная сила на опоре: Q=0.5∙12.69∙11.84=75.12 кН.
6.5.2. Расчет прочности нормальных сечений.
Действительное П- образное сечение плиты приводят к эквивалентному тавровому (рис.7.5.1.б). Средняя ширина ребра b=0.5∙(14+10)∙2=24 см.
в расчет вводят всю ширину полки, т.к. b’f=2.95 м < b+2∙l /6=0.24+2∙11.84 /6==4.187 м; h’f=0.03 м. Принимая а=4, 5 см, находят рабочую высоту сечения
h0=0.455-0.045=0.41 м.
Проверяют условие: Q <= 0.3∙φw1∙φb1∙Rb∙b∙h0 (7.5.2.),
обеспечивающее прочность бетона стенки по сжатой полосе между наклонными трещинами.
Принимая ориентировочно коэффициент поперечного армирования μw= 0.001, следовательно φw1=1+5∙αw∙Aw / (b∙Sw), φb1=1-β∙Rb. β=0.01 (тяжелый бетон).
φw1=1+5∙5.67∙0.001=1.03. φb1=1-0.01∙15.3=0.847.
Тогда 0,3∙φw1∙φb1∙Rb∙b∙h0=0.3∙1.03∙0.847∙15.3∙0.24∙0.41=0.3284 МН.
Т.к. 0,3284 МН > Q = 0.07512 МН, условие (6.5.2.) выполняется, т.е. размеры поперечного сечения плиты достаточны. Ориентировочно принимают величину предварительного напряжения арматуры с учетом всех потерь σsp=450 МПа. BR=0.51∙(1-0.5∙0.51) = 0.38.
M’f=15.3∙2.95∙0.03∙(0.41-0.5∙0.03)=0.535 МН∙м > М=0,22237 МН∙м.
Следовательно, граница сжатой зоны проходит в полке, и сечение рассчитывают как прямоугольное шириной b=b’f=2.95 м. Площадь сечения предварительно напряженной арматуры в продольных ребрах определяют без
учета ненапрягаемой арматуры. По формуле
В0= M / (Rb∙b∙h02)=0.22237 / (15.3∙2.95∙0.41∙0.41)=0.029<0.38=BR.
Сжатая арматура по расчету не нужна. По таб. 3.5 / 3 /: ξ= 0,03, v=0.985. Определяют коэффициент условий работы арматуры - γs6: γs6=2∙η-1-2∙(η-1) ∙ξ / ξr <=η.
η- коэффициент, принимаемый в зависимости от класса арматуры. η=1,15. γs6=2∙1.15-1-2∙(1.15-1)∙0.03/0.51=1.28 > η=1.15.
Принимают γs6=1.15.
Asp = (M-Rs∙As∙v∙h0) / (γs6∙Rs∙v∙h0) = (0.22237-0) / (1.15∙680∙0.985∙0.41) =
=0.001005 м 2 =10,05 см 2.
Принимаем 2ø28 А-V, Asp=12.32 см 2.
6.5.3. Расчет прочности наклонных сечений.
Необходимость постановки расчетной поперечной арматуры проверяют из условия (7.4.2.), обеспечивающего прочность плиты без развития наклонных трещин, т.е. при отсутствии поперечной арматуры. Усилие предварительного напряжения, с учетом γsp=0.9, равно Р0=0,9∙450∙0,001232=0,5 МН.
φn=0.1∙N / (Rbt∙b∙h0) < 0.5. φn=0.1∙ 0.5 / (1.08∙0.24∙0.41)=0.47 < 0.5.
Определяют величину Qb,u, принимая с=0,25∙l = 0.25∙11.84=2.96 м.
Т.к. Qb,u=1.5∙(1+0.47)∙1.08∙0.24∙0.41∙0.41/2.96=0.325 МН<φb3∙(1+φn)∙Rbt∙
∙b∙h0=0.6∙(1+0.47)∙10.08∙0.24∙0.41=0.0937 МН,
принимают Qb,u=0.0937 МН и проверяют условие (7.4.2.).
Т.к. Q= 0.07512 МН < 0.0937 МН=Qb,u, поперечная арматура по расчету не нужна. По конструктивным соображениям на приопорных участках назначают Sw1=0,15 м, т.к. при h=455 мм >450 мм, Sw <=h/3.
6.6. Определение геометрических характеристик поперечного сечения плиты.
Используют эквивалентное сечение (см. рис. 7.5.1.б) с учетом принятого количества арматуры и продольных стержней сетки, расположенной в полке.
Площадь приведенного сечения:
Ared= (2.95-0.24)∙0.03+0.24∙0.455+6.33∙0.001236+5.67∙0.0000879∙3=
=0.0813+0.1032+0.078+0.015=0.1998 м 2.
Статический момент этой площади относительно нижней грани:
Sred=0.0813∙(0.455-0.015)+ +0.1092∙0.2275+0.0078∙0.045+0.0015∙(0.4550.016)=0.061625 м 2.
Расстояние до нижней и верхней граней: Yred= 0.061625/0.1998=0.308 м;
h - Yred= 0.455-0.308=0.147 м.
Расстояние от центра тяжести приведенного сечения до центра тяжести сечения арматуры Asp и A’s: ysp= 0.308 - 0.045=0.263 м. уs= 0.455-0.308-0.016=0.131 м.
Момент инерции приведенного сечения плиты относительно ее центра тяжести: Ired=(2.95-0.24)∙0.03 3 / 12 + 0.0813∙(0.147- 0.015) 2 + 0.24∙0.455 3 / 12+0.1092∙
∙ (0.308 - 0.2275) 2 + 0.0078∙ 0.263 3 + 0.0015∙0.131 2= 0.0045795 м 4.
Момент сопротивления приведенного сечения плиты для нижней грани:
Wred,b= 0.0045795 / 0.308=0.01487 м 3,
для нижней грани: Wred,t= 0.0045795 / 0.147=0.03115 м 3.
Расстояние от центра тяжести приведенного сечения до верхней ядровой точки: an,t=0.01487 / 0.1998=0.074 м,
то же, до нижней ядровой точки: an,b=0.03115 / 0.1998=0.156 м.
Моменты сопротивления приведенного сечения плиты с учетом неупругих деформаций растянутого бетона. Если растянутая зона расположена внизу сечения, приложение нулевой линии определяют по формуле:
(2,95-0,24)∙0,03∙(х-0,015)+0,5∙0,24∙х 2+0.0015∙(x-0.016)-0.0078∙(0.41-x)=
=0.5∙(0.455-x)∙0.24∙(0.455-x), откуда х=0,147 м.
h - x= 0.308 м. По формуле при
Ib0= (2.95-0.24)∙0.033 / 12+ (2.95-0.24)∙0.03∙(0.147-0.015)2+
+ (0.24-0.1473 / 3) =0.001647 м 4.
α s∙I so=0.0078∙(0.308-0.045)2=0.00054 м 4. α s∙I’so=0.0015∙(0.147-0.016)2=0.000026 м 4.
Sbt=0.5∙0.24∙0.308∙0.308=0.01184 м 3.
Wpl,b=2∙(0.001677+0.00054+0.000026) / 0.308+0.011384=0.02595м 3.
6.7. Предварительное напряжение арматуры и его потери.
Назначают величину предварительного напряжения арматуры σsp=740 МПа. Учитывая, что допустимое отклонение ∆σsp величины предварительного напряжения арматуры при механическом способе натяжения:
∆σsp=0.05∙740=37 МПа. Т.к. σsp+∆σsp=740+37=777 МПа s,ser=785 МПа.
σsp-∆σsp=740-37=703 МПа >0.3∙Rs,ser=0.3∙785=235.5 МПа
потери предварительного напряжения арматуры определяют по таб. 2.4. / 3 /.
Потери от релаксации напряжений арматуры: σ1=0,1∙740-20=54 МПа.
Потери от температурного перепада отсутствуют, т.к. арматура и форма нагреваются в одинаковой степени, т.е. σ2 =0.
Потери от деформации анкеров, расположенных у натяжных устройств, при= l=13 м и λ = 1,25+0,15∙28=5,43 мм; σ3= 5,45∙190000:13000= 80 МПа.
Трение арматуры при натяжении отсутствует, поэтому σ4 =0.
Потери от деформации стальной формы в связи с отсутствием данных о технологии изготовления и конструкции формы принимают σ5= 30 МПа.
Сумма всех этих потерь σ5= 54+0+80+0+30=164 МПа.
Предварительное напряжение арматуры перед обжатием бетона
σsp= 740-164=576 МПа.
Усилие предварительно напряжения Ро= σsp∙Asp= 576∙0.001232= 0.71 МН.
Максимальный изгибающий момент от веса плиты:
Md= 2.09∙3∙11.842 : 8 = 109.87 кН∙м = 0,10987 МН∙м.
Максимальные сжимающие напряжения бетона от действия силы Ро определяют по формуле: σ bp= p0 / Ared ± p0∙ e0p ∙ yi / Ired ± M ∙ yi / Ired ± N / Ared . При
Мd =0 , е0р = уsp.. σbp = 0.71: 0.1998+0.71∙0.263∙0.308 : 0.0045795 = 16,1 МПа.
Поскольку Rbp=0.7∙30=21 МПа и σ bp в бетоне не превышают максимально допустимых, определяют потери от быстро натекающей ползучести бетона (см. таб. 2.6. /3/). Для этого вычисляют напряжения в бетоне на уровне центра тяжести сечения напрягаемой арматуры от действия силы Ро и изгибающего момента от веса плиты: σbp=0.71: 0.1998+0.71∙0.263: 0.0045795 ∙ 0.263 – 0.08443 : 0.0045795 ∙ 0.263=
= 9.43 МПа. Т.к.
σbp / Rbp = 9.73: 21=0.449 < α = 0.75, то σ6 = 0,85∙40∙0,449=15,3 МПа.
Следовательно, первые потери σloss= 164+15.3=179.3 МПа.
Напряжения в бетоне при обжатии на уровне центра тяжести сечения верхней (ненапрягаемой) арматуры:
σ’bp= 0.71: 0.1998- 0.71∙0.263 : 0.0045795 ∙ 0.131+ 0.08443 : 0.0045795∙0.131=
=0.63 МПа.
Напряжения в верхней арматуре от быстро натекающей ползучести
σs= 0.85∙40∙0.63 : 21 =1.02 МПа.
Усилие предварительного обжатия с учетом первых потерь:
Р01= (740-179,3)∙0,001232-1,02∙0,000264=0,6905 МН.
Потери от усадки бетона, подвергнутого тепловой обработке: σ8 = 0,85∙40=34 МПа.
Потери от ползучести бетона находят в зависимости от величины σbp / Rbp.
Для предварительно напряженной арматуры σbp / Rbp < α, поэтому
σ9 = 0,85∙150∙0,449=57,25 Мпа.
Суммарная величина потерь напряжений:
σloss = 179.3+34+57.25=270.55 МПа
271 МПа.
Напряжения в верхней (ненапрягаемой) арматуре от усадки бетона: σ’s = σ8=34 МПа, от ползучести: σ’s =0,85∙150∙0,63: 21=3,83 МПа, суммарные ( с учетом напряжений от быстро натекающей ползучести):
σ' s =1.02+34+3.83 = 38.85 МПа
39 МПа
6.8. Расчет плиты по образованию трещин.
В соответствии с таб. 2.2. /3/ для конструкций, к трещиностойкости которых предъявляют требования 3-ей категории, расчет по образованию трещин выполняют для выявления необходимости проверки по раскрытию трещин и случая расчета по деформациям. При этом следует принимать коэффициент точности натяжения арматуры γsp = 1 и коэффициент надежности по нагрузке γf=1.
Усилие предварительного обжатия с учетом всех потерь:
Р02 =(740-271)∙0,001232-39∙0,000264=0,5675 МН.
Эксцентриситет приложения усилия обжатия относительно центра тяжести приведенного сечения:
е0р = [(740-271)∙0.001232∙0.263+39∙0.000264∙0.131] : 0.5675 = 0.27 м.
Распределенная нагрузка на плиту при γf=1: q= (3.57∙1∙0.95) =3.39 кПа,
q= 3.39∙3= 10.17 кН/м
10,2 кН/м.
Изгибающий момент от этой нагрузки в середине пролета плиты:
М = 10,2 ∙ 11,842 : 8 = 178,7 кН∙м.
По формулам φ = 1,6 – σb / Rb,ser; σb=[ P02∙(an,t + an,b) + 2Rbt,ser∙Wred,b ] / Wred,t =
[0.5675∙(0.074+0.156)+2∙1.8∙0.01487] : 0.03115= 5.91 МПа.
φ= 1,6-5,91 : 22 = 1,33 > 1.
Принимаем φ=1, поэтому r=an,t. Поверяют условие Mr <= Mcrc. Т.к.
Mcrc=0.5675∙(0.27+0.074)+1.8∙0.02595=0.242 МН∙м=242 кН∙м > Mr 178.7кН∙м,
в нормальных сечениях плиты трещины не образуются, расчет по деформациям с учетом наличия трещин в растянутой зоне не выполняем.
Проверяют возможность образования верхних трещин. Усилие предварительного обжатия с учетом первых потерь Р01=0,6905 МН.
Максимальный изгибающий момент при γf = 1 веса плиты Md=109.87 кН∙м.
Образование верхних трещин проверяют по условию 4.26. /3/. Т.к.
Р01( e0p – rb) - Md = 0.6905(0.263-0.156)-0.10987= - 0.036 МН∙м < Rb,t(p),ser ∙
∙Wpl,t= 0.7∙1.8∙0.04184= 0.0527 МН∙м, верхние трещины не образуются.
Для выяснения необходимости расчета по раскрытию наклонных трещин проверяют, образуются ли такие трещины в пределах длины зоны передачи напряжений. Расчеты по образованию наклонных трещин выполняют для двух сечений плиты: у грани опоры (сечение – 1) и на расстоянии lp от торца (сечение – 11) (рис. 6.8.1.).

Рис.6.8.1.:Приопорный участок плиты покрытия.
В обоих случаях проверку осуществляют для уровня центра тяжести сечения: (y= yred= 0.308 м). Т.к. между местом приложения опорной реакции и рассматриваемым сечениями поперечной нагрузки может не быть, для обоих случаев принимают: Q= Qmax =0.5∙3∙3,390∙11,84=60,21 кН.
Определяют значение Р0 в рассматриваемых сечениях. Для этого
lp= (ω∙σs / Rbp +∆λp)∙ d, где ωр= 0,25, ∆λ=10 (таб. 5.26 /3/).
lp= (0.25∙740-179.3 : 21 + 10) ∙ 2.8=50.4 см.
Для сечения – 1 lx=12 см, в этом сечении Р102= 0,5675∙12 : 50,4 = 0,135 МН.
Для сечения – 2 lx= lp, следовательно Р1102 = 0,5675 МН.
Определяют нормативные напряжения σх на уровне центра тяжести сечения по формуле (2.13. /3/), при у= 0: σ1х= 0,135 : 0,1998 = 0,676 МПа;
σ11х = 0,5675 : 0,1998 = 2,84 МПа.
Т.к. напряжения σ1х и σ11х сжимающие, при вычислении σmt и σmс в формулу (6.8.1.) подставляют их со знаком минус:
σmt(mc) = (σx+σy) : 2 ± 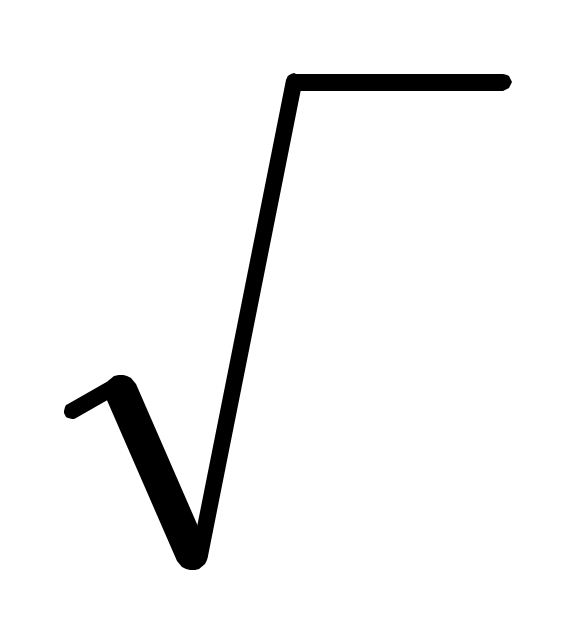 (σx – σy) : 2 +τ2xy , (7.8.1.) (σx – σy) : 2 +τ2xy , (7.8.1.)
τxy= 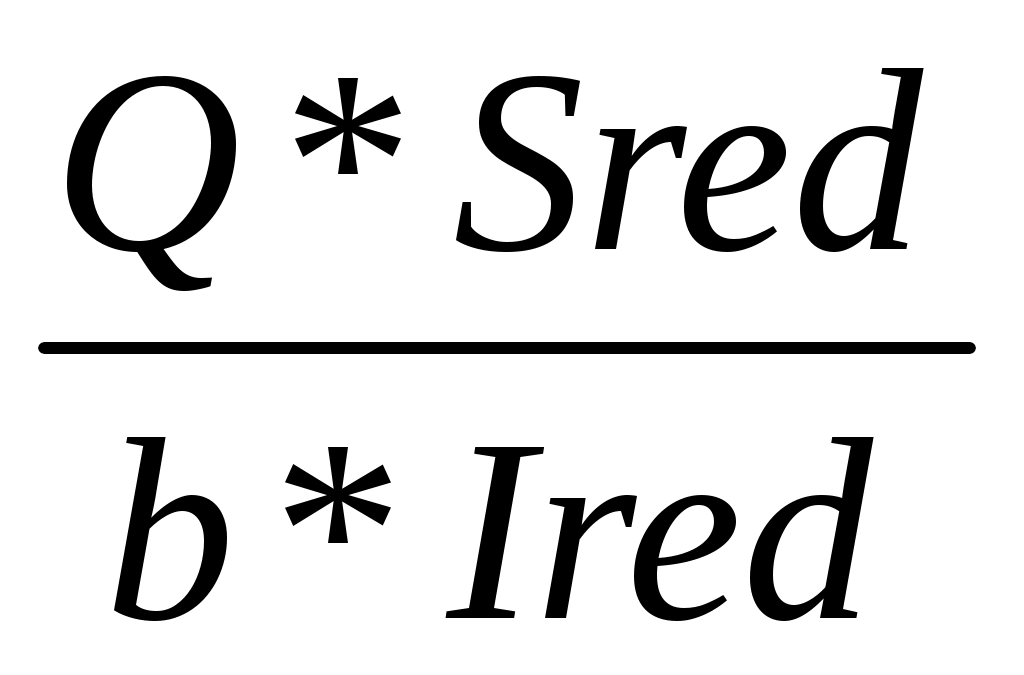 . .
Для этого вычисляют Sred, расположенный выше центра тяжести сечения, относительно нулевой линии:
Sred= (2.95-0.24)∙0.03∙0.132+0.5∙0.24∙0.1472 + 0.0015∙0.131 = 0.01352 м 3.
τ1ху= τ11ху= 0,06021∙0,01352: 0,24: 0,0045795 = 0,741 МПа.
Поскольку предварительно напряженная поперечная арматура отсутствует, σур=0. По формуле σy,loc = φy ∙ [P / ( b∙h)]
определяют местные сжимающие напряжения вблизи места приложения опорных реакции. Для сечения – 1:  α = x1: h = 0.04 : 0.455 = 0.088; α = x1: h = 0.04 : 0.455 = 0.088;
β = y : h = 0.308 : 0.455 = 0.677.
Тогда
σ1y,loc = 0.06021 : 0.24 : 0.455 ∙ 2∙ 0.6772 : 3.14 ∙ [ (3-2∙0.677) : (1+0.0882)2 -
- 0.677 : (0.0882 + 0.6772)2 ] = 0.161∙[1.621-3.117] = - 0.289 МПа.
Знак минус показывает, что напряжения сжимающие.
Для сечения – 2: α = x11 : h = 0.424 : 0.455 = 0.932 > 0.7, т.е. σ11y,loc = 0
По формуле (7.8.1.) определяют главные растягивающие напряжения.
Для сечения – 1:
σ1mt(mc) = - (0.676-0.289) : 2 ± 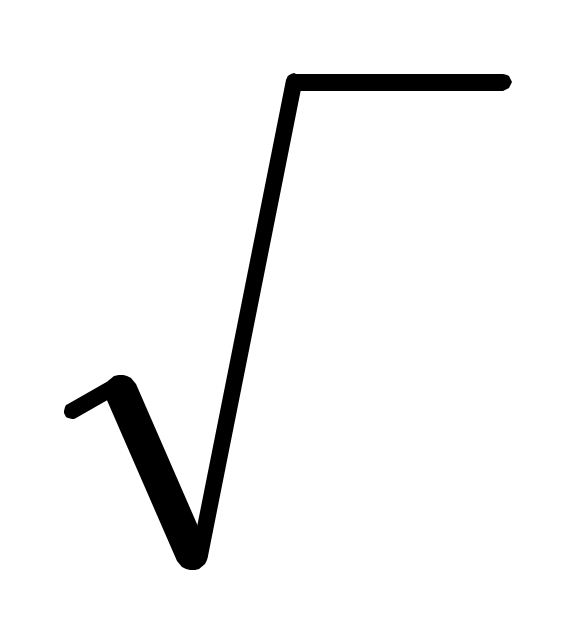 [(-0.676-0.289) : 2] 2 + (0.741)2 = [(-0.676-0.289) : 2] 2 + (0.741)2 =
=(-0.4825 ±0.8842) МПа. σ1mt = -0.4825+0.8842 = 0.40 МПа;
σ1mc = -0.4825-0.8842 = -1.32 МПа.
Для сечения – 2: σ11mt(mc) = -2.84 : 2 ± 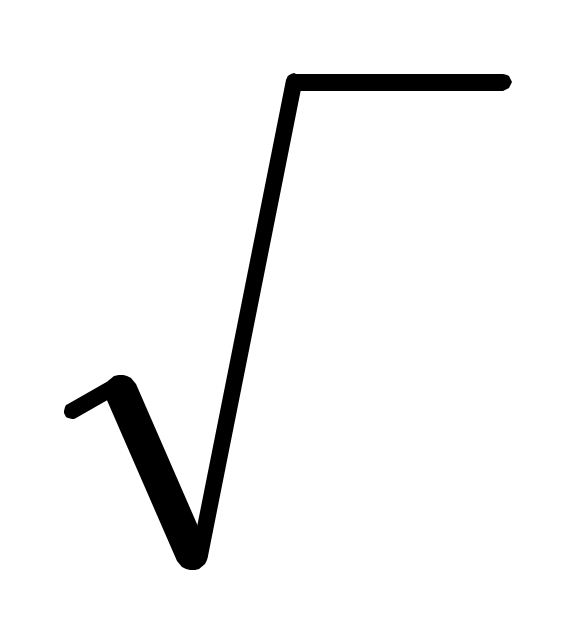 (2.84 : 2) 2 + 0.741 2 = (2.84 : 2) 2 + 0.741 2 =
= ( - 1.42 ± 1.77) МПа.
σ11mt = - 1.42 + 1.77 = 0.35 МПа; σ11mc = - 1.42 – 1.77 = - 3.19 МПа.
По таб. 4.3. / 3 / определяют коэффициент γb4, учитывающий влияние двуосного напряженного состояния на прочность бетона. Для бетона класса В30 γb4 = 0.5.
Т.к. |σmc| < γb4∙ Rb,ser = 0.5∙22=11 МПа.
Для обоих сечений σmt < Rbt,ser = 1.8 МПа, следовательно, на участке элемента в пре делах длины зоны передачи напряжений наклонные трещины не образуются.
Проверяют условие образования трещин для сечения – 3 в месте примыкания сжатой полки к ребрам. lx = 0.49 м. х111 = 0,41 м.
Р11102 = 0,5675∙49 : 50,4 = 0,5517 МН; М = Q ∙ x = 0.07512 ∙ 0.41 = 0.031 МН∙м.
σ111х = 0,5517 : 0,1998 – 0,5517 ∙ 0,27 : 0,0045795 ∙ 0,117 + 0,031∙0,117 : :0,0045795 = - 0,25 МПа.
Sred = 2.95∙0.03∙0.015+0.0015∙0.014 = 0.00135 м 3.
τ111ху = 0,07512∙0,00135 : 0,0045795 : 0,24 = 0,092 МПа.
σ111mt(mc) = 0.25 : 2 ± |
 Скачать 403.5 Kb.
Скачать 403.5 Kb.

