Проектирование активного фильтра 5 порядка. Курсовой проект дисциплина Электроника и схемотехника Наименование темы Проектирование активных фильтров
 Скачать 1.61 Mb. Скачать 1.61 Mb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Вологодский государственный университет» «Электроэнергетический факультет» «Управляющие и вычислительные системы» КУРСОВОЙ ПРОЕКТ Дисциплина: «Электроника и схемотехника» Наименование темы: «Проектирование активных фильтров» Руководитель: профессор Водовозов А.М Выполнил: студент Группа, курс Дата сдачи ___________________________________________ Дата защиты ___________________________________________ Оценка по защите___________________________________________ Вологда 2022 г. Содержание. Введение……………………………………………...…..........3 2 Техническое задание…………..…………………………….4 3 Основная часть…..……………..………..………………..…6 3.1 Основные сведения об активных ФВЧ RC фильтрах. 3.2 Расчёт 1-го звена……….…….………………………........6 3.3 Расчёт 2-го звена……….…….…………………………....8 3.4 Расчёт 3-го звена……….…….…………………………....11 3.5 Расчёт АЧХ и ФЧХ проектируемого фильтра…………..12 4.Моделирование работы фильтра..……………………...…..9 5 Заключение….…………………...……...……....…………..16 Список литературы……………………………………..……..17 Введение. Электрический фильтр – это устройство, которое пропускает без существенного влияния спектральные составляющие сигнала в заданной полосе частот и значительно ослабляет (подавляет) все спектральные составляющие вне этой полосы. Полоса частот, в которой ослабление мало, называется полосой пропускания. Полоса частот, в которой ослабление велико, называется полосой непропускания (задерживания). Между этими полосами находится переходная область. По расположению полосы пропускания на шкале частот различают следующие разновидности фильтров: ФНЧ – фильтры нижних частот; ФВЧ – фильтры верхних частот; ПФ – полосовые фильтры; РФ – режекторные (заграждающие) фильтры. В зависимости от применяемой элементной базы выделяют классы пассивных LC, кварцевых, электромеханических и других, не содержащих активных элементов – транзисторов, микроминиатюрных усилителей. В связи с блестящими успехами в области микроэлектроники были разработаны активные RC- фильтры, не содержащие громоздких индуктивностей, а использующих в качестве активных элементов транзисторы и операционные усилители. Цифровизация науки и техники вызвала появление цифровых(дискретных) фильтров. Математически свойства фильтра описываются его функцией фильтрации. В зависимости от вида функции фильтрации получают различные типы фильтров. Если в качестве функции фильтрации используют полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров широкое использование нашли фильтры Баттерворта и Чебышева. Если функция фильтрации – дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева - Кауэра. 2.Техническое задание. Требуется спроектировать активный RC фильтр верхних частот 5-го порядка на операционных усилителях, используя звенья второго порядка по схеме Рауха (с многопетлевой обратной связью) и звенья первого порядка на инвертирующем ОУ. Параметры фильтра заданы в таблице 2.1 Таблица 2.1
3. Основная часть 3.1 Основные сведения об активных ФВЧ RC фильтрах. Для математического описания свойств фильтров используется передаточная функция H(p) = 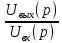 = = 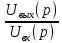 . Для установившихся сигналов передаточную функцию можно выразить в виде комплексного коэффициента передачи H(jω) = |H(jω)|* . Для установившихся сигналов передаточную функцию можно выразить в виде комплексного коэффициента передачи H(jω) = |H(jω)|*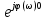 , где |H(jω)| - АЧХ, φ(ω) – ФЧХ фильтра. , где |H(jω)| - АЧХ, φ(ω) – ФЧХ фильтра.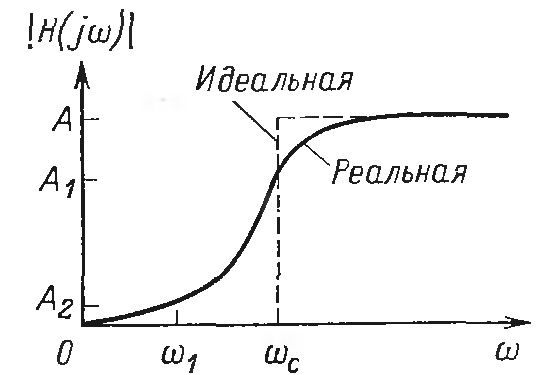 Рис.1.Идеальная и реальная АЧХ ФВЧ. Идеальный ФВЧ имеет прямоугольную АЧХ, но реализовать её невозможно, поэтому передаточная функция реализуемых фильтров отличается от идеальной и представляет из себя отношение некоторых двух функций. Очень часто эти функции представляют из себя отношение двух полиномов: H (p) =  , где a и b – действительные постоянные числа. Степень полинома знаменателя n - определяет порядок фильтра. , где a и b – действительные постоянные числа. Степень полинома знаменателя n - определяет порядок фильтра. При различных способах оптимизации (аппроксимации) передаточных характеристик фильтров – по Баттерворту, Чебышеву, Бесселю – необходимо знать значения коэффициентов A, B, C ( или ai, bi ) чтобы получить нужный способ оптимизации передаточной характеристики. Эти значения берутся из справочников по расчёту фильтров, Активные фильтры на операционных усилителях –ARC-выполняются по каскадной схеме, содержащей несколько последовательно включённых звеньев, когда выход первого звена является входом второго и т. д.Поскольку операционный усилитель обладает практически бесконечным входным и нулевым выходным сопротивлениями, то звенья не влияют друг на друга и не изменяют собственные передаточные функции. Таблица 2.2
Распределяем равномерно усиление по каскадам фильтра: К01 = К02 = К03 = 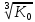 = = 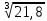 ≈ 2, 794 раз. ≈ 2, 794 раз.Выбираем структуру фильтра:  Рис.2.Структура проектируемого ФВЧ. 3.2 Расчёт 1-го звена. При правильно выбранных коэффициентах ai, bi передаточной характеристики не имеет значения в каком порядке будут включены звенья фильтра: итоговая частотная характеристика будет одна и та же. 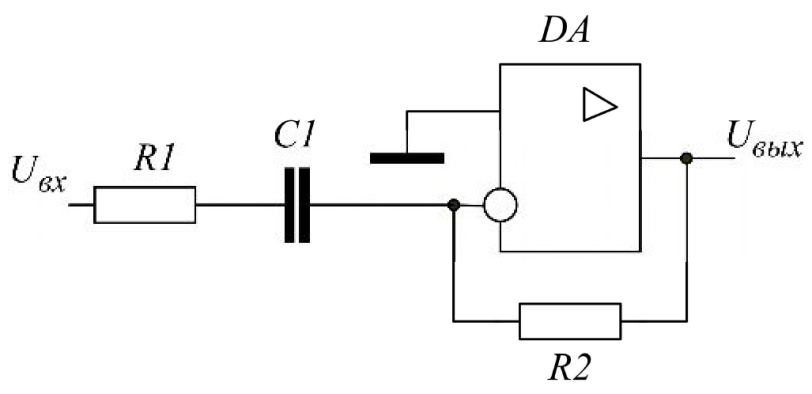 Рис.3. ФВЧ первого порядка на основе инвертирующего усилителя. Нормированная передаточная функция фильтра рисунке 3 имеет вид Л1.стр.12: W1 (p) = -  K0 = 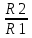 = K0 = 2, 794; a1 = = K0 = 2, 794; a1 = 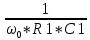 = 5, 6334 – Л.5. стр.198 = 5, 6334 – Л.5. стр.198ω0 = 2*π*F0 = = 2*3, 14159*8190 ≈ 5, 1459*104 рад/c. Для построения звеньев фильтра выбираем операционный усилитель OP249, который имеется в библиотеке схемотехнического симулятора MultiSim. Основные параметры ОУ OP249
Исходя из этих параметров определяем диапазон возможных значений параметров элементов в схемах каскадов фильтра.Rmin > 10*Rвых = = 35*10 = 350 Ом; Rmax < 10*Rвх = 1012/10 = 1011 Ом; F0 < fТ / 10 = 4, 7*106 / 10 = 470000 Гц. Ёмкости конденсаторов рекомендуется (Л2.стр.15) выбирать порядка С ≈ 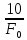 мкФ = мкФ =  = 0, 00122 мкФ = 1, 22 нФ. Предпочтительно при расчёте = 0, 00122 мкФ = 1, 22 нФ. Предпочтительно при расчётеai , bi задаваться величиной ёмкости, а не сопротивления, так как стандартный ряд ёмкостей значительно короче стандартного ряда сопротивлений- Л.1.стр.18. Для более точной реализации передаточной функции величины R и C должны быть как можно ближе к значениям стандартного ряда значений. Для этого просчитаем значения R1, задаваясь значением С1 из стандартного ряда согласно Л1.стр.18. R1=  = =  . Результаты . Результаты в таблице 3. Таблица 3
Наилучшее приближение к стандартным значениям имеет пара С1= 0, 56 нФ и R1 = 6157 Ом, поэтому задаёмся С1 = 0, 56 нФ = 560 пФ и R1 = 6, 2 кОм = 6200 Ом.R2 = K01*R2 = 2, 794*6200 = 17, 333 кОм. Выбираем ближайшее стандартное значение R2 = 18 кОм, фактический К01 = R2 / R1 = 18/6,2 = 2, 9032 раз. Передаточная функция каскада W01 (p) = -  = - = -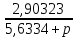 . .Находим комплексный коэффициент передачи при p = j*ω: W01 (jΩ) = -  , где Ω = , где Ω =  - нормированная частота. - нормированная частота.Зависимость модуля этой функции от нормированной угловой частоты и есть нормированная АЧХ - амплитудно-частотная характеристика первого каскада. Она изображена на рис.4 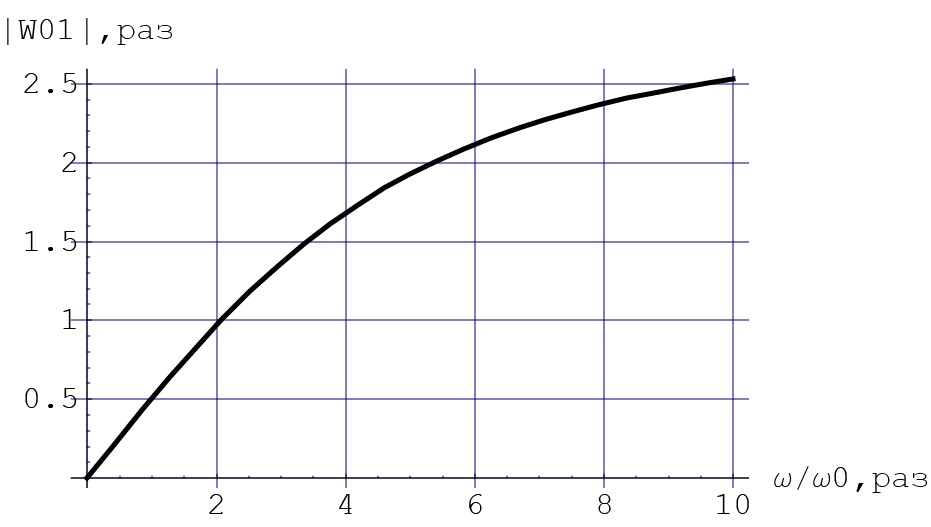 Рис.4.Теоретическая АЧХ первого звена фильтра. 3.3 Расчёт 2-го звена. По заданию второе звено должно быть спроектировано по схеме Рауха (схема с многопетлевой обратной связью). Схема ФВЧ Рауха второго порядка содержит кроме операционного усилителя три конденсатора и два резистора. 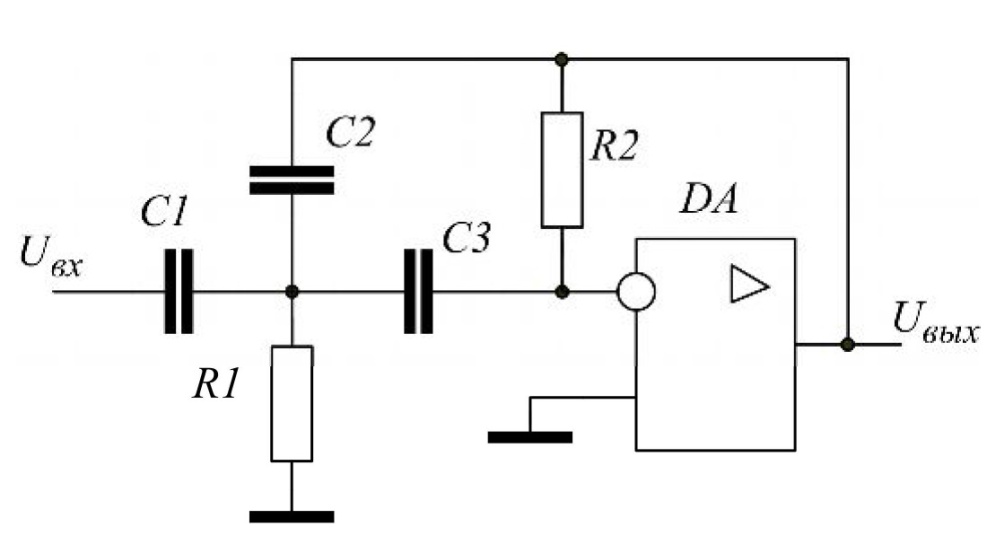 Рис.5.Схема ФВЧ Рауха второго порядка. Нормированная передаточная функция звена рисунке 5 имеет вид Л1.стр.13: W02 = -  = - = - 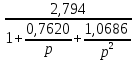 K0 =  = 2, 794; a2 = = 2, 794; a2 =  = 0, 7620; b2 = = 0, 7620; b2 = 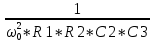 = 2, 6530. = 2, 6530.Для более точной реализации передаточной функции величины R и C должны быть как можно ближе к значениям стандартного ряда значений. Задаёмся значением С2 ≈ 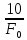 мкФ = мкФ =  1, 2 нФ = 1, 2*10-9 Ф. Определяем величину 1, 2 нФ = 1, 2*10-9 Ф. Определяем величину C1 = K0*C2 = 2, 794*1, 2*10-9 = 3, 3528*10-9 Ф, задаёмся С1= 3, 3 нФ = 3300 пФ. Теперь задаваясь значениями С3 из стандартного ряда в диапазоне С3 = 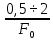 = 0, 56 нФ ÷ 2, 4 нФ найдём пары значений R1 и R2: = 0, 56 нФ ÷ 2, 4 нФ найдём пары значений R1 и R2:R2 = 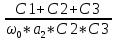 = = 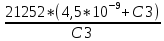 R1 =  = = 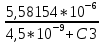 Результаты расчётов по выбору С3, R1, R2 представлены в таблице 3.1 Таблица 3.1
Из таблицы 3 выбираем самое оптимальное сочетание значений С3, R1, R2: С3= 0, 68 нФ = 680 пФ, R1 = 1, 1 кОм, R2 = 160 кОм. K02 =  = =  = 2, 75 раз. = 2, 75 раз.Проверяем фактические параметры передаточной функции второго каскада: a2 =  = = 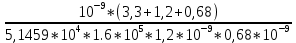 = 0, 771 = 0, 771 – отличается на +1, 18%. b2 = 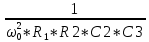 = =  = 2, 6295- отличается на = 2, 6295- отличается на-0, 89 %. Такая точность является очень хорошей для инженерной практики. Нормированная передаточная функция W02 (p) = - 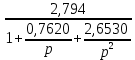 В частотной области: p = j*ω W02 (jω) =  График модуля этой комплексной функции представлен на рис.6 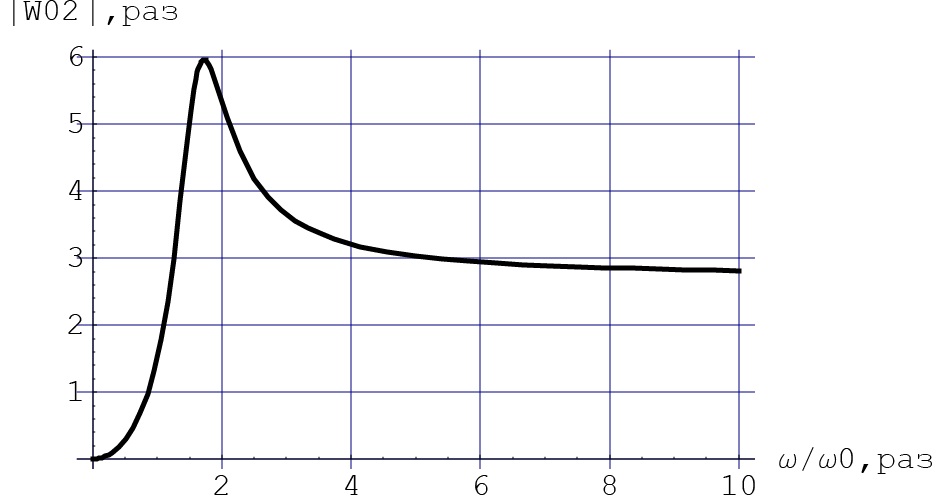 Рис.6.Теоретическая АЧХ второго звена фильтра. 3.4 Расчёт 3-го звена. Схема третьего каскада фильтра будет отличаться от второго звена только параметрами элементов. Уточняем величину коэффициента усиления третьего каскада: K03 =  = = 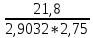 = 2, 731 раз, берём с запасом K03 = 3. = 2, 731 раз, берём с запасом K03 = 3.Параметры передаточной характеристики: a3 = 0, 1172; b3 = 1,0686. Задаёмся значением С2 =10 пФ = 1, 1*10-9 Ф. Определяем величину C1 = K0*C2 = 3*1, 0*10-9 = 3000*10-12 Ф, задаёмся С1= 3300 пФ. Теперь задаваясь значениями С3 из стандартного ряда в диапазоне 300 ÷ 3000 пФ найдём пары значений R1 и R2: R2 = 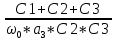 = =  R1 = 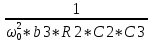 = = 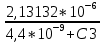 Таблица 4
Из таблицы 4 выбираем самое оптимальное сочетание значений С3, R1, R2: С3= 470 пФ, R1 = 430 Ом, R2 = 1,6 МОм. Проверяем фактические параметры передаточной функции третьего каскада: K03 =  = =  = 3 раз. = 3 раз.a3 =  = = 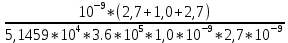 = 0, 1157 = 0, 1157b3 = 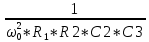 = =  = 1, 0407 = 1, 0407Нормированная передаточная функция W03 (p) = -  В частотной области: p = j*ω W02 (jω) =  График модуля этой комплексной функции представлен на рис.7  Рис.7.Теоретическая АЧХ третьего звена фильтра. 3.5 Расчёт АЧХ и ФЧХ проектируемого фильтра Передаточная функция каскадной схемы равна произведению передаточных функций всех звеньев: W (p) = W (p)* W2* W3 (p) = - 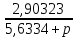 *- *- 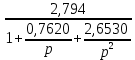 *- *-  = =W (jω) =   Рис.8.Теоретическая АЧХ фильтра.  Рис.9.Теоретическая ФЧХ фильтра. 4.Моделирование работы фильтра 4.1 Измерение АЧХ и ФЧХ фильтра в симуляторе MultiSim. 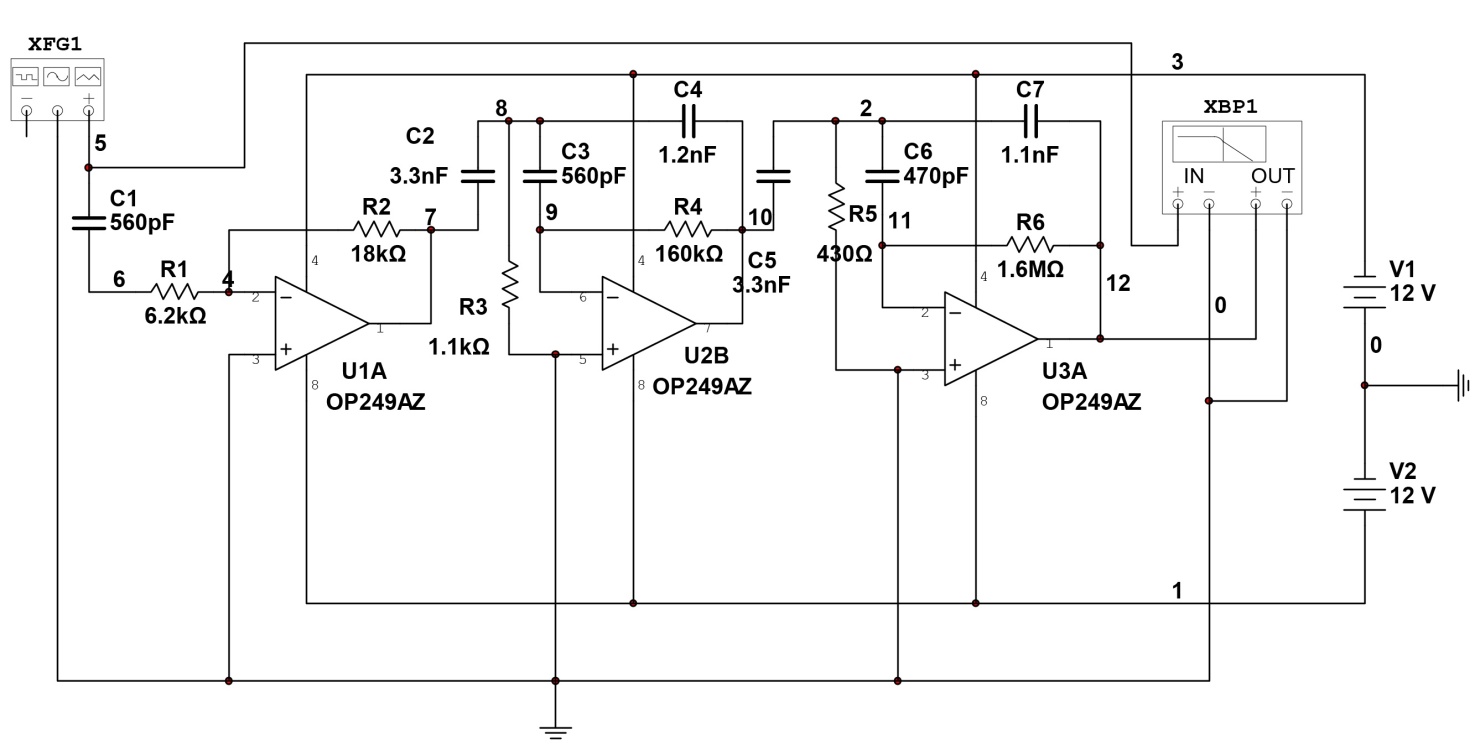 Рис.10.Схема проектируемого ARC фильтра в симуляторе MultiSim 10.  Рис.11.Вид АЧХ в симуляторе MultiSim 10.  Рис.12. Вид ФЧХ в симуляторе MultiSim 10. Сравнивая рис.8, 9 и рис.11, 12 можно сделать вывод, что результаты теоретического расчёта совпадают с результатами моделирования. 4.1 Измерение переходной характеристики фильтра в симуляторе MultiSim. 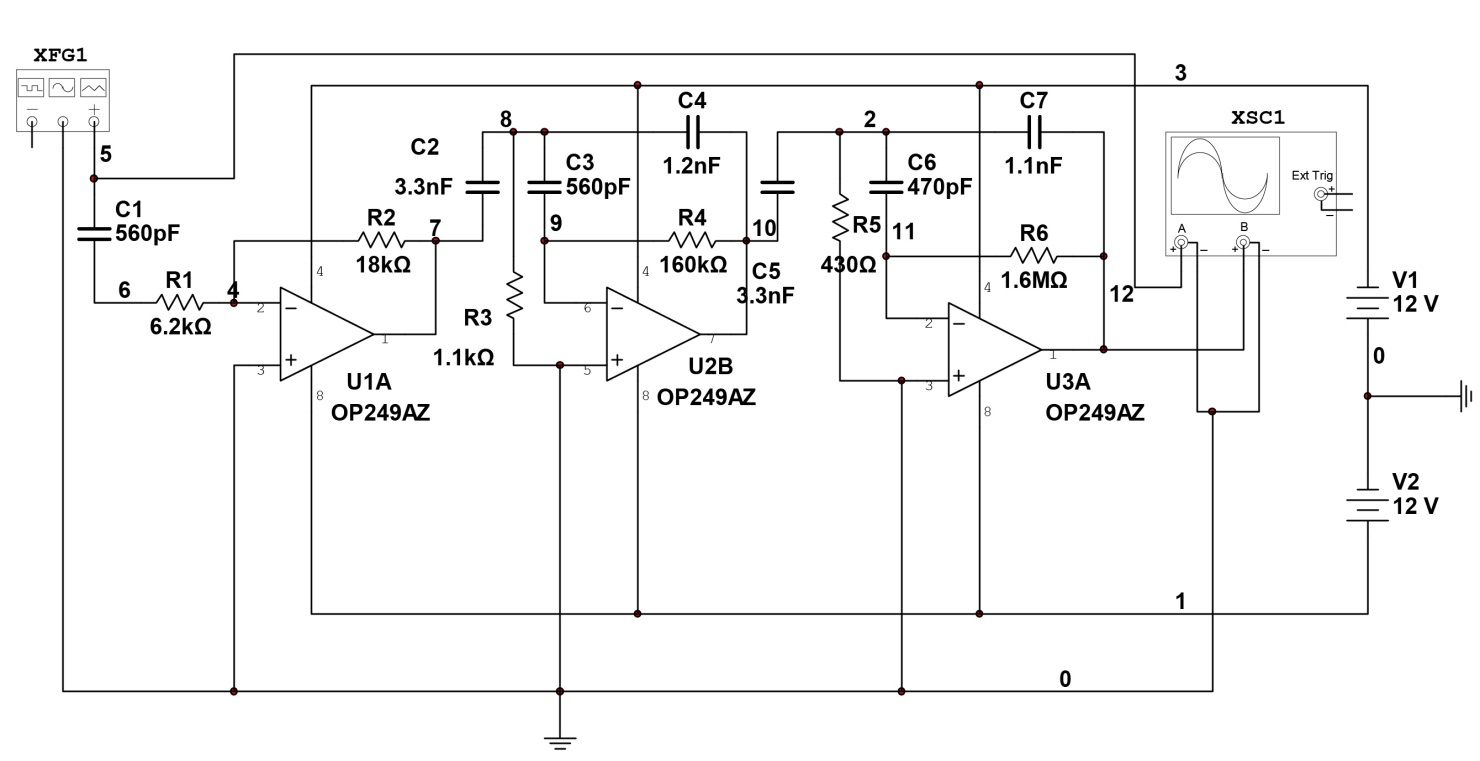 Рис.13.Схема измерения переходной характеристики фильтра в симуляторе MultiSim 10.  Рис.14. Вид переходной характеристики фильтра в симуляторе MultiSim 10.  Рис.15. Реакция фильтра на треугольный сигнал частотой 20 кГц.   Заключение. В работе был спроектирован активный фильтр высоких частот 5-го порядка. Теоретически были рассчитаны переходные характеристики и построены графики АЧХ звеньев фильтра, рассчитаны и выбраны параметры элементов фильтра. Окончательно, была получена переходная характеристика всего фильтра и построены графики его АЧХ и ФЧХ. Для проверки теоретического расчёта схема фильтра была промоделирована в среде схемотехнического моделирования MultiSim 10. Сравнение результатов расчёта и результатов моделирования показало их хорошее совпадение. В процессе выполнения работы были получены ценные навыки и знания, которые, несомненно, пригодятся в практической работе по специальности. Список литературы. Л.1. Проектирование активных фильтров. Методические указания к курсовому проекту по дисциплине «Электроника и схемотехника».- Вологда, ВоГТУ, 2012.- 31 с.Л2. Л2. Хьюлсман Л. П., Аллен Ф. Е. Введение в теорию и расчет активных фильтров: Пер. с а н г л .— М.: Радио и связь, 1984.— 384 с., ил. Л3. Джонсон Д. и др. Справочник по активным фильтрам: Пер. с англ./' Д. Джонсон, Дж. Джонсон, Г. Мур. — М.: Энерго атомиздат, 1983. — 128 с., ил. Л.4. Активные RС-фильтры на операционных усилителях. Перевод с английского В. В. Масленникова и В. А. Меркуловой под редакцией Г, Н. Алексакова. «Энергия», 1974 год. Л5.ТитцеУ. Шенк К. Полупроводниковая схемотехника. Справочное руководство. Пер.с нем.-М, Мир,1982.-512 с., ил. |
