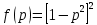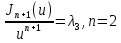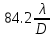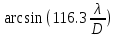СВЧ. Курсовой проект по дисциплине Антенны и устройства свч
 Скачать 1.72 Mb. Скачать 1.72 Mb.
|
|
Казанский национальный исследовательский технический университет им. А.Н. Туполева Институт радиоэлектроники и телекоммуникаций Кафедра радиоэлектронных и телекоммуникационных систем Курсовой проект по дисциплине «Антенны и устройства СВЧ» Тема проекта: «Антенна с устройством контроля мощности СВЧ» Выполнил студент группы 5202 Павлов В.П. Руководитель доцент кафедры РТС Стахова Н.Е. Казань 2012 Содержание Введение ……………………………………………….………….…4 Расчет характеристик антенны………………………………….….6 Расчет параметров облучателя………………………….………...15 Расчет профиля зеркала……………………………..……………..19 Технология изготовления зеркала…………………………..….…21 Заключение………………………………………..………..……….22 Список литературы…………………………………………………23 . Приложение: Графическая часть ВВЕДЕНИЕ Зеркальные антенны применяют в различных диапазонах волн: от оптического до коротковолнового, особенно широко в сантиметровом и дециметровом диапазонах. Эти антенны отличаются конструктивной простотой, возможностью получения различных ДН, хорошими диапазонными свойствами и др. Существуют различные типы зеркальных антенн: параболические зеркала (параболоид, усеченный параболоид и параболический цилиндр), сферические зеркала, плоские и уголковые зеркала, а также зеркальные антенны специальной формы, двух- и многозеркальные антенны, зеркально-рупорные антенны. Зеркальная параболическая антенна состоит из металлической поверхности, выполненной в виде параболоида вращения и небольшой слабонаправленной антенны – облучателя, установленной в фокусе параболоида и облучающий внутреннюю поверхность последнего. В двухзеркальной антенне используются две отражающие поверхности: основная – большое параболическое зеркало и вспомогательная – малое зеркало в виде гиперболоида (антенна Кассегрена) или эллипсоида вращения (антенна Грегори). В антенне Кассегрена роль малого зеркала состоит в переотражении падающей на него сферической волны облучателя на большое зеркало. При этом вследствие геометрических свойств гиперболы отражаемая малым зеркалом сферическая волна как бы исходит из первого фокуса, совмещаемого с фокусом большого зеркала. Эта волна трансформируется большим зеркалом в плоскую. Параболическое зеркало излучает так, как будто в его фокусе находится мнимый облучатель, создающий сферическую волну. Второй фокус малого зеркала совмещается с фазовым центром облучателя. К достоинствам двухзеркальной системы можно отнести то, что она является более компактной, чем однозеркальная, и обеспечивает более равномерное распределение возбуждения по раскрыву, а также является более помехозащищенной. А недостатки – затенение раскрыва малым зеркалом и элементами его крепления, переливание энергии облучателя через края этого зеркала (это, тем не менее, не так опасно как для однозеркальной антенны, так как вызывает только рост УБЛ), а также реакция малого зеркала на облучатель и связанное с этим ухудшение диапазонных свойств. В приближении геометрической оптики двух зеркальная антенна может быть сведена к эквивалентной однозеркальной параболической антенне, имеющей такое же распределения поля в раскрыве и такие же направленные свойства – с учетом затенения малым зеркалом. Расчет направленных свойств осуществляется с использованием параметров облучателя и эквивалентного параболоида. РАСЧЕТ ХОРАКТЕРИСТИК АНТЕННЫ. Двухзеркальная антенна Кассегрена состоит из облучателя, параболического зеркала или рефлектора и небольшого гиперболического зеркала – субрефлектора. Принцип действия антенны Кассегрена заключается в том, что сферическая волна облучателя преобразуется с помощью последовательного отражения от двух зеркал в плоскую волну в фокальной плоскости рефлектора (апертуре), где и формируется синфазное амплитудное распределение. В основных схемах двухзеркальных антенне (Кассегрена и Грегори), а также в их модификациях улучшение амплитудного распределения достигается не только выбором диаграммы направленности (ДН) облучателя и фокусного расстояния зеркала (как в однозеркальных параболических антеннах), но и подбором параметров субрефлектора и коррекцией его профиля совместно с профилем основного зеркала (рефлектора). Для расчета антенны используются следующие данные: f = 1…2 ГГц, 2ʘE = 2ʘH УБЛ = -28дБ, КСВ ≤ 1.3, Характеристики устройства контроля мощности: Переходное ослабление -20дБ, КСВ≤1.1 Условия эксплуатации – земная станция космической связи. Исходя из заданной частоты, определим длину волны по следующей формуле:  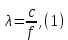 где c – скорость света с = 3·108 м/с, f – заданная частота сигнала. 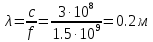 Для рабочей частоты длина волны составит λ=0.2м. Пользуясь заданным уровнем КСВ, можно найти КПД антенны по формуле: 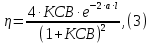 По условию КСВ ≤ 1.3, следовательно для расчета КПД выберем близкое максимальное значение КСВ = 1,3. Поскольку затухание в антенне очень мало и стремится к нулю, а так же длина линий передачи имеет очень малое значение, пренебрежем экспоненциальным множителем. Конечная формула КПД: 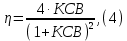 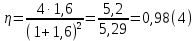 Далее вычисленные КПД и коэффициент усиления будет использоваться, для нахождения непосредственно КНД антенны. 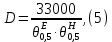 где  – ширина ДН на уровне 0,5 по мощности в плоскостях Е и Н. Исходя из равенства углов не трудно будет выразить ШДН в обоих плоскостях. – ширина ДН на уровне 0,5 по мощности в плоскостях Е и Н. Исходя из равенства углов не трудно будет выразить ШДН в обоих плоскостях.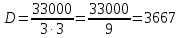 Пользуясь таблицами представленными в использованной литературе (Молочков) с амплитудными распределениями для круглых раскрывов выберем АР и функцию ее аппроксимации. При выборе руководствуемся известным нам параметром УБЛ = -28дБ. Используя данные из таблицы – основных характеристик волнового фронта и диаграмм направленности найдем диаметр раскрыва зеркала. Таблица №1
Из выбранного распределения стало возможно определить значение КИП=0,56, степень формулы распределения амплитуды n=2 и формулу для расчета диаметра зеркала. 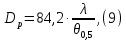 Исходя из формулы (9) выразим и рассчитаем диаметр большого зеркала Dp. 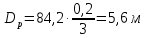 Для нахождения фокусного расстояния f-, используется оптимальное соотношение 0,3-0,5. При таком соотношении исключаются протекания противофазных токов в площади раскрыва зеркала. 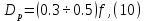 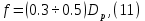 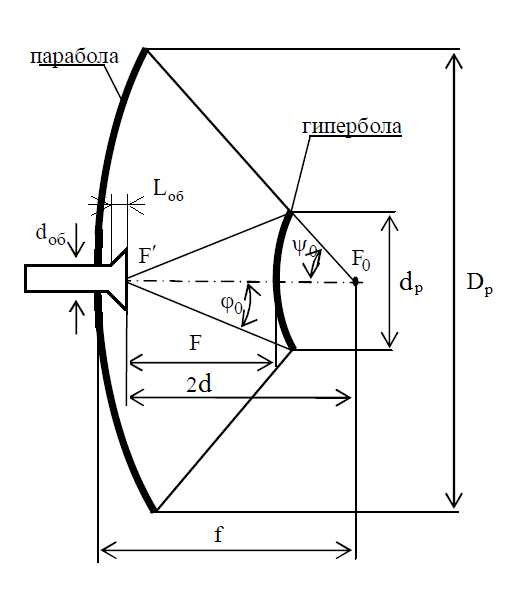 Рис. 2 – Двухзеркальная антенна Кассегрена. 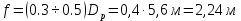 Вычисленные параметры составляют систему параболического рефлектора определяющего следующей формулой: 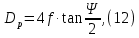 Из этого соотношения вычислим половину угла раскрыва зеркала ψ. 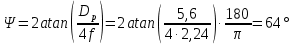 Далее расчет диаметра малого зеркала dpможно вычислить из соотношений приведенных ниже. Как следует из источника (В.И. Антюфеев, В.Н. Быков УДК 621.396.67) , с уменьшением эксцентриситета ( e→1 ) при постоянном угле ψ уменьшается диаметр субрефлектора и апертурный угол φ. При этом, для того чтобы субрефлектор перехватывал большую часть энергии облучателя, ДН последнего должна быть достаточно узкой, что достигается с помощью увеличения диаметра апертурного облучателя Dоб. При этом в случае Dоб > L происходит недопустимое затенение рефлектора. К тому же уменьшение диаметра субрефлектора при e→1 ограничено дифракционным пределом 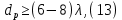 ниже которого отраженное от субрефлектора поле будет сильно искажаться из-за возрастания интенсивности краевых волн, подобных волнам, возникающим на кромках параболического рефлектора. Если же увеличивать эксцентриситет (например, e→3 ), то увеличивается и угол φ, что позволяет использовать слабонаправленные облучатели с меньшим диаметром Dоб . Однако при этом возникает опасность чрезмерного затенения апертуры субрефлектором из-за возрастания его диаметра. По этим причинам величину эксцентриситета выбирают в пределах 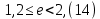 Эксцентриситет определим равным e = 2. Перечисленные параметры и вычисленный диаметр параболического рефлектора Dp связаны следующими выражениями: 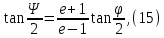 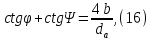 Исходя из формулы (15) определим значение апертурного угла φ. 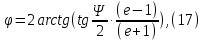 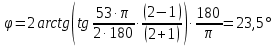 Расчет диаметра субрефлектора dp производится по формуле, полученной из выражения (16) с учетом (15) и (12): 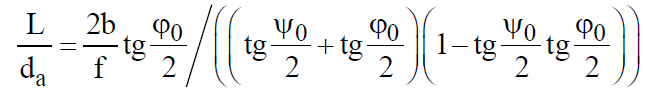 , (18) , (18)Анализ зависимости dp / Dp от ψ, φ при различных значениях 2b/ f , показывает, что при 2b = f , когда облучатель расположен в вершине параболического рефлектора, субрефлектор имеет предельные значения диаметра, что приводит к недопустимому затенению рефлектора. Так, при 2b/ f ≈ 1 и величине угла φ = 30, в диапазоне углов ψ = 50 – 80 значение диаметра субрефлектора находится в пределах dp = (0,375 - 0,312) Dp . Уменьшение отношения 2b /f при постоянном φ снижает затенение апертуры рефлектора субрефлектором. В связи с этим значения данного параметра необходимо выбирать в пределах 0,35 ≤ 2b /f ≤ 0,7. Исходя из вышеперечисленного, для уменьшения затенения апертуры выберем отношение 2b /f равным 0,7 и рассчитаем диаметр малого зеркала. 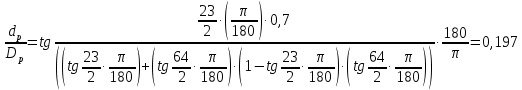 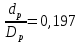 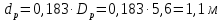 Зная угол раскрыва и диаметр малого зеркала, воспользовавшись гиперболическим соотношением взятым из литературы Молочкова (19) рассчитаем фокусное расстояние малого зеркала: 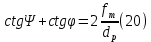 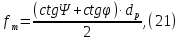 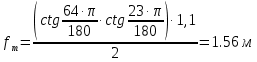 Все необходимые механические данные найдены, за исключением расстояния Lоб на котором будет крепиться облучатель. Для этого воспользуемся ранее взятым соотношением 2b /f = 0,7 и зная фокусное расстояние вычислим Lоб. 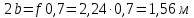  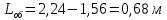 Диаграмму направленности ДН двухзеркальной антенны с большим зеркалом в виде параболоида вращения можно найти, рассматривая эквивалентную однозеркальную антенну. Если оставить большое зеркало без изменения, то следует найти диаграмму направленности виртуального облучателя. 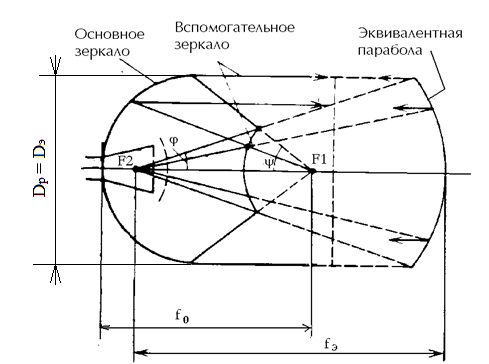 Рис. – 3 Эскиз эквивалентного параболического зеркала. Такое зеркало называют эквивалентным параболическим зеркалом (эквивалентной параболой). Фокусное расстояние fэ эквивалентного зеркала можно найти из соотношения: 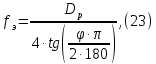 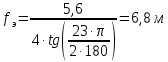 Далее нужно рассчитать ДН полученной антенны. Для расчета как наиболее просто необходимо использовать метод эквивалентного параболоида. Для расчета использовалась программа «Zercal.exe»  Рис. – 4 Ввод данных в программу Zercal.exe 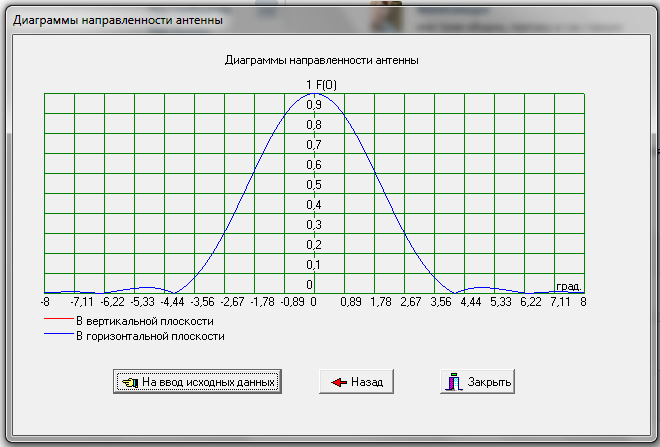 Рис. – 4 Диаграмма направленности антенны с УБЛ 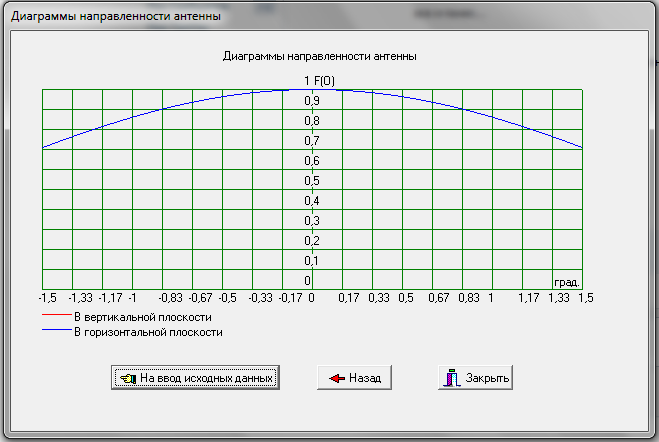 Рис. – 4 Ширина диаграммы направленности По диаграмме можно определить, что ШДН  3˚ значение совпадает с расчетными значениями формулы (7). 3˚ значение совпадает с расчетными значениями формулы (7).Из известного соотношения 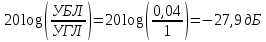 УБЛ соответствует заданному - 28  -27,9дБ -27,9дБРАСЧЕТ ПРОФИЛЯ ЗЕРКАЛА Параболический профиль зеркала обеспечивает одинаковые длины электрических путей от облучателя, установленного в фокусе параболоида вращения, до каждой точки плоскости раскрыва (свойство параболы). В декартовой системе координат парабола описывается уравнением:  где x и z полярные координаты, f – фокусное расстояние. В данном случае x изменяется от 0 до D/2 Данные для большого зеркала: f = 2.24м, Dp = 5.6м Проведя расчеты построим график параболы для большого зеркала: 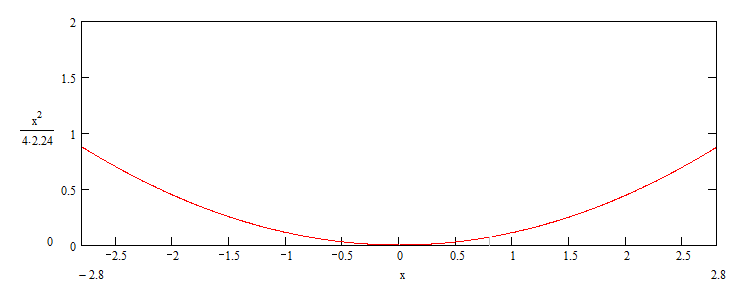 Рис.8 – График параболы большого зеркала Таблица для построения параболического зеркала (указана только одна половина)
Следует глубина большого зеркала составляет – 875 мм. Далее рассчитаем и построем график параболы для малого зеркала исходя из следующих данных: f = 1.1м, Dp = 1.56м 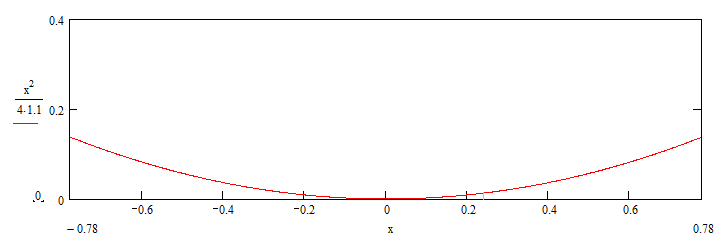 Рис.9 – График параболы большого зеркала Таблица для построения параболического зеркала (указана только одна половина)
Следует глубина большого зеркала составляет – 13,8 мм. РАСЧЕТ ПАРАМЕТРОВ ОБЛУЧАТЕЛЯ В качестве облучающего элемента в используется конический рупор, возбуждаемый волной Н11, которая подводится к нему с помощью круглого волновода. Т.к. облучатель работает непосредственно с малым зеркалом, его ширина ДН будет соответствовать углу раскрыва малого зеркала. В результате сможем вычислить КНД излучателя: 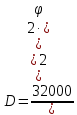 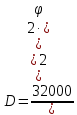 15,1 15,1Конические рупоры имеют оптимальные размеры, которые могут быть определены с помощью следующей таблицы: 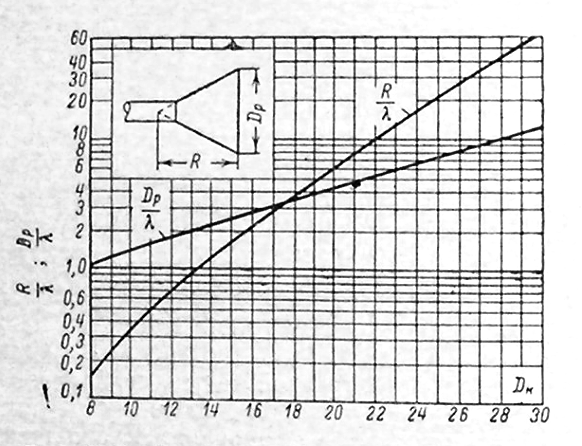 Рис. 5 – Зависимость размеров оптимальных конических рупоров в длинах волн от величины КНД. Имея КНД излучателя из соотношения и исходя соотношения Dи/λ которое равно 5, вычислим найдем диаметр раскрыва облучателя: 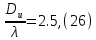 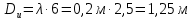 Длина оптимального рупора R, диаметр его раскрыва связаны Dи и длина волны связаны следующим отношением. 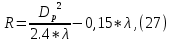 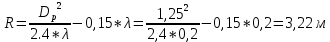 Основным типом волны в круглом волноводе является волна H11 c наибольшей критической длиной волны ( 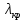 = 3,41a). Ближайшим высшим типом является волна E01( = 3,41a). Ближайшим высшим типом является волна E01(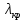 = 2,6a). Рабочий диапазон частот в определяется условием: = 2,6a). Рабочий диапазон частот в определяется условием: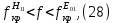 Далее, следует найти диаметр волновода через 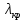 , для нашей частоты она лежит в пределах 2,61a< , для нашей частоты она лежит в пределах 2,61a< 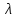 < 3,41a. < 3,41a. Т.к. длина волны 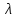 в волноводе имеет очень малое значение, то из предыдущего соотношения возьмем в волноводе имеет очень малое значение, то из предыдущего соотношения возьмем 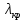 волны H11 с запасом т.е. волны H11 с запасом т.е. 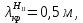 исходя из этого рассчитаем радиус волновода: исходя из этого рассчитаем радиус волновода: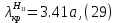 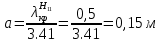 Определим максимальную мощность, которая может быть передана через волновод: 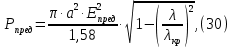 Т.к. место эксплуатации антенны аэродром, то 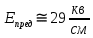 – для воздуха при нормальном атмосферном давлении, нормальной ионизации, нормальной температуре. Из-за возможных неоднородностей, качества поверхности внутренних стенок волновода, чистоты заполняющего волновод воздуха большее значение – для воздуха при нормальном атмосферном давлении, нормальной ионизации, нормальной температуре. Из-за возможных неоднородностей, качества поверхности внутренних стенок волновода, чистоты заполняющего волновод воздуха большее значение 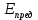 брать не рекомендуется. Все данные указывать в сантиметрах: брать не рекомендуется. Все данные указывать в сантиметрах: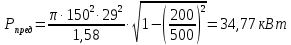 Максимальная мощность удовлетворяет условиям задания P=70Вт. Для того, чтобы организовать вывод приемного сигнала, для дальнейшей его обработки необходимо реализовать согласование с коаксиальным кабелем. Для этого нам потребуются различные переходы. Переход от прямоугольного волновода с волной Н10к круглому волноводу с волной Н11,осуществляется путем постепенной деформации поперечного сечения волновода от прямоугольного к круглому. 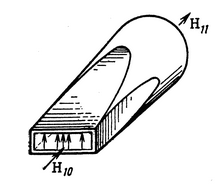 Рис. 6 Переходы от прямоугольного волновода к круглому. Если длина перехода составляет примерно длину волны в волноводе или больше ее, то его полоса пропускания равна полосе частот круглого волновода с волной типа Н11. Размеры волноводов выбираются такими, чтобы в них в заданном диапазоне частот могли распространяться только низшие типы волн, соответственно Н10 в прямоугольном и Н11— в круглом волноводе. Если длина такого перехода превышает длину волны, то отражения в широкой полосе частот оказываются незначительными. 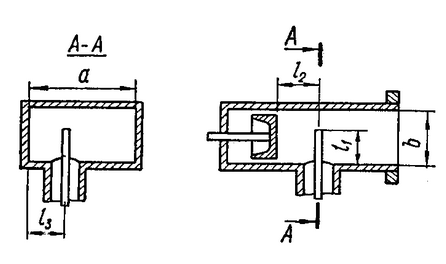 Рис. 7 – Волноводно-коаксиальный переход. Соединение коаксиальной линии с прямоугольным волноводом является трансформатором волны типа Т в коаксиальной линии в волны типа Нили Ев прямоугольном волноводе и относится к числу так называемых зондовых переходов. Для возбуждения волны типа Нв волновод вводится штырь (зонд), перпендикулярный продольной оси волновода (рис. 11а), т. е. поперек волновода. Штырь, являющийся продолжением внутреннего проводника коаксиальной линии, служит антенной, излучающей электромагнитную энергию в волновод или отбирающей ее из волновода. Для получения минимального отражения волн от перехода, необходимо коаксиальную линию и волновод согласовать, т. е. создать режим бегущих волн. Согласование осуществляется подбором длины штыря l1,расстояния l2 от штыря до заглушки (поршня), замыкающей накоротко волновод, и расстояния l3 от штыря до ближайшей узкой стенки волновода. Для согласования перехода в диапазоне частот используется подвижный короткозамыкающий поршень, компенсирующий реактивную составляющую входного сопротивления штыря. РАСЧЕТ УСТРОЙСТВА КОНТРОЛЯ МОЩНОСТИ  Главная часть устройства контроля мощности являются - два направленных ответвителя. Волноводный мост со многими отверстиями связи состоит из двух прямоугольных волноводов, связанных множеством отверстий в общей узкой стенке (Рис.4.1). Требуется прямое затухание 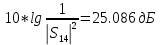 . .Если считать, что КБВ нагрузки в плече 2 составляет 0.909, то для получения эффективной направленности 30дБ собственную направленность ответвителя согласно графику на рис. 4.2 следует иметь Dc=70дБ, т.е. Dc=107. 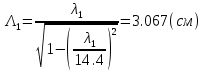 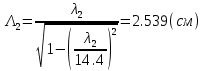 откуда масштабный коэффициент 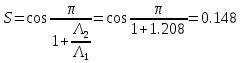 Число звеньев 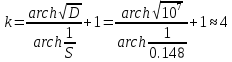 По таблице 11.11 [4-стр.598-601] для k=4 и S=0.148 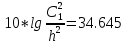 дБ дБ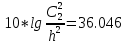 дБ дБи уточненное значение требуемой собственной направленности Dc составляет Dc = 71.97 дБ. Так как 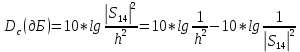 , ,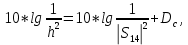 т.е.  Искомые затухания звеньев согласно 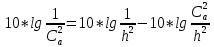 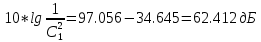 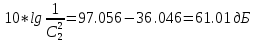 П  ричем 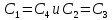 . .Рис.4.3. Эквивалентная схема одного отверстия связи. Из эквивалентной схемы отверстия (рис.4.3) следует формула для его затухания 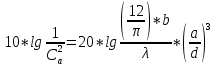 , ,следовательно d1=0.938мм и d2=0.945мм. ТЕХНОЛОГИЯ ИЗГОТОВЛЕНИЯ Технология изготовления параболических антенн в первую очередь зависит от диаметра D и количества изготовляемых изделий. При серийном изготовлении антенн небольшого размера, а также антенн с вынесенным облучателем применяется литье под давлением из полимерных пластмасс с применением соответствующих форм и с последующей металлизацией зеркальной поверхности. Параболические отражатели средних размеров изготавливаются штамповкой из соответствующих круглых заготовок. Складывающиеся антенные системы имеет смысл самостоятельно изготавливать лишь для работы в нижней части микроволнового диапазона, так как на более высоких частотах они не смогут удовлетворить поставленным требованиям по точности выполнения зеркальной поверхности. Обработку зеркальной поверхности по контуру можно выполнить на программируемом карусельном станке. Это самый быстрый и элегантный способ. Можно для этого использовать и шаблоны. Особое внимание нужно уделять системе крепления облучателя. Она должна позволять точно совместить фазовый центр облучателя, который располагается где-то вблизи его апертуры, с фокусом параболического зеркала. Для центрирования облучателя на оси параболического отражателя используются совершенно одинаковые растяжки системы крепления облучателя; они должны закрепляться на зеркале на строго одинаковых расстояниях от оси и его вершины. Условием стабильного приема высокого качества является жесткость полной антенной системы и жесткая фиксация направления ее главного излучения (даже в условиях воздействия ветра). Металлизированное покрытие зеркала окрашивается матовой светопоглощаюшей краской (полимерная краска), которая одновременно со светопоглощением выполняет и защитные функции. Фокусирование в антенной системе солнечного излучения, падающего на антенну с направления приема, может вызвать искажения в работе приемной головки. ЗАКЛЮЧЕНИЕ В ходе курсового работы была спроектирована двухзеркальная параболическая антенна по схеме Кассегрена и произведены основные расчеты параметров, характеризующих работу антенны и построены диаграммы направленности всей антенны. В процессе проектирования удалось реализовать антенно-фидерное устройство удовлетворяющее исходным данным курсового проекта, а именно обеспечить работу двухзеркальной антенны по схеме Кассегрена на частоте 1…2 ГГц с шириной ДН в 3 градуса с уровнем боковых лепестков не более –27,9 дБ и коэффициентом использования поверхности КИП равным 0,56. Все основные данные по сборке имеются в чертежах в приложении. Так же в ходе курсового проектирования был лучше изучен и закреплен материал курса СВЧ устройства и антенны и получен ценный практический опыт по расчёту основных параметров двухзеркальной антенны по схеме Кассегрена. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Жук М. С., Молочков Ю. Б. Проектирование линзовых, сканирующих, широкодиапазонных антенн и фидерных устройств. – М.: Энергия, 1973. Власов В.И., Берман Я. И. Проектирование высокочастотных узлов радиолокационных станций. – Ленинград 1961 В.И. Антюфеев, В.Н. Быков, Т.Д. Бережная, А.М. Гричанюк, В.А. Краюшкин, МЕТОДИКА РАСЧЕТА ХАРАКТЕРИСТИК ДВУХЗЕРКАЛЬНОЙ АНТЕННЫ Зузенко В. А., Кислов А. Г., Цыган Н. Я. Расчет и проектирование антенн. – Л.: ЛВИКА, 1969. |