Курсовой проект по дисциплине Железобетонные и каменные конструкции
 Скачать 1.59 Mb. Скачать 1.59 Mb.
|
2.4 Расчет продольного ребра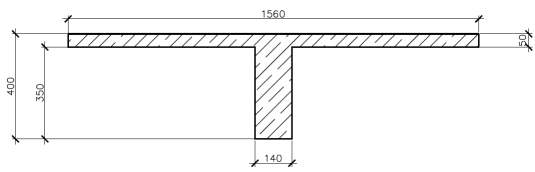 Рисунок 11 – Поперечное сечение продольного ребра Таблица 9 – Нагрузки на 1 м ребристой плиты
С учетом коэффициента надежности по классу ответственности здания: Для расчетов по I группе предельных состояний: 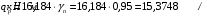 ; ;Для расчета по II группе предельных состояний: полная: 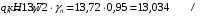 ; ;длительная: 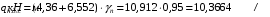 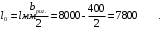 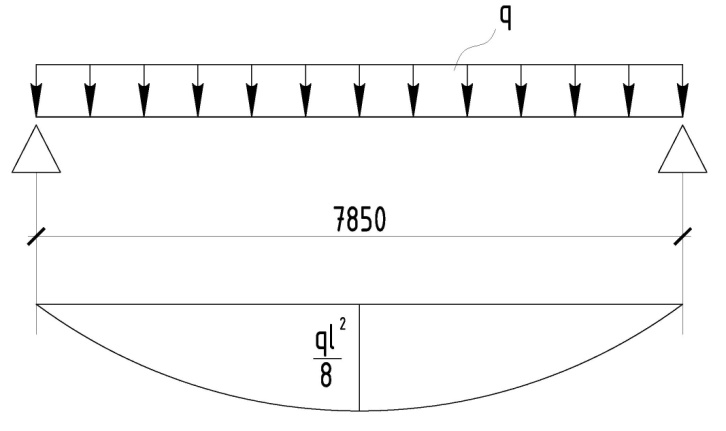 Рисунок 12 – Расчетная схема продольного ребра h0=400-30=370мм. Класс предварительно напрягаемой арматуры А-IV Rs=510 МПа Rs ser=590 МПа Расчетные усилия: Для расчетов по I группе предельных состояний: 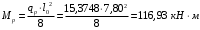 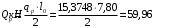 Для расчетов по II группе предельных состояний: 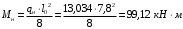 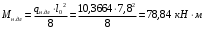 Назначаем эффективную максимальную величину предварительного напряжения арматуры: 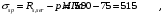 где p – (при электротермическом способе натяжения арматуры) определяется по формуле  Проверяю условие (1) п. 1,23 /1/  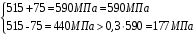 Предварительное напряжение при благоприятном влиянии с учетом точности натяжения арматуры будет равно:  , , где  согласно п. 1.27 /1/. согласно п. 1.27 /1/.Определяем положение нейтральной оси 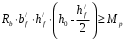 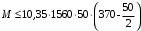 116,93·106 Н·мм < 278,52·106 Н·мм Так как условие выполняется, то граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной 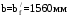 . .Определяем коэффициент статического момента αm 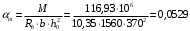 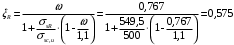  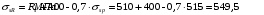 Проверяем условие ξ=0,0544<ξR=0,575; ζ=0,9728.Условие выполняется.  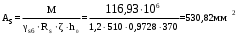 Принимаем арматуру - 2 стержня Ø20 А-IV, Аs= 628 мм2 Расчет плиты по I группе предельных состояний Расчет прочности сечений, наклонных к продольной оси. Из условия свариваемости принимаем поперечные стержни диаметром 5 мм класса Вр-I с числом каркасов – 2 с шагом поперечных стержней s=150 мм согласно требованиям /1/ п. 5.27. Аsw = 19,6∙2=39,2 мм2 Rsw = 260 МПа Rbt = 0,9∙0,9=0,81 МПа Еs=170000 МПа Еb=27000 МПа Проверяем условие  где φw1 – коэффициент учитывающий влияние хомутов, нормальных к продольной оси элемента 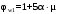 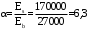 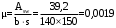  Коэффициент φb1 вычисляется по формуле  Коэффициент β = 0,01, для тяжелого бетона  тогда: 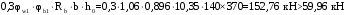 Условие выполняется, прочность по наклонной полосе между трещинами обеспечена. Проверяем условие:  ; ;где, коэффициент φb3 согласно пункту 3.31 /1/ для тяжелого бетона принимаем равным 0,6. Коэффициент φn, учитывающий влияние продольных сил равен 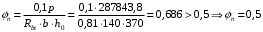 где 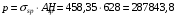 Коэффициент φb3 по /1/ п 3.31 для тяжелого бетона принимаем равным 0,6. тогда: 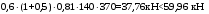 Условие не выполняется необходимо поперечное армирование. Определяю длину проекции наиболее опасного наклонного сечения на продольную ось элемента: 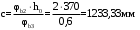 Коэффициент φb2, учитывающий влияние вида бетона, принимаем для тяжелого бетона равным 2,0. Коэффициент, φf, учитывающий влияние сжатых полок в тавровых и двутавровых элементах равен: 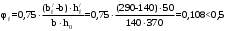   Поперечное усилие, воспринимаемое бетоном:  Усилие в хомутах на единицу длины элемента равняется: 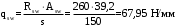 . .Определяем длину проекции наиболее опасной наклонной трещины на продольную ось элемента: 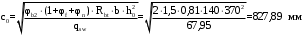 ; ;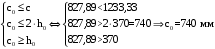 Проверяем условие: 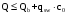 ; ; . .Условие выполняется, следовательно, прочность наклонного сечения обеспечена. 2.5 Расчет ребристой плиты по предельным состояниям II группы Согласно табл. 2 /1/ ребристая плита, эксплуатируемая в закрытом помещении и армированная напрягаемой арматурой класса A-IV должна удовлетворять 3-й категории требований по трещиностойкости, т.е. допускается непродолжительное раскрытие трещин шириной 0,4 мм и продолжительное – 0,3 мм. Прогиб плиты от действия постоянных и длительных нагрузок не должен превышать предельного значения – 2,5 см по табл.4 /1/. Определение геометрических характеристик приведенного сечения плиты 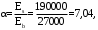 площадь приведенного сечения определяется по формуле  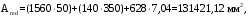 статический момент площади приведенного сечения относительно нижней грани определяется по формуле   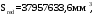 расстояние от нижней грани до центра тяжести приведенного сечения определяется по формуле  момент инерции приведенного сечения определяется по формуле    момент сопротивления приведенного сечения по нижней зоне определяется по формуле  момент сопротивления приведенного сечения по верхней зоне определяется по формуле  упругопластичный момент сопротивления по растянутой зоне определяется по формуле 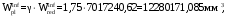 где γ = 1,75 – для таврового сечения с полкой в сжатой зоне упруго пластичный момент сопротивления по растянутой зоне в стадии изготовления и обжатия элемента определяется по формуле 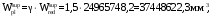 где γ = 1,5 – для таврового сечения с полкой в растянутой зоне при   |