Курсовой проект по дисциплине Железобетонные и каменные конструкции
 Скачать 1.59 Mb. Скачать 1.59 Mb.
|
2.8 Расчет по раскрытию трещин.Плечо внутренней пары сил при непродолжительном действии полной нагрузки вычисляется по формуле: 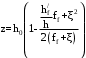 при: 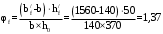 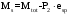 , так как усилие обжатия приложено в центре тяжести напрягаемой арматуры esp=0, тогда , так как усилие обжатия приложено в центре тяжести напрягаемой арматуры esp=0, тогда 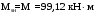 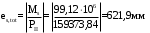 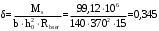 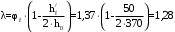 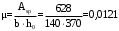 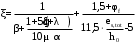 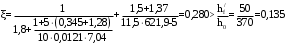 Плечо внутренней пары сил равно: 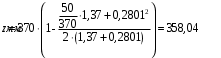 Плечо внутренней пары сил при непродолжительном действии постоянной и длительной нагрузок 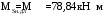 : :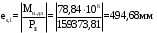 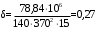 λ = 1,28; μ = 0,0121 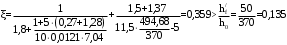 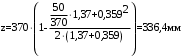 Расчет по раскрытию трещин, нормальных к продольной оси плиты Приращение напряжений в растянутой арматуре от непродолжительного действия полной нагрузки определяем по формуле 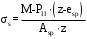 где M = Mн = 99,12 кНм; z – расстояние от центра тяжести площади сечения арматуры до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной; esp = 0, т. к. усилие обжатия приложено в центре тяжести напрягаемой арматуры 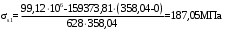 Приращение напряжений в растянутой арматуре от непродолжительного действия постоянной и длительной нагрузки M = Mн.дл = 78,84 кНм 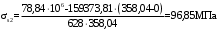 Приращение напряжений в растянутой арматуре от продолжительного действия постоянной и длительной нагрузки 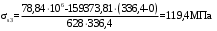 Ширину раскрытия трещин от непродолжительного действия полной нагрузки определяем по формуле 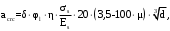 где δ – коэффициент, принимаемый для изгибаемых элементов равным 1; φl – коэффициент, принимаемый равным 1; η – коэффициент, принимаемый при стержневой арматуре периодического профиля равным 1; σ – напряжение в стержнях крайнего ряда арматуры или приращение напряжений от действия внешней нагрузки; μ – коэффициент армирования сечения; d – диаметр арматуры. 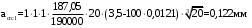 Ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузки 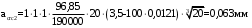 Ширина раскрытия трещин от продолжительного действия постоянной и длительной нагрузки 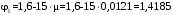 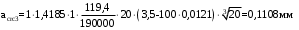 Ширина непродолжительного раскрытия трещин: 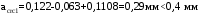 Ширина продолжительного раскрытия трещин: 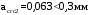 Требования к плите по трещиностойкости удовлетворяются. 2.9 Расчет прогиба плитыРасчет выполняется с учетом раскрытия трещин согласно п. 4.27 /1/ от действия постоянной и длительной нагрузок. M = Mн = 99,12 кН∙м; Nн = PII = 159,37 кН На участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых элементов определяется по формуле 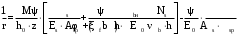 где M – момент относительно оси, нормальной к плоскости действия момента и проходящий через центр тяжести площади сечения арматуры, от всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, и от усилия предварительного обжатия; z – расстояние от центра тяжести площади сечения арматуры до точки приложения равнодействующих усилий в сжатой зоне сечения над трещиной; ψs – коэффициент, учитывающий работу растянутого бетона на участке с трещинами; ψb – коэффициент, учитывающий неравномерность распределения деформаций крайнего сжатого волокна бетона по длине участка с трещинами; φf – 1,37; ξ – относительная высота сжатой зоны бетона; ν – коэффициент, характеризующий упругопластическое состояние бетона сжатой зоны; Nн – равнодействующая продольной силы и усилия предварительного обжатия. Полная кривизна для участка с трещинами в растянутой зоне определяется по формуле 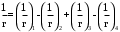 где: где: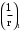 – кривизна от непродолжительного действия всей нагрузки; – кривизна от непродолжительного действия всей нагрузки;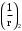 – кривизна от непродолжительного действия постоянных и длительных нагрузок; – кривизна от непродолжительного действия постоянных и длительных нагрузок; 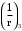 – кривизна от продолжительного действия постоянных и длительных нагрузок; – кривизна от продолжительного действия постоянных и длительных нагрузок; 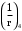 – кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия – кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатияКривизна от непродолжительного действия всей нагрузки: 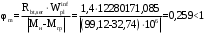 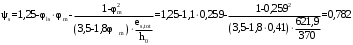 при 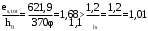 принимаем 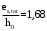 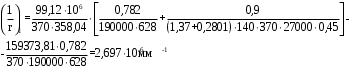 Кривизна от непродолжительного действия постоянных и длительных нагрузок: 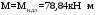 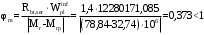  при при 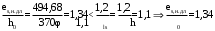 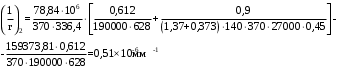 Кривизна от продолжительного действия постоянных и длительных нагрузок: 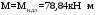 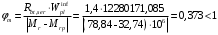  при при 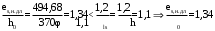 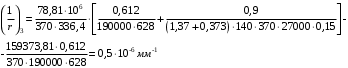 Кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия: Определяем относительные деформации бетона, вызванные его усадкой и ползучестью от усилия предварительного обжатия: 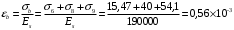 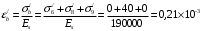 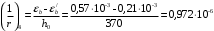 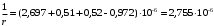 Вычисляем прогиб по формуле 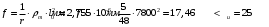 Вычисленное значение прогиба удовлетворяет требованиям. |
