электротехника. задача 1 готовая. 1 Краткие сведения по теории Стержень подвергается деформации кручения, когда в его поперечных
 Скачать 107.37 Kb.
|
|
1. КРУЧЕНИЕ 1.1. Краткие сведения по теории Стержень подвергается деформации кручения, когда в его поперечных сечениях возникают крутящие моменты. Их величина определяется методом сечений по участкам, границами которых являются места приложения внешних крутящих моментов, действующих на стержень. Из условия равновесия следует, что величина крутящего момента в поперечном сечении стержня численно равна алгебраической сумме внешних крутящих моментов, действующих по одну сторону от рассматриваемого сечения.  Рис. 1 Крутящий момент М К в поперечном сечении вала считается положи- тельным, когда внешний крутящий момент Т действует по часовой стрелке при взгляде на соответствующий торец вала (рис. 1). Эпюра крутящего момента – это график, показывающий изменение ве- личины внутреннего крутящего момента в поперечных сечениях вала в зависи- мости от координаты Х. Для цилиндрического стержня круглого поперечного сечения диаметром d величина касательного напряжения τ в точке поперечного сечения, находя- щейся на расстоянии ρ от центра (рис. 2), определяется по формуле: (1) где М К – величина крутящего момента в сечении, I Р – полярный момент инер- ции сечения. Для круглого сплошного сечения диаметром d полярный момент инерции I Р определяется по формуле: . (2) Максимальные касательные напряжения τ в поперечном сечении вала действуют в точках, наиболее удаленных от центра, т. е. при ρ=0,5·d (см. рис. 2). Их величина определяется по формуле: (3) где W Р – полярный момент сопротивления. Для круглого сплошного сечения W Р определяется по формуле: (4) Условие прочности при кручении имеет вид: задача № 1 К стальному валу приложены три известных момента Т 1 , Т 2 , Т 3 (рис. 1). Требуется: 1. Установить, при каком значении момента Х угол поворота правого концевого сечения вала равен нулю. 2. Для найденного значения Х построить эпюру крутящих моментов. 3. При заданном значении [τ] определить диаметр вала и округлить его значение до ближайшего, равного: 30, 32, 34, 35, 36, 38, 40, 42, 45, 47, 48, 50, 52, 53, 55, 56, 60, 62, 63, 65, 67, 70, 71, 72, 80, 85, 90, 95, 100 мм. 4. Построить эпюру углов закручивания. 5. Найти наибольший относительный угол закручивания. Исходные данные  Рис. 1 Таблица 1. Исходные данные к задаче
G = 0,4·E; Е = 2·10 11 Па. Решение. 1. Определение момента Х Применим принцип независимости действия сил. Определим угол поворота сечения под действием каждого момента, деформирующего вал на определенном участке, по отдельности. Результирующий угол поворота будет равен алгебраической сумме всех углов поворота от действия каждого момента с учетом знака. Допустим, что действует только момент Х на участке вала ЕА длиной: L ЕА = a + b + c + a = 1,6 + 1,4 + 1,6 + 1,6 = 6,2 м. Согласно рис. 1 знак момента Х будет отрицательным, а угол поворота сечения Е относительно неподвижной заделки в сечении А будет равен:  Допустим, что действует только момент Т 3 на участке вала DА длиной: L DА = c + b + a = 1,6 + 1,4 + 1,6 = 4,6 м. Тогда угол поворота сечения D относительно неподвижной заделки А равен:  Рассуждая аналогичным образом об остальных участках, получим следующие выражения: L CА = b + a = 1,4 + 1,6 = 3 м. 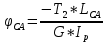 L BА = a = 1,6 = 1,6 м.  По условию задачи угол поворота  от действия всех крутящих моментов равен нулю, тогда: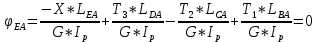 Откуда выразим искомый момент:   Так как значение момента Х получилось положительным, то его направление соответствует показанному направлению Х на расчетной схеме (см. рис.1); в противном случае направление следует поменять на обратное. 2. Построение эпюры крутящих моментов Не вычисляя по уравнениям равновесия значение реактивного момента в заделке и используя метод сечений, запишем выражения для крутящего момента по участкам вала. Будем двигаться при этом справа налево в сторону заделки, начиная со свободного конца и используя правило знаков согласно рис. 1. Границы первого участка: 0 ≤ х 1 ≤ а. М К1 =  = – Х = – 923 Нм = – 0,923 кНм.Границы второго участка: а ≤ х 2 ≤ а + c. М К2 = = – Х + Т 3 = –923 + 1600 = 677 Нм = 0,677 кНм.Границы третьего участка: а + c ≤ х 3 ≤ а + b + с. М К3 = = – Х + Т 3 – Т 2 = – 923 + 1600 –1400 = -723 Нм = -0,723 кНм.Границы четвертого участка: а + b + с ≤ х 4 ≤ а + b + с + а. М К4 = = – Х + Т 3 – Т 2 + Т 1 = – 923 + 1600 –1400 +1600 = 877 Нм = 0,877 кНм.Полученные значения откладываем в масштабе на каждом из соответствующих участков вала (рис. 2). После построения эпюры крутящих моментов делаем ее проверку, используя правило проверки правильности построения эпюры крутящих моментов: в тех сечениях вала, где приложены сосредоточенные крутящие моменты, на эпюре будут скачки на их величину в соответствии с направлением хода построения и выбранным правилом знаков. 3. Определение диаметра вала Так как сечение вала по длине не меняется, то по условию прочности оп- ределим минимальный диаметр вала круглого сплошного сечения:  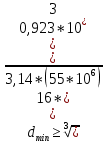 Полученное значение округлим до ближайшего большего, заданного по условию задачи, d = 45 мм 4. Построение эпюры углов закручивания Сначала определим величину полярного момента инерции ( I Р) при кручении вала круглого сплошного сечения. Так как сечение вала по длине постоянно, то для каждого участка имеем:   Выражения для углов закручивания на каждом участке вала получены в п. 1, поэтому определим теперь их численные значения, начиная с левого конца вала. Заделка неподвижна, поэтому угол закручивания сечения в ней φ А =0 рад. Угол поворота сечения В относительно неподвижной заделки А:  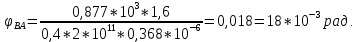 Угол поворота сечения С относительно неподвижной заделки А складывается из суммы углов поворотов сечения В относительно А и С относительно В, то есть     Тогда;  Аналогично определим углы закручивания сечений D и E относительно неподвижной заделки А;    Тогда ;     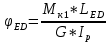 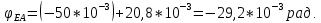Полученные значения углов закручивания сечений в соответствии с их знаками откладываем на эпюре в масштабе и соединяем их прямыми линиями (см. рис. 5). Тот факт, что угол поворота правого концевого сечения вала равен нулю, может служить проверкой проведенных вычислений. 5. Определение наибольшего относительного угла закручивания По эпюре углов закручивания видно (см. рис. 5), что наибольший угол закручивания по абсолютной величине равен φ MAX = 14,47·10 −3 рад на участке длиной a = 1,1 м, тогда величина наибольшего относительного угла закручивания (рад/м) будет равна  Рис. 2 | |||||||||||||||||||||||||||