не то что ты ищешь студент. Абдинаги. Сопротивление образованию трещин. Определение момента трещинообразования при неупругой работе бетона сжатой зоны

• Название: Сопротивление образованию трещин. Определение момента трещинообразования при неупругой работе бетона сжатой зоны
• Анкор: не то что ты ищешь студент
• Дата: 20.11.2022
• Размер: 312.03 Kb.
• Имя файла: Абдинаги.docx
• Тип: Реферат; #799974

Министерство образования и науки Республики Казахстан

Международная образовательная корпорация

Казахская головная архитектурно-строительная академия



РЕФЕРАТ

Тема: «Сопротивление образованию трещин. Определение момента трещинообразования при неупругой работе бетона сжатой зоны»

Выполнил:Әбдінағи Ж.Б.

Группа: РПЗС 20-11

Проверила: Ажгалиева Б.А.

Алматы 2022 г.

Трещиностойкость и перемещения железобетонных элементов

При работе под нагрузкой в железобетонных конструкциях могут возникать трещины, в процессе развития которых повышается деформативность элементов, создаются условия для коррозии арматуры, снижается долговечность. Под трещиностойкостью железобетонных конструкций понимают их сопротивление образованию и раскрытию трещин. В зависимости от условий эксплуатации и напряженного состояния трещины в железобетонных элементах не могут быть допущены, или их ширина раскрытия ограничивается предельно допустимой величиной.

Требования по отсутствию трещин предъявляются к конструкциям, у которых должны быть обеспечены непроницаемость либо повышенная долговечность. К таким конструкциям относятся конструкции, находящиеся под давлением жидкости или газов, испытывающие воздействие радиации, уникальные сооружения, эксплуатируемые при сильном воздействии агрессивной среды. В остальных случаях трещины в железобетонных конструкциях допускаются, и трещино- стойкость обеспечивается ограничением ширины раскрытия трещин.

Расчет по образованию трещин производят для проверки необходимости расчета по раскрытию трещин, а также для необходимости учета трещин при расчете по деформациям. Под непродолжительным раскрытием трещин следует понимать их раскрытие при совместном действии постоянных, длительных и кратковременных нагрузок, под продолжительным раскрытием — только от действия постоянных и длительных нагрузок, без учета кратковременных нагрузок.

Трещины в нормальных сечениях элемента не образуются, если соблюдается условие трещиностойкости:



где F — усилие в нормальном сечении элемента от нормативных внешних нагрузок (изгибающий момент, продольная сила);

F_crc — внешнее усилие, которое может воспринять сечение перед образованием трещин.

Расчет по образованию трещин, нормальных к продольной оси элемента. В основу расчета положены следующие предпосылки: сечения элемента плоские до деформации остаются плоскими после деформации; появление трещин в бетоне растянутой зоны происходит после того, как напряжения в крайнем растянутом волокне достигнут расчетных сопротивлений на растяжение  и предельных относительных деформаций бетона на растяжение  Напряжения в напрягаемой арматуре будут равны сумме предварительного напряжения (с учетом потерь и коэффициента точности натяжения) и приращения напряжений из-за деформаций растянутого бетона после погашения его обжатия; напряжения в ненапрягаемой арматуре предварительно напряженных элементов равны сумме сжимающих напряжений от усадки и ползучести бетона и приращения растягивающего напряжения из-за деформаций растянутого бетона.

Предельные относительные деформации растянутого бетона при двузначной эпюре деформаций в нормальном сечении для тяжелого бетона принимают  при однозначной равномерной эпюре деформаций (осевое растяжение) — 



Центрально-растянутые элементы. Расчет центрально-растянутых элементов производят в соответствии с условием (13.1):



где 

А_ь — площадь бетона поперечного сечения растянутого элемента;

Р — усилие предварительного обжатия бетона;

N — продольная сила от нормативных нагрузок.

При соблюдении условия (13.2) трещины в сечениях, нормальных к продольной оси, не образуются.

Изгибаемые, внецентренно сжатые и внецентренно растянутые элементы. Расчет возможно выполнять по трем моделям.

1-я модель. В общем случае расчет по образованию нормальных трещин производят с использованием деформационной модели сплошного сечения с учетом неупругих деформаций бетона. Эта модель включает уравнения равновесия, условие деформирования в виде плоского поворота и плоского перемещения сечения (гипотеза плоских сечений) и диаграмм деформирования о — г бетона и арматуры при сжатии и растяжении.

Критерием образования трещин при расчете на основе нелинейной деформационной модели является достижение относительных деформаций растянутого бетона s_bt от нагрузок своих предельных значений  т.е:



Такой расчет выполняется с применением специальных программ на ЭВМ.

2-я модель. Расчет производят по упрощенному методу. Считается, что в сжатой зоне бетон работает в упругой стадии, а в растянутой — в упругопластической. Работа растянутого бетона характеризуется диаграммой деформирования по типу диаграммы Прандтля. В этом случае эпюра напряжений в сжатой зоне нормального сечения имеет треугольную форму, а в растянутой зоне — трапециевидную с максимальными напряжениям, равными расчетным значениям сопротивления бетона растяжению  и с максимальными относительными деформациями  (рис. 13.1). Этот расчет заключается в проверке условия, что нормальные трещины в сечениях не образуются, если момент от внешних сил М_{ не превышает момента внутренних усилий перед образованием трещин М_сгс:



где — изгибающий момент внешних сил относительно нулевой линии.

Для изгибаемых элементов  здесь М — изгибающий момент

от действующей нагрузки (рис. 13.1а).

Для внецентренно сжатых и внецентренно растянутых элементов (рис 13.16) соответственно:



где е»₀, е₀ — эксцентриситеты продольной сжимающей и растягивающей сил относительно центра тяжести приведенного сечения; е₁ — расстояние от центра тяжести приведенного сечения до нулевой лини (см. рис. 13.1):



здесь у_с — расстояние от наиболее сжатого волокна бетона до центра тяжести приведенного поперечного сечения; х — высота сжатой зоны, определяется из условия равенства нулю проекций всех сил на горизонтальную ось (ZX = 0).

Допускается высоту сжатой зоны определять без учета площади арматуры. Тогда уравнение для определения высоты сжатой зоны имеет вид: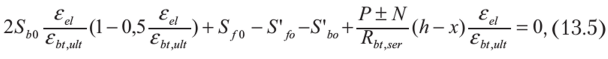



где S»_bo, S_bo — статические моменты площадей сечения бетона соответственно сжатой и растянутой зон ребра элементов таврового и двутаврового сечений относительно нулевой линии: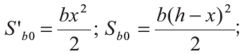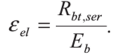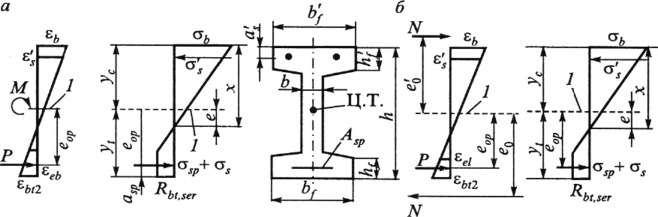



— статические моменты площадей свесов полок соответственно сжатых и растянутых относительно нулевой линии:



— относительная деформация растянутого бетона: 



Рис. 13.1. Схема напряженно-деформированного состояния сечения элемента при проверке образования трещин: при действии изгибающего момента (а) и продольной силы (б);

1 — уровень центра тяжести (ц.т.) приведенного поперечного сечения

Допускается принимать отношение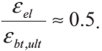 

Знак «+» в формуле (13.5) принимают при сжимающей силе N, знак « — » — при растягивающей.

В предварительно напряженных конструкциях высота сжатой зоны перед образованием трещин больше, чем в элементах без предварительного напряжения, она может составлять х = (0,7—0,9) h.

Расстояние от наиболее сжатого волокна до центра тяжести приведенного сечения определяется по формуле: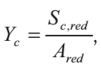



где  — статический момент приведенного поперечного сечения элемента

относительно наиболее сжатого волокна бетона, равный:



— площадь приведенного поперечного сечения, равная:



здесь А и S_c — соответственно площадь всего бетонного сечения и его статический момент относительно наиболее сжатого волокна бетона;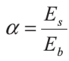

— площади поперечного сечения и их статические моменты относительно наиболее сжатого волокна соответственно растянутой и сжатой арматуры;

— коэффициент приведения арматуры к бетону.

Момент образования трещин определяют по формуле:



где W_x — момент сопротивления для крайнего растянутого волокна бетона, определяемый с учетом неупругих деформаций растянутого бетона; е_ор — эксцентриситет усилия предварительного обжатия бетона Р относительно центра тяжести приведенного сечения.

Момент сопротивления W_l определяют с учетом достижения крайним растянутым волокном бетона при образовании трещин предельной относительной деформации ?_{bt uit} по формуле (без учета арматуры):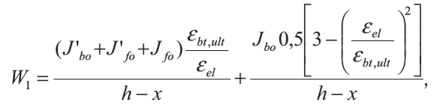



где  — моменты инерции площадей сечения бетона соответственно

сжатой и растянутой зон ребра таврового и двутаврового сечения относительно нулевой линии:



— моменты инерции площадей сечения свесов полок соответственно сжатых и растянутых относительно нулевой линии: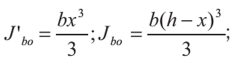 

3-я модель. В качестве первого приближения расчет железобетонных конструкций по образованию нормальных трещин возможно производить как для сплошного упругого тела. В этом случае критерием образования нормальных трещин является достижение напряжениями <5_bt в растянутом бетоне расчетных сопротивлений растяжению   Для обеспечения гарантий против образования нормальных трещин необходимо, чтобы соблюдалось условие (13.4).

Момент образования трещин определяют без учета неупругих деформаций растянутого бетона:



где 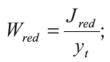 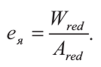— момент сопротивления сечения для крайнего растянутого волокна бетона:



— момент инерции приведенного поперечного сечения относительно его центра тяжести;

— расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется:



При внецентренном сжатии (растяжении) при проверке условия (13.4) момент внешних сил берется относительно ядровой точки, наиболее удаленной от растянутой зоны:

— при сжимающей силе;

— при растягивающей силе.

Момент образования трещин предварительно напряженных изгибаемых элементов в стадии эксплуатации возможно определять по способу ядровых моментов:



где W_pi — упругопластический момент сопротивления железобетонного сечения по растянутой зоне: 

у — коэффициент, учитывающий влияние нсупругих деформаций бетона растянутой зоны в зависимости от формы сечения; для прямоугольных и тавровых сечений с полкой в сжатой зоне 

Расчет по образованию трещин в упругой постановке дает более низкие результаты, чем расчет с учетом неупругих деформаций (2-я модель). С учетом этого обстоятельства может быть рекомендована следующая последовательность расчета по образованию трещин.

В начале производят расчет согласно 3-й модели (как наиболее простой и осторожной). Если этот расчет показывает, что трещины не образуются, тогда расчет по раскрытию трещин не производят, а расчет по деформациям производят как для сплошного упругого тела. Если этот расчет показывает, что трещины образуются, то производится расчет по раскрытию трещин и по деформациям с учетом трещин. При невыполнении требований по раскрытию трещин или по деформациям, производят более точный, но более сложный расчет по образованию трещин с учетом упругопластических деформаций растянутого бетона (2-я модель). Этот расчет может показать, что трещины не образуются, тогда расчет по раскрытию трещин не требуется, а расчет по деформациям производят как для сплошного тела.