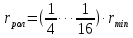Курсавая. Курсовая работа. Курсовой проект по дисциплине Механика 3
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
Примеры выполнения курсовой работыТема 1. Кинематическое исследование рычажного механизма 1.1. Исходные данные Дана схема (рис. 2), частота вращения ведущего звена nAB = 950 об/мин и длины звеньев rAB = 110 мм, lBC = 460 мм, lBD = 290 мм. Исследование механизма производится в 11-м положении (заданный угол поворота кривошипа). 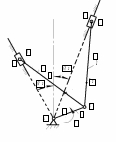 Рис. 2. Схема механизма 1.2. Описание построения плана механизма Принимаем длину кривошипа 1 на чертеже равной 40 мм. Расчет масштабного коэффициента производим по формуле
где 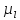 – масштабный коэффициент, м/мм; – масштабный коэффициент, м/мм;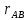 – длина кривошипа по заданию, м; – длина кривошипа по заданию, м;AB – длина кривошипа на чертеже, мм.  . .Расчет длин звеньев механизма на чертеже ведем, используя следующую формулу:
где 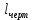 – длина звена на чертеже, мм; – длина звена на чертеже, мм;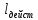 – действительная длина звена, м; – действительная длина звена, м;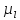 – масштабный коэффициент, м/мм. – масштабный коэффициент, м/мм.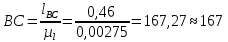 ; ;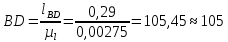 . .1.3. Структурный анализ механизма Составим описание звеньев и кинематических пар механизма и занесём их, соответственно, в табл. 1.1 и табл. 1.2. Таблица 1.1 Характеристика звеньев механизма
Таблица 1.2 Характеристика кинематических пар механизма
Степень свободы плоского механизма находится по формуле Чебышева
где 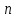 – число подвижных звеньев, в данном механизме их 5 (табл. 1.1); – число подвижных звеньев, в данном механизме их 5 (табл. 1.1);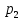 – число одноподвижных кинематических пар 5-го класса, в данном механизме их 7 (табл. 1.2); – число одноподвижных кинематических пар 5-го класса, в данном механизме их 7 (табл. 1.2);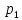 – количество двухподвижных пар 4-го класса, в данном механизме их нет (табл. 1.2). – количество двухподвижных пар 4-го класса, в данном механизме их нет (табл. 1.2).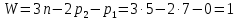 . .1.4. Построение кинематических диаграмм По найденным на планах механизма положениям ведомого звена 5 вычерчиваем график перемещения ползуна B, начиная от крайнего нижнего положения. Время оборота ведущего звена (кривошипа AВ) найдем по формуле
где 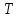 – время оборота кривошипа АВ, с; – время оборота кривошипа АВ, с;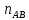 – частота вращения кривошипа АВ, об/мин. – частота вращения кривошипа АВ, об/мин.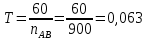 . .Изобразим это время на оси абсцисс отрезком x = 159 мм. Масштабный коэффициент времени на диаграмме рассчитывается по формуле
где 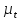 – масштабный коэффициент времени на диаграмме, с/мм; – масштабный коэффициент времени на диаграмме, с/мм;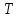 – время оборота кривошипа АВ, с; – время оборота кривошипа АВ, с;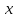 – принятая длина отрезка по оси абсцисс, мм. – принятая длина отрезка по оси абсцисс, мм.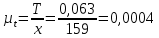 . .Масштаб перемещений на диаграмме, откладываемых по оси ординат, принимаем равным величине удвоенного масштаба длины на схеме механизма. 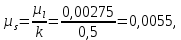 где 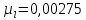 – масштабный коэффициент плана положений механизма, м/мм; – масштабный коэффициент плана положений механизма, м/мм;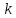 – коэффициент уменьшения (увеличения) диаграммы перемещений по сравнению с планом положений. – коэффициент уменьшения (увеличения) диаграммы перемещений по сравнению с планом положений.Масштабный коэффициент угла поворота кривошипа найдем по формуле
где 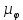 – масштабный коэффициент угла поворота кривошипа, рад/мм; – масштабный коэффициент угла поворота кривошипа, рад/мм;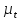 – масштабный коэффициент времени на диаграмме, м/мм; – масштабный коэффициент времени на диаграмме, м/мм;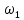 – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;Угловую скорость звена 1 можно найти по следующей формуле:
где 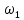 – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;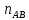 – частота вращения кривошипа АВ, об/мин. – частота вращения кривошипа АВ, об/мин.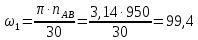 . .Тогда 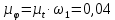 . .Дифференцируя график перемещений, получим график изменения скорости ведомого звена. Дифференцирование проводим графически методом хорд. Вычисляем масштабный коэффициент скорости на диаграмме
где  – масштабный коэффициент скорости на диаграмме, м · с-1/мм; – масштабный коэффициент скорости на диаграмме, м · с-1/мм;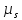 – масштабный коэффициент перемещений на диаграмме, м/мм; – масштабный коэффициент перемещений на диаграмме, м/мм;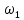 – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;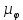 – масштабный коэффициент угла поворота кривошипа, рад/мм; – масштабный коэффициент угла поворота кривошипа, рад/мм;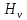 – полюсное расстояние, мм. – полюсное расстояние, мм.Полюсное расстояние 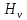 принимают равным 40 мм. принимают равным 40 мм.Тогда 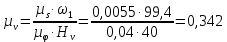 . .Аналогичным способом получим кривую ускорения, дифференцируя график скорости. Вычисляем масштабный коэффициент ускорения на диаграмме
где 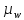 – масштабный коэффициент ускорения на диаграмме, м · с-2/мм; – масштабный коэффициент ускорения на диаграмме, м · с-2/мм; – масштабный коэффициент скорости на диаграмме, м · с-1/мм; – масштабный коэффициент скорости на диаграмме, м · с-1/мм;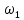 – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;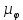 – масштабный коэффициент угла поворота кривошипа, рад/мм; – масштабный коэффициент угла поворота кривошипа, рад/мм;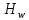 – полюсное расстояние, мм. – полюсное расстояние, мм.Полюсное расстояние 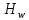 принимают равным 40 мм. принимают равным 40 мм.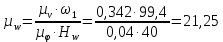 . .1.5. Описание построения плана скоростей От произвольно взятой точки Р отложим вектор скорости 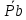 , который направлен перпендикулярно кривошипу в направлении , который направлен перпендикулярно кривошипу в направлении 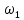 . Принимаем длину вектора . Принимаем длину вектора 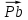 на плане скоростей равной 40 мм. на плане скоростей равной 40 мм.Вращение кривошипа задано схемой механизма и направлено против часовой стрелки. Скорость точки B кривошипа можно найти, предварительно рассчитав угловую скорость вращения кривошипа:
где 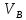 – скорость точки В кривошипа, м/с; – скорость точки В кривошипа, м/с;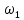 – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;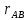 – длина кривошипа по заданию, м. – длина кривошипа по заданию, м.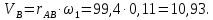 Расчет масштабного коэффициента скорости
где  – масштабный коэффициент скорости, м · с-1/мм; – масштабный коэффициент скорости, м · с-1/мм;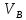 – скорость точки В кривошипа, м/с; – скорость точки В кривошипа, м/с;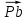 – длина вектора – длина вектора 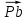 на плане скоростей, мм. на плане скоростей, мм.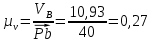 . .Для каждого из 12 положений: Скорость точки C ползуна найдем, решив совместно два векторных уравнения
Первое уравнение описывает движение точки С относительно точки В, а второе описывает движение точки С, принадлежащей ползуну. Скорость точки D ползуна найдем, решив совместно два векторных уравнения
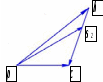
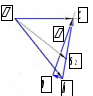
Первое уравнение описывает движение точки D относительно точки В, а второе описывает движение точки D, принадлежащей ползуну. Векторы скоростей 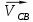 и и 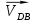 строим из точки B перпендикулярно шатунам 2 и 4 до их пересечения с осями xx и уу. строим из точки B перпендикулярно шатунам 2 и 4 до их пересечения с осями xx и уу.После построения плана скоростей определяем значения скоростей всех звеньев и точек механизма. Например: 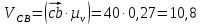 . .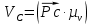 . .1.6. Описание построения плана ускорений От полюса π отложим вектор нормального ускорения в направлении от В к А в виде вектора 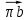 . .Нормальное (центростремительное) ускорение точки В кривошипа найдем по формуле
где 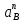 – нормальное ускорение точки В, м/с2; – нормальное ускорение точки В, м/с2;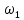 – угловая скорость звена 1, рад/с; – угловая скорость звена 1, рад/с;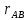 – длина кривошипа по заданию, м. – длина кривошипа по заданию, м.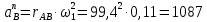 . .Принимаем длину вектора  . .Расчет масштабного коэффициента ускорения проведем по формуле
где 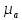 – масштабный коэффициент ускорения, м · с-2/мм; – масштабный коэффициент ускорения, м · с-2/мм;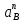 – нормальное ускорение точки В, м/с2; – нормальное ускорение точки В, м/с2;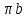 – длина вектора – длина вектора 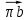 на плане скоростей, мм. на плане скоростей, мм.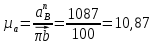 . .Для каждого из 2 положений: Ускорение точки C найдем, решив совместно два векторных уравнения
Ускорение точки D найдем, решив совместно два векторных уравнения
Нормальные ускорения 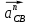 и и 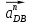 строим параллельно шатунам 2 и 4 соответственно, причем они направлены от точек С и D к точке В. строим параллельно шатунам 2 и 4 соответственно, причем они направлены от точек С и D к точке В.Тангенциальные ускорения 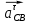 и и 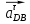 строим перпендикулярно нормальным ускорениям строим перпендикулярно нормальным ускорениям 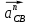 и и 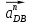 из конца векторов до пересечения с осями xx и yy. из конца векторов до пересечения с осями xx и yy.Для 0-го положения: Нормальное ускорение 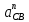 определим по формуле определим по формуле
где 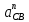 – нормальное ускорение звена CB, м/с2; – нормальное ускорение звена CB, м/с2; – длина вектора – длина вектора  скорости шатуна СВ на чертеже, мм; скорости шатуна СВ на чертеже, мм;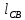 – действительная длина шатуна CB, м. – действительная длина шатуна CB, м.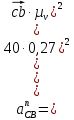 . .На плане ускорений длина вектора 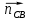 будет равна будет равна
где 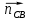 – длина вектора нормального ускорения точки B кривошипа, мм; – длина вектора нормального ускорения точки B кривошипа, мм;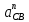 – нормальное ускорение звена CB, м/с2; – нормальное ускорение звена CB, м/с2;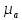 – масштабный коэффициент ускорения, м · с-2/мм. – масштабный коэффициент ускорения, м · с-2/мм.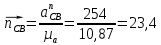 . .Нормальное ускорение 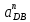 найдем по формуле (1.18) найдем по формуле (1.18)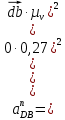 . .А длину вектора 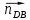 по формуле (1.19) по формуле (1.19)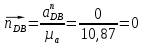 . .Для 11-го положения: Нормальное ускорение 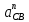 определим по формуле (1.18) определим по формуле (1.18)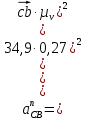 . .На плане ускорений длина вектора 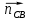 будет равна (1.19) будет равна (1.19)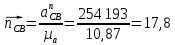 . .Нормальное ускорение 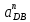 найдем по формуле (1.18) найдем по формуле (1.18)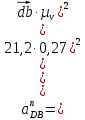 . .А длину вектора 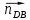 по формуле (1.19) по формуле (1.19)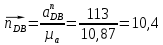 . .Тангенциальное ускорение звена СВ находим из плана ускорений по формуле
где  – тангенциальное ускорение звена CB, м/с2; – тангенциальное ускорение звена CB, м/с2;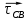 – величина вектора τСВ на плане ускорений; – величина вектора τСВ на плане ускорений;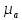 – масштабный коэффициент ускорения, м · с-2/мм. – масштабный коэффициент ускорения, м · с-2/мм.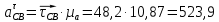 ; ;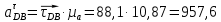 . .Сравнительный анализ Рассчитаем скорость и ускорение выходного звена, полученные построением планов скоростей. Для этого умножаем длину вектора абсолютной скорости ползуна С на масштабный коэффициент плана скоростей и длину вектора абсолютного ускорения на масштабный коэффициент плана ускорений.
Рассчитаем скорость и ускорение выходного звена, полученные построением диаграммы скоростей. Для этого умножаем ординату диаграммы скорости ползуна С на масштабный коэффициент диаграммы скоростей и ординату диаграммы ускорения на масштабный коэффициент диаграммы ускорений (например, для второго положения механизма).
Сравним полученные значения. Таблица 1.3 Сравнительный анализ скоростей и ускорений
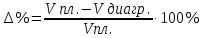 . .Тема 2. Синтез кулачкового механизма 2.1. Исходные данные и схема механизма Дана схема кулачкового механизма (рис. 3), угол удаления φу = 100º, угол дальнего стояния φд = 80º, угол возврата φв = 100º, минимальный угол передачи движения γmin= 60º и подъем толкателя h= 35 мм = 0,035 м. Направление вращения кулачка против часовой стрелки. 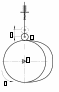 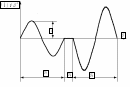 Рис. 3. Схема кулачкового механизма 2.2. Построение диаграммы 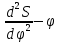 На оси абсцисс φ откладываем углы φУ, φД, φВв масштабе 2º/1 мм. Масштабный коэффициент угла поворота найдем по формуле
где 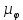 – масштабный коэффициент, рад/мм; – масштабный коэффициент, рад/мм;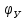 – угол удаления, рад.; – угол удаления, рад.;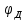 – угол дальнего стояния, рад.; – угол дальнего стояния, рад.;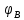 – угол возврата, рад.; – угол возврата, рад.;L– длина отрезка на чертеже, мм. 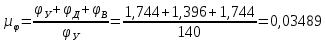 . .Длину отрезка ОР находим по формуле
где OP – длина отрезка OP на чертеже, мм; 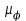 – масштабный коэффициент, рад/мм. – масштабный коэффициент, рад/мм.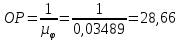 . .Высоту кривой принимаем равной 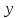 = 70 мм. = 70 мм.Разбиваем угол удаления и угол возврата на диаграмме на 12 равных частей. Масштабный коэффициент 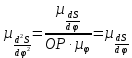 . .2.3. Построение диаграммы 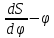 . .Диаграмма 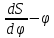 получается графическим интегрированием диаграммы аналогов ускорений получается графическим интегрированием диаграммы аналогов ускорений  . Для этого: . Для этого:– разбиваем угол удаления на 12 равных частей 01; 12; 23; ...; – из середины каждой части проведем перпендикуляр до пересечения с кривой 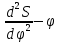 ;соединим полюс P с проекциями середин частей кривой на ось ;соединим полюс P с проекциями середин частей кривой на ось 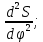 – на диаграмме 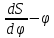 откладываем отрезки, параллельные соответствующим отрезкам, полученным в предыдущем подпункте. откладываем отрезки, параллельные соответствующим отрезкам, полученным в предыдущем подпункте.Все построения ведем в масштабном коэффициенте 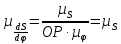 . .2.4. Построение диаграммы 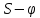 Диаграмму 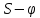 построим, графически проинтегрировав диаграмму аналогов скоростей построим, графически проинтегрировав диаграмму аналогов скоростей 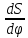 аналогично пункту 2.3. аналогично пункту 2.3.Замеряем наибольшую величину 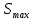 на чертеже, на чертеже, 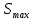 = 35,06 мм. = 35,06 мм.Масштабный коэффициент 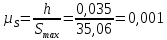 м/мм. м/мм.2.5. Определение минимального радиуса кулачка Берем на плоскости произвольную точку О, откладываем от неё отрезок ОА, равный ходу h толкателя. Этот отрезок размечаем в соответствии с диаграммой 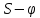 . Через точки деления проводим перпендикуляры к линии ОА. От точек деления на перпендикулярах откладываем влево при подъеме и вправо при опускании толкателя отрезки, взятые из графика . Через точки деления проводим перпендикуляры к линии ОА. От точек деления на перпендикулярах откладываем влево при подъеме и вправо при опускании толкателя отрезки, взятые из графика 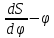 . Эти отрезки нужно откладывать в том масштабе, в котором отложен отрезок ОА, т. е. в масштабе . Эти отрезки нужно откладывать в том масштабе, в котором отложен отрезок ОА, т. е. в масштабе 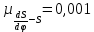 м/мм. Соединяем плавной кривой концы этих отрезков и получаем кривую м/мм. Соединяем плавной кривой концы этих отрезков и получаем кривую 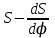 . Проводим под углом . Проводим под углом 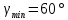 горизонтали две касательные к построенной кривой. Эти прямые образуют в итоге область, в которой может располагаться центр кулачка. Выбираем длину отрезка BО, равной горизонтали две касательные к построенной кривой. Эти прямые образуют в итоге область, в которой может располагаться центр кулачка. Выбираем длину отрезка BО, равной  = 60 мм на чертеже. Следовательно, минимальный теоретический радиус кулачка будет равен = 60 мм на чертеже. Следовательно, минимальный теоретический радиус кулачка будет равен
где 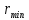 – минимальный теоретический радиус кулачка, м; – минимальный теоретический радиус кулачка, м; – масштабный коэффициент, м/мм; – масштабный коэффициент, м/мм;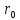 – минимальный радиус кулачка на чертеже, мм. – минимальный радиус кулачка на чертеже, мм.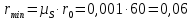 . .2.6. Профилирование кулачка Построения ведем в масштабе 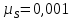 м/мм. Проведём окружность радиусом BA, полученным в предыдущем пункте. В произвольном месте окружности ОВ0 выберем точку отсчета В0. Соединим точку В0 с точкой О. От полученного луча в направлении (–ω) отложим угол φу, получим точку В12. Дугу В0В12 разделим на 12 равных частей (получим точки В1, В2, В3, …). Откладываем окружности, соответствующие перемещению толкателя в каждом из положений. Отмечаем точки пересечения отрезков ОВ0, ОВ1, ОВ2,… с соответствующими окружностями. Полученные точки соединяют плавной кривой – это теоретический профиль кулачка. Радиус ролика следует выбирать в диапазоне м/мм. Проведём окружность радиусом BA, полученным в предыдущем пункте. В произвольном месте окружности ОВ0 выберем точку отсчета В0. Соединим точку В0 с точкой О. От полученного луча в направлении (–ω) отложим угол φу, получим точку В12. Дугу В0В12 разделим на 12 равных частей (получим точки В1, В2, В3, …). Откладываем окружности, соответствующие перемещению толкателя в каждом из положений. Отмечаем точки пересечения отрезков ОВ0, ОВ1, ОВ2,… с соответствующими окружностями. Полученные точки соединяют плавной кривой – это теоретический профиль кулачка. Радиус ролика следует выбирать в диапазоне
где 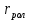 – радиус ролика толкателя, м; – радиус ролика толкателя, м;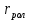 – принятый минимальный теоретический радиус кулачка, м. – принятый минимальный теоретический радиус кулачка, м.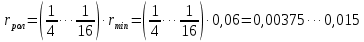 . .Принимают радиус ролика равным 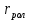 = 15 мм = 0,015 м. Тогда радиус ролика на чертеже будет равен (2.5) = 15 мм = 0,015 м. Тогда радиус ролика на чертеже будет равен (2.5)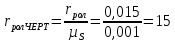 . .Далее радиусом ролика проводят дуги вовнутрь и строят огибающую линию теоретического профиля. Это и есть действительный профиль кулачка. |

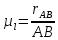
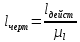 ,
, ,
,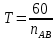 ,
,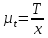
 ,
,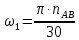 ,
,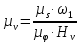
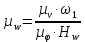 ,
,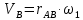 ,
,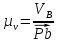 ,
,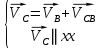 .
.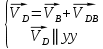 .
.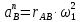
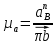
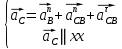 .
.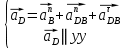 .
.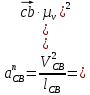 ,
,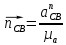 ,
,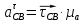 ,
,
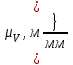
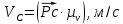
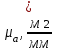
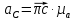

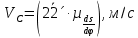


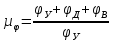 ,
,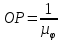 ,
,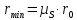 ,
,