курсовой. Курсовой проект по дисциплине здания, сооружения и их устойчивость при пожаре

• Название: Курсовой проект по дисциплине здания, сооружения и их устойчивость при пожаре
• Дата: 20.07.2022
• Размер: 1.68 Mb.
• Имя файла: курсовой.docx
• Тип: Курсовой проект; #633975
• страница: 5 из 6

3. РАСЧЕТ ФАКТИЧЕСКОГО ПРЕДЕЛА ОГНЕСТОЙКОСТИ ДЕРЕВЯННОЙ БАЛКИ ПОКРЫТИЯ

Фактический предел огнестойкости балки определяют по минимальному значению (Пф), вычисленному из следующих трех расчетных условий:

Первое условие - потеря прочности по нормальным напряжениям;

Второе условие - потеря прочности по касательным напряжениям;

Третье условие - потеря устойчивости плоской формы (деформирования) изгибаемых конструкций, находящихся в условиях пожара, зависит не только от глубины обугливания (Z) древесины, но также и от возможного выхода из строя нагельных соединений элементов связей.

3.1 Расчет по условию потери прочности по нормальным напряжениям

Определять требования к балке по огнестойкости будем расчетным методом с учетом действующей на балку нормативной нагрузки.

Нормативная нагрузка на 1 погонный метр длины балки: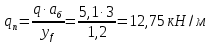



где q-полная расчетная нагрузка на балку, кПа (исходные данные, таблица4)

а_б -шаг балок, м (исходные данные, таблица 4)

y_f -усредненное значение коэффициента надежности по нагрузке=1,2

Изгибающий момент от действия нормативной нагрузки в сечении балки, находящемся на расстоянии l_рс: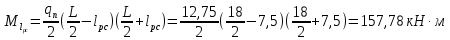



где q_n-нормативная нагрузка на 1 погонный метр длины балки, кН/м

L-расчетный пролет, м (исходные данные, таблица 4), м

Поперечная сила от нормативной нагрузки: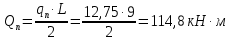

3.2 Расчет по условию потери прочности по касательным напряжениям

От действия силы Q_n в опорных сечениях конструкции возникают максимальные касательные напряжения.

Коэффициент изменения прочности по нормальным напряжениям: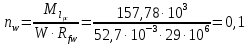



где W – момент сопротивления для прямоугольного сечения, равный: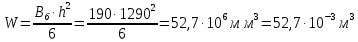



(h-высота балки, B_б-ширина балки: по исходным данным)

R_fw – расчетное сопротивление древесины изгибу при нагреве, равное 29 МПа (приложение1 таблица 2 [5]) для 1 сорта древесины.

Определим критическую глубину обугливания, при достижении которой наступает предельное состояние конструкции по огнестойкости (_n = R_fw), при действии нормальных напряжений.

По монограмме (приложение 2 рисунок 8.2. [5]) для числа обогреваемых сторон 4:

h / В_б = 1290/190 =7 и _w = 0,1 определяем, что: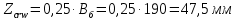



Коэффициент изменения прочности по касательным напряжениям: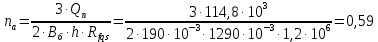



где R_fqs – расчетное сопротивление древесины скалыванию по приложение1 таблица 2 [5], равное 1,2 МПа (для 1 сорта древесины).

Определим критическую глубину обугливания, при достижении которой наступает предельное состояние конструкции по огнестойкости (_n = R_fqs), при действии касательных напряжений.

По монограмме (приложение 2 рисунок 8.2 [5]) для числа обогреваемых сторон 4:

h / В_б =1290/190 =7 и _а =0,59 определяем, что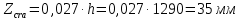



Из двух значений, z_crw и z_crа, выбираем наименьшее, таким образом z_cr =35,0 мм.

Определим время при пожаре от начала воспламенения древесины до наступления предельного состояния конструкции по огнестойкости: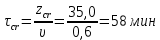



где  - скорость обугливания древесины, равная для сечения 1290х190 мм и клееной древесины 0,6 мм/мин (приложение 1 таблица 1 [5])

Фактический предел огнестойкости балки составляют:

Пф = _зо + _cr = 4 + 58 = 62 мин = 1,1 ч.

где _зо – время задержки обугливания, то есть время при пожаре от начала воздействия температуры на древесину до ее воспламенения, равное 4 мин.

3.3 Расчет по условию потери прочности плоской фермы

Потеря устойчивости плоской формы (деформирования) изгибаемых конструкций, находящихся в условиях пожара, зависит не только от глубины обугливания древесины, но также и от возможного выхода из строя нагельных соединений элементов связи.

Поскольку на заданной части длины (l_рс) время утраты несущей способности стальных креплений связей τ_рс = 15 мин. (0,25 ч.), то за это время значение глубины обугливания поперечного сечения балки с учетом того, что время задержки обугливания (τ₃₀ = 4 мин.) можно определить, исходя из соотношения: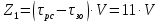



Для определения критического значения глубины обугливания, из условий сохранения устойчивости плоской формы (деформирования), необходимо:

1. 
   В пределах граничных значений (Z₁ = 11∙0,6 = 6,6 мм) и (Zi = 0,25∙B_б = 47,5 мм) произвольно выбрать не менее трех значений глубины обугливания:
   

Z₂ = 10 мм; Z₃ = 20 мм; Z₄ = 30 мм.

2. 
   Определить параметры (h/B_б = 7) и (Z_i/h):
   

Z₁/h = 6,6/1290 = 0,005

Z₂/h = 10/1290 = 0,0077

Z₃/h = 20/1290 = 0,016

Z₄/h = 30/1290 = 0,023

Z₅/h = 47,5/1290 = 0,037

3. 
   Определить по графикам значения коэффициентов η_wi: (приложение 2 рисунок 8.2 [5])
   

η_w1=0,90; η_w2=0,87; η_w3=0,75; η_w4=0,58; η_w5=0,42.

4. 
   Определить значение коэффициентов (φ_fmi) с учетом изменения размеров поперечного сечения в середине пролета балки в результате обугливания древесины с четырёх сторон по формуле: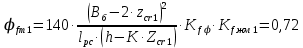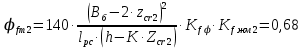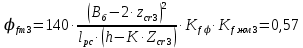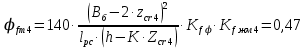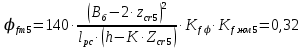
   

где К_fф – коэффициент, зависящий от формы эпюры изгибающих моментов на участке (l_рс).

Определяется по формуле: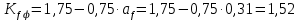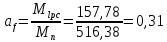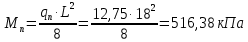







К=2 (количество сторон балки по высоте ее сечения, подвергающихся обугливанию: при трехстороннем обогреве К=1, четырехстороннем К=2)

K_fжмi – коэффициент, значение которого для односкатной балки приравнивается K=1;

5. 
   Вычислить величины напряжений в балке от внешней нагрузки, изменяющихся с уменьшением размеров поперечного сечения балки в результате ее обугливания на различную глубину: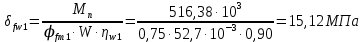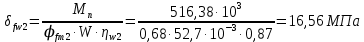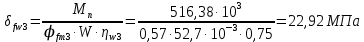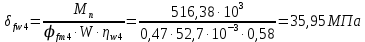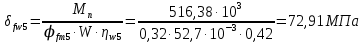
   

6. 
   Построить график зависимости напряжения от глубины обугливания при значении напряжения, равном (σ_fw = R_fw), определить критическую глубину обугливания.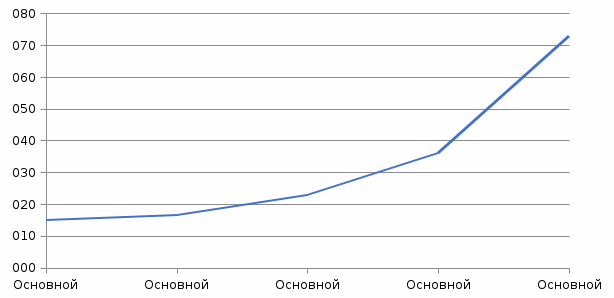
   

График 3.3.1 – Зависимости напряжения от глубины обугливания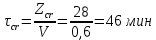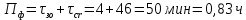





Вывод: Фактический предел огнестойкости балки принимают минимальное значение (П_ф), которое наступает по третьму условию потеря устойчивости плоской формы. П_ф=50 минут.