_ЖБК2 КП. Курсовой проект по учебному курсу Железобетонные и каменные конструкции 2 Вариант 1С, 2Д, 3т студент

• Название: Курсовой проект по учебному курсу Железобетонные и каменные конструкции 2 Вариант 1С, 2Д, 3т студент
• Дата: 14.12.2021
• Размер: 0.79 Mb.
• Имя файла: _ЖБК2 КП.docx
• Тип: Курсовой проект; #303092
• страница: 6 из 8

3.3 Расчет прочности ригеля по сечениям, нормальным продольной оси

Материалы:

Арматура: для рабочей арматуры (продольная) класс А400. Параметры: R_s (или расчетное сопротивление) составляет 355 МПа, E_s (или модуль упругости) составляет 200000 МПа.

Бетон: класс бетона В20, тяжелый бетон. Параметры: R_b (или расчетное сопротивление на сжатие) составляет 11,5 МПа; R_bt (или расчетное сопротивление на растяжение) составляет 0,9 МПа; E_b (или начальные модуль упругости) составляет 27500 МПа.
3.3.1 Проверка высоты сечения ригеля
Вычисляют рабочую высоту сечения: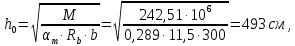



где α_m= ξ(1 – 0,5ξ) = 0,35(1 – 0,5 ∙ 0,35) = 0,289.

Окончательно принимаем высоту ригеля кратной 100 мм h = 700 мм.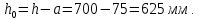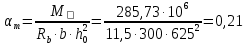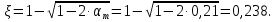







Сжатая зона: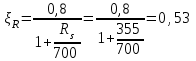

Площадь: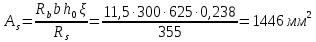



Отсюда принимаем 2 Ø 25 с A_s= 982 мм² и 2 Ø 18 с A_s = 509 мм² , площадь A_s= 1491 мм².

Сечение на крайней опоре

М_(12),1 = 70,85 кН∙ м, h₀ = h– a= 700 – 64 = 636 мм.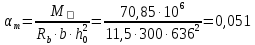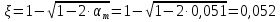





Площадь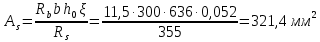



Принимаем 2Ø16 с A_s= 402 мм²

Сечение второй опоры М_(23),1 = 242,51 кН∙м.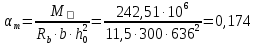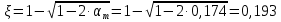





Площадь арматуры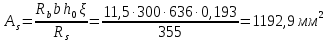



Принимаем 3Ø25 с A_s= 1473 мм²

Средний пролет М_l2 = 240,65 кН∙м, h₀ = h– a= 700 – 60 = 640 мм.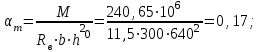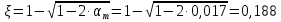





Площадь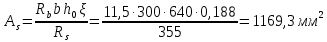



Принимаем 4 Ø 20 с A_s= 1256 мм²

Момент М = –32,61 кН∙м.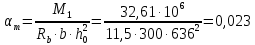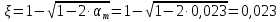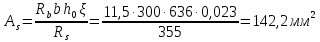







Приинимаем 2Ø10 с A_s= 157 мм².

3.3.2 Определение прочности ригеля

Прочность

Q_23max = 366,77 кН

Поперечная сила:

Q = Q_max – q ∙h_col /2 = 366,77 – 113,11∙0,4/2 = 344,15 кН;

Q_max = 344,15 < 0,3R_bbh₀ = 0,3∙11,5∙300∙546 = 558900 H = 558,9 кН,

Принимаем диаметр поперечных стержней 10 мм А400 с R_sw= 285 МПа.

Высота сечения h₀ = 636 мм.

Шаг стержня:

s_w = h₀ /2 = 636/2 = 318 мм и не более 300 мм.

При шаге s_w= 180 мм A_s= 78,5 мм². получаем A_sw= 2∙78,5 = 157 мм².

Силы Q₁₂ = 308,87 кН по схеме 1+2, Q₂₁ = 366,77 кН силе на грани опоры Q = 366,77 кН.

Расчет интенсивности хомута: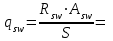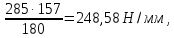

,

Проверяем условие обеспечения прочности сечения

q_sw>0,25R_btb = 0,25∙0,9∙300 = 67,5 Н/мм.

M_b= 1,5R_bt bh₀² = 1,5∙0,9∙300∙636² = 163,82∙10⁶ Н∙мм.

Так как q_sw/R_bt b = 248,58/ 0,9∙300 = 0,92 < 2, значение с определяем по формуле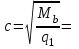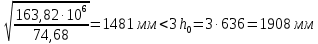



Откуда q₁ = q – 0,5q_v= 113,11– 0,5·76,86 = 74,68 кН/м

Согласно с₀ = 2h₀ = 2·636 = 1272 мм < с. Тогда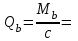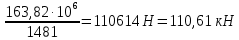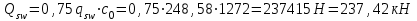





Q = Q_max – q₁c = 366,77 – 74,68·1,481 = 256,17 кН;

Q_b+ Q_sw= 110,61 + 237,42 = 348,03 > Q = 256,17 кН.

Согласно требованиям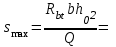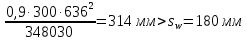

.

В средней части ригеля принимаем шаг поперечных стержней s_w2 = 400 мм < 0,75h₀.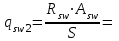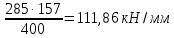



Проверяем условие q_sw2 ≥ 0,25R_btcb = 0,25·0,9·300 = 67,5 Н/мм, условие выполняется.

q_sw= 0,75(q_sw1 – q_sw2) = 0,75(248,58 – 111,86) = 102,54 Н/мм > q₁ = 74,68 Н/мм,

значение l₁ вычислим, приняв Q_b,min = 0,5R_bt bh₀ = 0,5·0,9·300·636 = 85860 Н;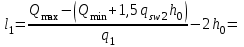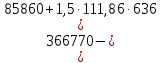



Принимаем длину участка с шагом хомутов s_w1 = 180 мм, равной 1,08 м.