_ЖБК2 КП. Курсовой проект по учебному курсу Железобетонные и каменные конструкции 2 Вариант 1С, 2Д, 3т студент

• Название: Курсовой проект по учебному курсу Железобетонные и каменные конструкции 2 Вариант 1С, 2Д, 3т студент
• Дата: 14.12.2021
• Размер: 0.79 Mb.
• Имя файла: _ЖБК2 КП.docx
• Тип: Курсовой проект; #303092
• страница: 5 из 8

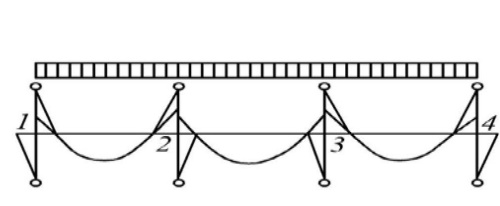
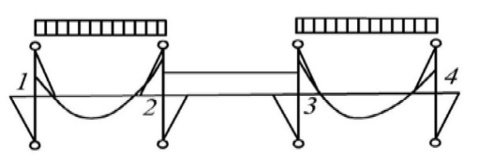
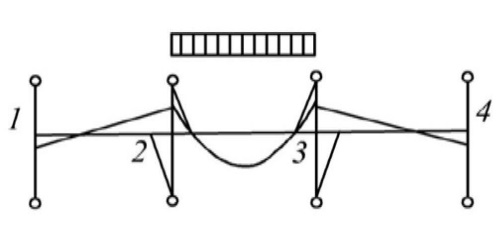
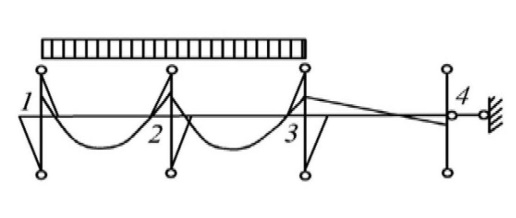
3. Проектирование ригеля

3.1 Расчетная схема и нагрузки
В курсовом проекте рассчитываем ригель среднего яруса.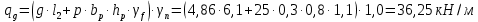



Временная нагрузка с учётом коэффициента по ответственности здания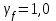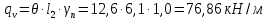



Расчётная полная нагрузка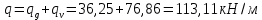

3.2 Расчет изгибающих моментов в сечениях ригеля

Жесткости колонны и ригеля: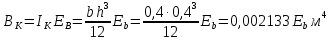





Коэф. к равен:



Расчетный пролет:



Результаты вычисления изгибающих моментов представлены в табл. 2.

№ п/п	Схема загружения	Опорные моменты, кНм
		М12	М21	М23	М32
1		-0,027 ∙36,25∙5,952= = - 34,65	-0,100 ∙36,25∙5,952= = -128,33	-0,091 ∙36,25∙5,952= = -116,78	-0,091 ∙36,25∙5,952= = -116,78
2		-0,036 ∙76,86∙5,952= = -97,96	-0,062 ∙76,86∙5,952= = -168,70	-0,030 ∙76,86∙6,152= = -87,21	-0,030 ∙76,86∙6,152= = -87,21
3		0,009 ∙76,86∙5,952= = 24,49	-0,038 ∙76,86∙5,952= = -103,40	-0,061 ∙76,86∙6,152= = -177,33	-0,061 ∙76,86∙6,152= = -177,33
4		-0,026 ∙76,86∙5,952= = -70,75	-0,117 ∙76,86∙5,952= = -318,36	-0,105 ∙76,86∙6,152= = -305,24	-0,043 ∙76,86∙6,152= = -125,0
5	Загружение 1+2	-132,61	-297,03	-203,99	-203,99
6	Загружение 1+3	-10,16	-138,73	-294,11	-294,11
7	Загружение 1+4	-105,4	-446,69	-422,02	-241,78

Таблица 2 – Результаты вычисления изгибающих моментов


3.2.1 Пролетные моменты и поперечные силы в ригелях
Схема 1+2

- усилия в 1 пролете:

Сила - поперечная

Q₁₂=ql/2+(M₁₂- M₂₁)/l=113,11∙5,95/2+(132,61 – 297,03)/5,95=308,87кН

Q₂₁=ql/2+(M₂₁- M₁₂)/l=113,11∙5,95/2+(297,03 – 132,61)/5,95=364,14кН

изгибающий момент в пролете

M_l1=ql²/8 - (M₁₂+ M₂₁)/2=113,11·5,95²/8 - (132,61+297,03)/2=285,73кНм;

- усилия во 2 пролете:

поперечные силы

Q₂₃= Q₃₂=q_gl/2+(M₂₃-M₃₂)/l=36,25·6,15/2+(203,99– 203,99)/6,15 = 111,47 кН/м;

изгибающий момент в пролете

M_l2=q_gl²/8 - M₂₃=36,25·6,15²/8 – 203,99= -32,61кНм.

Схема 1+3

- усилия в 1 пролете:

Q₁₂=q_gl/2+(M₁₂- M₂₁)/l=36,25·5,95/2+(10,16 – 138,73)/5,95=86,24 кН

Q₂₁=q_gl/2+(M₂₁- M₁₂)/l=36,25·5,95/2+(138,73-10,16)/5,95=129,45кН

изгибающий момент в пролете

M_l1=q_gl²/8 - (M₁₂+ M₂₁)/2=36,25·5,95²/8 - (10,16+138,73)/2=85,97 кНм;

- усилия во втором пролете (погонная нагрузка q):

поперечные силы

Q₂₃= Q₃₂=ql/2+(M₂₃-M₃₂)/l=113,11·6,15/2+(294,11 – 294,11)/6,15 = 348,81кН/м;

изгибающий момент в пролете

M_l2=ql²/8 - M₂₃=113,11·6,15²/8 – 294,11=240,65 кНм.

Схема 1+4

- усилия в первом пролете (погонная нагрузка q):

поперечные силы

Q₁₂=ql/2+(M₁₂- M₂₁)/l=113,11·5,95/2+(105,4 – 446,69)/5,95=279,14кН

Q₂₁ =ql/2+(M₂₁- M₁₂)/l=113,11·5,95/2+(446,69 – 105,4)/5,95=393,86кН

изгибающий момент в пролете

M_l1=ql²/8 - (M₁₂+ M₂₁)/2=113,11·5,95²/8 - (105,4+446,69)/2=224,5 кНм;

- усилия во втором пролете (погонная нагрузка q):

поперечные силы

Q₂₃=ql/2+(M₂₃-M₃₂)/l=113,11·6,15/2+(422,02 – 241,78)/6,15=377,12 кН

Q₃₂=ql/2+(M₃₂-M₂₃)/l=113,11·6,15/2+(241,78 – 422,02)/6,15=318,51кН

Момент

M_l2=ql²/8 - (M₂₃+ M₃₂)/2=113,11·6,15²/8 -(422,02+241,78)/2=202,86кНм.

3.2.2 Перераспределение моментов под влиянием образования пластических шарниров
Моментов на опоре 2:

слева

∆M₂₁=0,3∙446,69=134,01 кНм.

справа

∆M₂₃=∆M₂₁- (M₂₁ - M₂₃)=134,01 - (446,69 – 422,02) = 109,34 кНм.

Момент 1+4:

∆M₁₂= - (M₁₂¹⁺² - M₁₂¹⁺⁴)= - (132,61 – 105,4) = - 27,21 кНм;

∆M₃₂= - (M₃₂¹⁺³ - М_з2¹⁺⁴)= - (294,11 – 241,78) = - 52,33 кНм.

Моменты на эпюре 1+4:

М₁₂= - 105,4 – 27,21 = - 132,61 кНм;

М₂₁= - 446,69 + 134,01 = - 312,68 кНм;

М₂₃= - 422,02 + 109,34 = - 312,68 кНм;

M₃₂= - 241,78 – 52,33 = - 294,11 кНм;

Пролетные моменты на эпюре выровненных моментов 1+4 составили

М_l1= 224,5 + 53,4 = 277,9 кНм;

М_l2= 202,86 + 39,43 = 242,29 кНм;

Расчетными моментами в пролетах остаются: в первом - М_l2 = 285,73 кНм загружения 1+2, во втором пролете –М_l2 = 240,65 кНм загружения 1+3.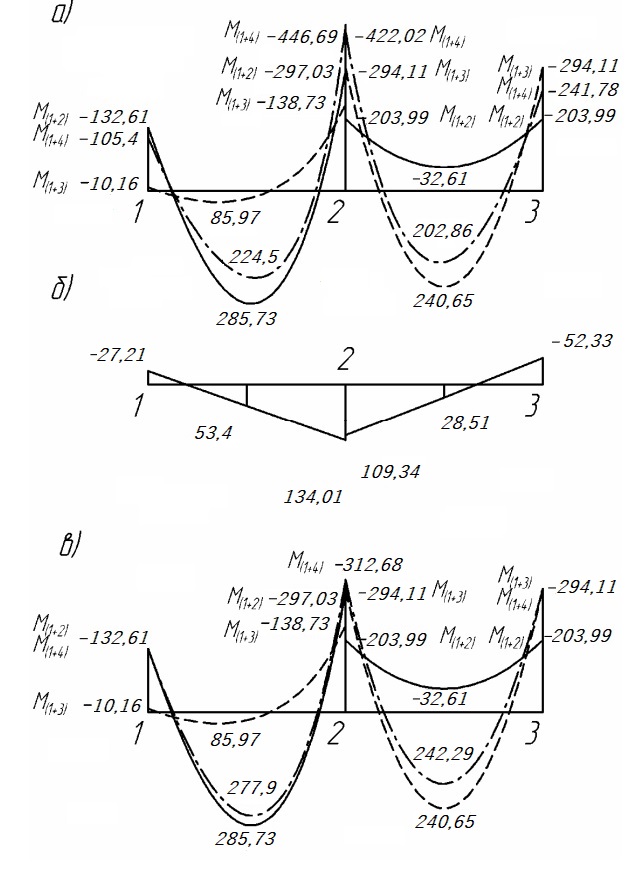



Рис. 2. Эпюры изгибающих моментов
Опорные моменты ригеля на грани:

Крайней колонны M₍₁₂₎₁:

- Схема 1+2

M_(12),l= - (M₁₂– Q₁₂∙h_col/2) = - (132,61 – 308,87·0,4/2) = - 70,85 кНм;

- Схема 1+3

M_(12),l= - (M₁₂– Q₁₂∙h_col/2) = - (10,16 – 86,24·0,4/2) = - 7,09 кНм;

- Схема 1+4

Q₍₁₂₎ = q∙l/2+(M₁₂- M₂₁)/l= 113,11·5,95/2+(132,61 – 446,69)/5,95 = 283,72 кНм;

M₍₁₂₎₁= - (M₁₂– Q₁₂∙h_col/2) = - (132,61 – 283,72·0,4/2) = - 75,87 кНм;

Средней колонны слева M_(21),1:

- Схема 1+2

M_(21),1= - (M₂₁- Q₂₁∙h_col/2) = - (297,03 – 364,14·0,4/2) = - 224,2 кНм;

- Схема 1+3

M_(21),1= - (M₂₁ – Q₂₁∙h_col/2) = - (138,73 – 129,45·0,4/2) = - 112,84 кНм;

- Схема 1+4

Q₍₂₁₎ = q∙l/2+(M₂₁– M₁₂)/l = 113,11·5,95/2+(312,68 – 132,61)/5,95 = 366,77 кНм;

M_(21),1= - (M₂₁- Q₂₁∙h_col/2) = - (312,68- 366,77 ·0,4/2) = - 239,33 кНм;

Средней колонны справа М₍₂₃₎₁:

- Схема 1+2

M_(23),1= - (M₂₃- Q₂₃xh_col/2) = - (203,99 – 111,47·0,4/2) = - 181,7 кНм;

- Схема 1+3

M_(23),1= - (M₂₃- Q₂₃xh_c0l/2) = - (294,11 – 348,81·0,4/2) = - 224,35 кНм;

- Схема 1+4

Q₍₂₃₎ = qxl/2+(M₂₃-M₃₂)/l = 113,11·6,15/2+(312,68- 294,11)/6,15 = 350,83 кНм;

M₍₂₃₎₁= - (M₂₃- Q₂₃xh_col/2) = - (312,68 – 350,83·0,4/2) = - 242,51 кНм;