_ЖБК2 КП. Курсовой проект по учебному курсу Железобетонные и каменные конструкции 2 Вариант 1С, 2Д, 3т студент
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
2.3 Характеристики прочности бетона и арматурыДля бетона тяжелого класса В25: Еb = 30103 МПа; Rb = 14,5МПа; Rbt = 1,05 МПа; R 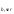 = 18,5 МПа; R = 18,5 МПа; R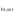 = 1,55 МПа; = 1,55 МПа;Для арматуры класса А240: Rsw = 170МПа,Еs = 2105МПа; Для арматуры класса В500: Rs = 415МПа,Еs = 2105МПа; Для арматуры класса А-800: Rs = 695 МПа, Rsn = 800МПа, Еs = 2105МПа. Величина предварительного напряжения арматуры: 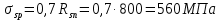 2.4 Расчет ребристой плиты перекрытия по 1-ой группе предельных состояний 2.4.1 Расчет плиты на прочность по нормальному сечениюРасчетный изгибающий момент равен М = 115,51 кНм. Сечение тавровое, полка находится в сжатой зоне. Сечение рассчитывается как прямоугольное. Вычисляется коэффициент: 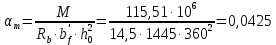 Высота относительная сжатой зоны бетона: 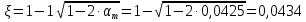 Высота сжатой зоны бетона: 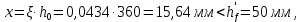 Граничная высота сжатой зоны: 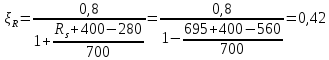 Рабочая площадь арматуры 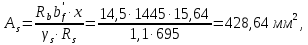 где 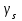 =1,1, так как =1,1, так как 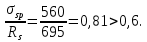 Принимаем арматуру 218 мм с общей площадью As = 509 мм2. 2.4.2 Расчет армирования полки ребристой плитыПлита с поперечными ребрами, отношение пролетов полки l2/l1=1300/1245 = 1,044 < 2, значит, полка рассчитывается как плита, защемленная по контуру. Нагрузка на полку плиты: (g + v)γn= (3,49 + 12,6)·1 = 16,09 кН/м, гдеg = gпола + gполки = (2,11 + 25·0,05·1,1) = 3,49 кН/м. Уравнение моментов в защемленной плите: 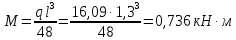 . .Рабочая высота сечения h0= h - а = 50 - 15 = 35 мм; 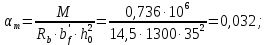 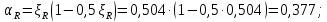 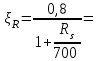 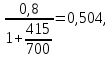 αm=0,032< αR=0,377, это означает, что установка арматуры в сжатой зоне не нужна. 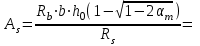 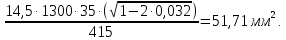 Принимаем сетки с шагом 200 мм со стержнями 4 мм с общей площадью As = 88мм2. 2.4.3 Геометрические характеристики приведенного сеченияКоэффициент приведения: 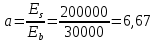 Площадь бетонного сечения: 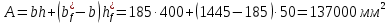 . .Площадь приведенного сечения:  . .Статический момент площади приведенного сечения: Sred= Σ(Ai∙ γi) =185∙ 400 ∙ 200 + (1445 - 185) ∙ 50∙ 375 + 6,67∙ 509 ∙ 40 = 38560801,2 мм3.  Рис. 1. Схема геометрических характеристик приведенного сечения Расстояние от нижней грани до центра тяжести приведенного сечения:  . .Момент инерции: 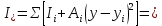 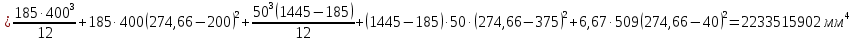 . .2.4.4 Потери предварительного напряжения в арматуре Первые потери: - от релаксации напряжений: sp1 = 0,03∙sp = 0,03∙560 = 16,8 МПа Усилия обжатия:  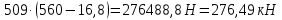 Эксцентриситет усилия предварительного обжатия: еор(1) = уsp = у - ар 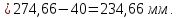 Максимальное сжимающее напряжение: 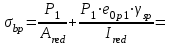 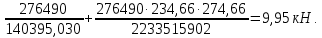 Условие σbp≤ 0,9Rbp = 0,9∙ 17,5 = 15,75 МПа выполняется, где Rbp= 0,7В = 0,7∙25 = 17,5 МПа. Вторые потери от предварительного напряжения: потери от усадки: Δσsp5 = eb,sh ・ Es= 0,0002 ∙ 200000 = 40 МПа; потери от ползучести: 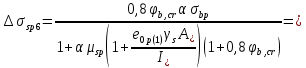 . .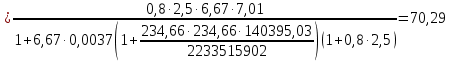 МПа МПаμsp = 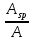 = = 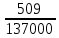 = 0,0037 = 0,0037Напряжение в бетоне: 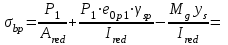 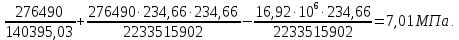 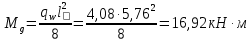 . .qw =2,5∙ 1,485∙ 1,1 = 4,08кНм Сумма вторых потерь: ∆σsp(2) = ∆σsp(5) +∆σsp(6) = 40 + 70,29 = 110,29 МПа Сумма первых и вторых потерь: ∆σsp1(1) +∆σsp2(2) = 16,8 + 110,29 = 127,09 МПа Предварительные напряжения: ∆σsp2 = σsp - ( ∆σsp1(1) +∆σsp2(2)) = 560 – 127,09 = 432,91 МПа Усилия суммарных потерь: P = ∆σsp2∙Asp = 432,91∙509 = 220351,19 Н = 220,35 кН. 2.4.5 Расчет прочности бетонной полосы Расчет полосы бетона на прочность: 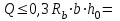 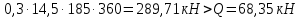 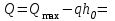 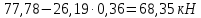 Таким образом, наблюдаем обеспеченность прочности для полосы бетона. 2.4.6 Расчет прочности ребристой плиты по наклонным сечениямДля поперечного расположения выбираем стержни из арматуры класса А240 с диаметром 6 мм. Общая площадь поперечного сечения составит 57 мм2. Исходя из соображений конструктивного характера максимальные значения шага для стержней составят: 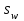 ≤ h0 /2 = 360/2 = 180 мм. ≤ h0 /2 = 360/2 = 180 мм.Шаг 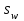 = 150 мм. = 150 мм.Условие прочности Q ≤ Qb + Qsw, Усилие в хомутах на единицу длины плиты: 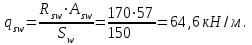 Коэффициент φn равен: 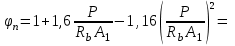  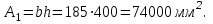 Хомуты следует учитывать, если выполняется условие: 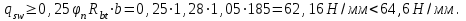 Условие соблюдено. Сила, которая воспринимается бетоном с наклонным сечением равна: 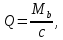 где  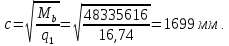 Получаем расчетное значение временной нагрузки: q1 = q – 0,5qv = 26,19 – 0,5 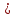 18,9 = 16,74 кН/м, 18,9 = 16,74 кН/м,где qv= vbнγn = 12,6 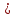 1,5 1,5 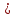 1,0 = 18,9 кН/м. 1,0 = 18,9 кН/м.Условие проверки 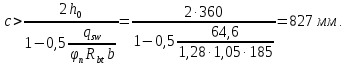 Условие выполняется, значит с не пересчитывается. По конструктивным требованиям имеем: c ≤ 3h0 = 3⋅360 = 1080 мм. 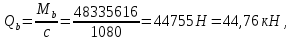 отсюда Qbне более чем: Qmax = 2,5Rbt bh0 = 2,5 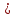 1,05 1,05 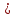 185 185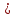 360 = 174825 Н = 174,83 кН 360 = 174825 Н = 174,83 кНи не менее чем: Qb,min = 0,5φn Rbt bh0 = 0,5 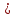 1,28 1,28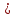 1,05 1,05 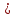 185 185 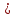 360 = 44755,2 Н = 44,76 кН. 360 = 44755,2 Н = 44,76 кН.Условие выполняется. Определение усилия: Qsw= 0,75qsw c0 = 0,75 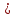 64,6 64,6 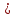 720 = 34884 Н = 34,88 кН, 720 = 34884 Н = 34,88 кН,где с0 = 2h0 = 2 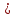 360 = 720 мм – длина проекции наклонного сечения. 360 = 720 мм – длина проекции наклонного сечения.Наклонное сечение: Q = Qmax – q1c = 77,78 – 16,74 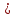 1,08 = 59,7 кН. 1,08 = 59,7 кН.В соответствии с условием Q ≤ Qb + Qsw, 59,7 < 44,76 + 34,88 = 79,64 кН, можем сделать вывод о том, что прочность обеспечена. Максимально допустимый шаг хомутов, учитываемых в расчете, определяем как:  Принятый шаг хомутов удовлетворяет требованию. Шаг хомутов возможно увеличить с уменьшением силы.  ≤ 0,75 h0 = 0,75·360 = 270 мм. ≤ 0,75 h0 = 0,75·360 = 270 мм.Примем шаг 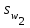 = 250 мм. = 250 мм.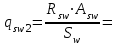 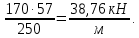 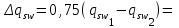 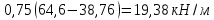 Так как 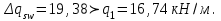 Длина участка с шагом qsw1 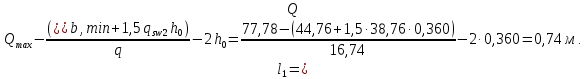 2.5 Расчет ребристой плиты по второй группе предельных состояний 2.5.1 Расчет по образованию трещин, нормальных к продольной оси Момент образования трещин: 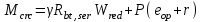 , , 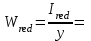 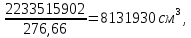 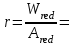 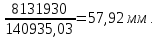 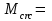 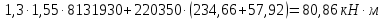 Т.к. M = 96,71 кНм > Mcrc = 80,86 кНм, необходимо осуществить расчет на раскрытие трещин. 2.5.2 Расчет ширины раскрытия трещин Расчет приращения напряжения от действия постоянных и длительных нагрузок σs = σs1, т. е. принимая Мs = Ml = 80,27 кНм. esp = 0, 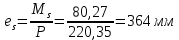 Рабочая высота сечения равна ho = 360мм, 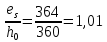 . .А/sр = А/s =0, получаем 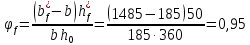 Коэф. приведения получается 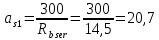 , тогда , тогда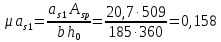 z = ξh0 = 0,858 ∙ 360 = 308,9 мм,  Отсюда определяем σs,crc при моменте Ms= Mcrc = 80,86 кНм 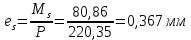 , , 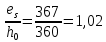 , находим ξ = 0,86 (справочное значение), отсюда плечо , находим ξ = 0,86 (справочное значение), отсюда плечо z = ξh0 = 0,86 ∙ 360 = 309,6 мм, 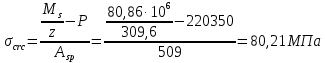 Определение aS,tot при моменте Ms = Mtot = 96,71 кНм. 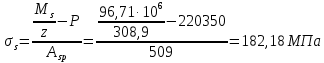 Условие проверки A > t, при t = 0,59 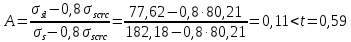 Так как А < t, то acrc=acrc1+acrc2 -acrc3 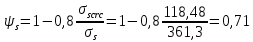 Высота зоны растянутого бетона: 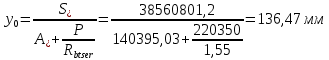 . .а если учесть неупругую деформацию растянутого бетона: yt = k ∙ y0 = 0,95∙136,47 = 129,65мм. Так как yt > 2а = 2·40 = 80 мм, получаем уt = 129,65 мм, тогда Abt= byt= 185∙129,65 = 23984,81 мм2 и расстояние тогда будет: 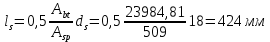 Считаем ls > 400 мм и ls < 40d = 40∙18 = 720 мм, принимаем ls = 424 мм. 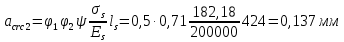 acrc =acrc2(1 + 0,4A) = 0,137(1 + 0,4·0,11) = 0,143 < 0,3мм. Таким образом, трещиностойкость обеспечна. 2.5.3 Расчет прогиба ребристой плиты перекрытияОпределяем кривизну при моменте М = Ml = 80,27 кНм. es/h0 = 1,01, φf = 0,95 ψs = 0,71. Действие нагрузки при условии нормальной влажности: 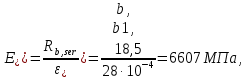 b1,red= 28  10-4 при влажности 70% ≥ W ≥ 40 %. 10-4 при влажности 70% ≥ W ≥ 40 %. 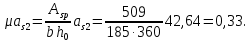 При φf = 0,95, es/h0 = 1,01 и μαs2 = 0,33, находим φс= 0,558, тогда кривизна равна: 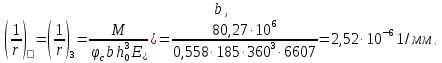 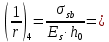 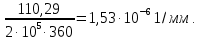 Полная кривизна равна 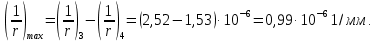 Прогиб плиты находим, принимая S = 5/48: 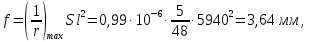 что меньше fult = 5940/200 = 29,7 мм. что меньше fult = 5940/200 = 29,7 мм.Жесткость достаточная. |
