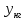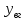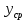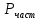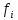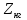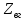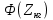Курсовая работа Трофименко В.А. ФКБВ-01-19..bb. Курсовой проект (работа) по дисциплине Основы надежности электронных средств (наименование дисциплины) Тема курсового проекта (работы) Рассчитать оптимальное (среднее) значение входного сопротивления унч (у r 1
 Скачать 152 Kb. Скачать 152 Kb.
|
 Кафедра «Конструирование и технология электронных средств» КУРСОВОЙ ПРОЕКТ (РАБОТА) по дисциплине «Основы надежности электронных средств» (наименование дисциплины) Тема курсового проекта (работы) «Рассчитать оптимальное (среднее) значение входного сопротивления УНЧ (у=R1||R2 /R4)» (наименование темы)
Фрязино 2021 г.
Кафедра «Конструирование и технология электронных средств» Утверждаю Заведующий кафедрой____________ «___» _______2021 г. ЗАДАНИЕ на выполнение курсового проекта (работы) по дисциплине «Основы надежности РЭС» Студент Трофименко Вадим Александрович Группа ФКБВ-01-19 1. Тема «Рассчитать оптимальное (среднее) значение входного сопротивления УНЧ (у=R1||R2 /R4)» 2. Исходные данные: Таблицы с расчетными данными Перечень вопросов, подлежащих разработке, и обязательного графического материала: Срок представления к защите курсового проекта (работы): до «11» июня 2021
СОДЕРЖАНИЕ
Задачи. ………………………....………....………....…...………....……....3 Расчёт математического ожидания и дисперсии. .…...……..…....……....5 Расчёт доверительных интервалов……....………....…...………....……....5 Построение гистограммы распределения выходного параметра Y…......7 Вероятностные характеристики………....…………………………....…...10 Критерии согласия…………....………....……..…....…...………....…...…10 Линейная зависимость……....………....…………....…...………....……...11 Метод наименьших квадратов………....……...……………………....…..12 Заключение…………………......………....………....…...………....……....15 Реферат………………....………….……....………....…...………....……....16 Литература………………...........………....………....…...………....……....17 ВВЕДЕНИЕВ современном мире усилители низкой широко применяются для усиления сигналов, несущих звуковую информацию, но также применяются и для усиления информационных сигналов в различных сферах. Усилитель низкой частоты – электроприбор, предназначенный для усиления электрических колебаний, соответствующих слышимому человеком диапазону частот, таким образом к данным усилителям предъявляются требования усиления в диапазоне частот от 20 до 20000 Гц. Целью данной работы является построение модели оптимального значения входного сопротивления УНЧ (y = R1||R2/R4). Задачи По результатам эксперимента построить экспериментальное распределение величины Y и найти её числовые характеристики. Разработать вероятностную модель выходного параметра 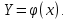 По результатам эксперимента, определить оценки математического ожидания и дисперсии для величины 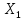 , найти величину доверительного интервала для заданной доверительной вероятности. , найти величину доверительного интервала для заданной доверительной вероятности.По критерию согласия 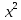 определить вероятность гипотезы о том, что величина Y имеет нормальное распределение. определить вероятность гипотезы о том, что величина Y имеет нормальное распределение.Доказать возможное существование функциональной зависимости 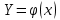 используя метод наименьших квадратов, а также определить коэффициенты этой линейной функции. используя метод наименьших квадратов, а также определить коэффициенты этой линейной функции.Таблица 1. Результаты эксперимента
Расчёт математического ожидания и дисперсии Математическое ожидание означает среднее значение случайной величины, а дисперсия означает рассеяние и характеризует разброс случайной величины относительно центра распределения. Математическое ожидание для X и Y выражается следующими формулами: 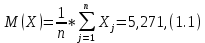 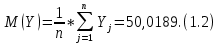 Откуда дисперсия для X и Y равна: 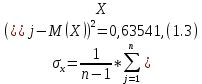 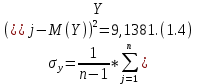 Расчёт доверительных интервалов Доверительным называется интервал, в который попадают измеренные в эксперименте значения, соответствующие доверительной вероятности. Доверительная вероятность – вероятность, с которой в условиях данного эксперимента полученные экспериментальные данные можно считать надёжными (достоверными), называют доверительной вероятностью или надёжностью. В результате того, что нам известна не вся генеральная совокупность, всего лишь 50 опытов, невозможно точно оценить значение 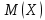 , рассчитанное в пункте 1. Поэтому значение , рассчитанное в пункте 1. Поэтому значение 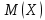 рассчитано с погрешностью рассчитано с погрешностью 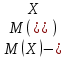 . Далее необходимо найти интервал, вероятность попаданий в который случайной величины равнялась бы . Далее необходимо найти интервал, вероятность попаданий в который случайной величины равнялась бы 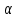 : :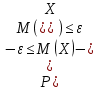 где 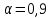 - доверительная вероятность. - доверительная вероятность.Введём следующую величину в это неравенство: 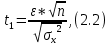 Выражение для вероятности 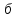 равно: равно: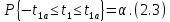 Данная вероятность выражается через функцию распределения Стьюдента S(t): 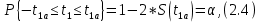 где 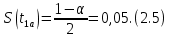 Из таблицы [2] находим значение 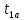 соответствующее 0,05 и n = 50. Откуда соответствующее 0,05 и n = 50. Откуда 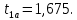 После чего подставляем это в формулу и находим После чего подставляем это в формулу и находим 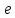 : :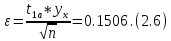 Исходя из этого доверительный интервал математического ожидания равен: 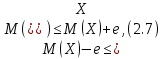 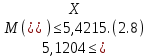 Доверительный интервал для среднеквадратичного отклонения 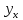 : :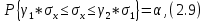 где 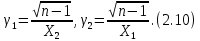 Значения 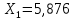 и и 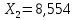 находятся в таблицы. Отсюда доверительный интервал среднеквадратичного отклонения равен: находятся в таблицы. Отсюда доверительный интервал среднеквадратичного отклонения равен: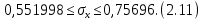 Гистограмма В данной части курсового проекта необходимо построить гистограмму распределения выходного параметра Y. Для построения гистограммы необходимо её разбить на разряды. Оптимальное значение разрядов для 50-ти опытов – m=8. Для того, чтобы разбить значения Y на 8 разрядов, необходимо знать минимальное и максимальное значения выходного параметра Y: 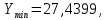 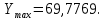 Ширина разряда определяется по следующей формуле: 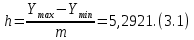 Находим границы разрядов. Нижняя граница находится по формуле: 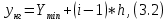 где i– порядковый номер разряда. Верхняя граница: 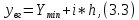 середина интервала i – го разряда: 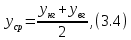 частотность разряда: 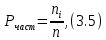 где 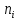 – количество попаданий в i–ый разряд. – количество попаданий в i–ый разряд.Высоты гистограммы i– го разряда: 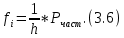 Получившиеся результаты разбиения на разряды показаны на рисунке 1. 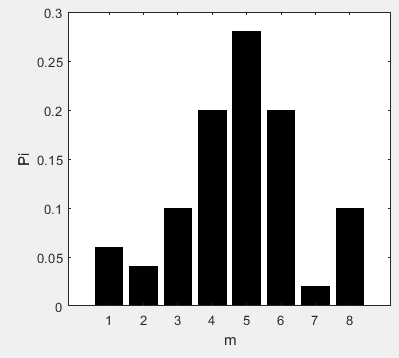 Рисунок 1. Гистограмма разбиения выборок. Данная гистограмма, показывает количество попаданий значений Yв i-ый разряд. Проведя огибающую, можно составить примерное представление о виде плотности вероятности исследуемой случайной величины. Таким образом на основании рисунка 1 можно сказать, что теоретический закон распределения имеет вид нормального закона распределения. Далее нужно найти значения функции Лапласа: 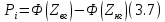 где 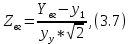 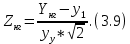 В таблице 2 представлены получившиеся результаты. Таблица 2. Результаты расчёта
Вероятностные характеристики Центральный момент первого порядка равен: 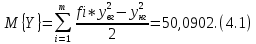 Центральный момент второго порядка: 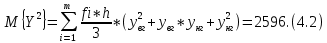 Дисперсия: 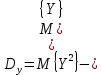 Критерии согласия Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределения случайным или значимым, то есть согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются. Далее находим 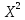 критерия согласия по формуле: критерия согласия по формуле: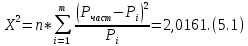 После чего необходимо узнать число степеней свободы: 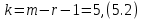 где r – число параметров испытываемого закона распределения. В нашем случае r = 2. По табличным значениям 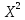 и k находим вероятность и k находим вероятность 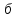 гипотезы о том, что величина Y имеет нормальное распределение: гипотезы о том, что величина Y имеет нормальное распределение: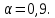 Линейная зависимость Докажем возможность существования линейной зависимости Y от X. Таким образом предположим, что Y зависит линейно от X, тогда: 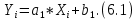 Найдём оценку математического ожидания 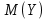 : :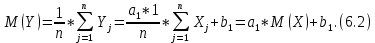 Оценка дисперсии: 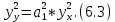 Исходя из выражения выше: 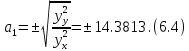 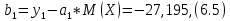 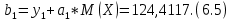 Из выше полученных значений получается, что существует линейная зависимость между случайными величинами Y и X: 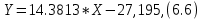 или 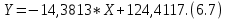 Метод наименьших квадратов. Случайные значения 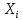 и и 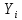 связаны линейной зависимостью связаны линейной зависимостью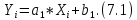 Далее нужно найти величины 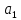 и и 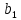 их условия, что сумма их условия, что сумма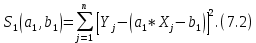 принимает наименьшее значение. Условие минимума для 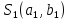 : :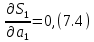 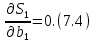 Подставим эти формулы в выражение для 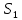 : :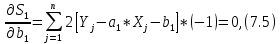 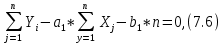 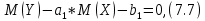 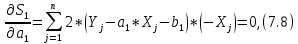 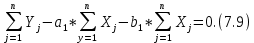 Все члены этого уравнения разделим на n и обозначим: 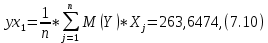 После всех манипуляций получится уравнение: 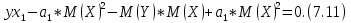 Отсюда 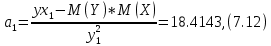 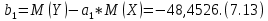 Исходя из этого, линейная зависимость примет вид: 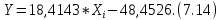 В этом случае мы получили более точные значения, чем в пункте 6. 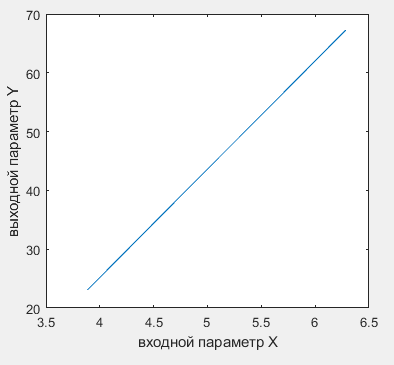 Рисунок 2. График линейной зависимости выходного параметра Y от входного X. ЗаключениеВ работе были получена оценка математического ожидания, найдены величины доверительных интервалов для математического ожидания и дисперсии при заданной доверительной вероятности, рассчитана и построена гистограмма результата разбиения выборки на разряды, рассчитана линейная зависимость методом наименьших квадратов и рассчитаны параметры линейной функции. РефератТема курсового проекта «Построение модели оптимально значения входного сопротивления УНЧ (y = R1||R2/R4)». Курсовой проект состоит из введения, расчётно-пояснительной записки и заключения. Расчётно-пояснительная записка содержит результаты опытов, расчёт оценки математического ожидания, дисперсии и доверительных интервалов. Доказательство того, что параметр Y имеет нормальное распределение. Доказательство существования линейной зависимости Y от X методом наименьших квадратов. Курсовая содержит таблиц 2, библиографий 5. Общий объём пояснительной записки составляет 17 листов. ЛитератураСправочник конструктора РЭА. Общие принципы конструирования. Под ред. Р.Г. Варламова, М., «Сов.радио», 1980. Ненашев А.П., Коледов Л.А. Основы конструирования микроэлектронной аппаратуры. М., «Радио и связь», 1981. Беккер П., Йенсен Ф. Проектирование надежных электронных средств. М., «Сов.радио», 1977. Глудкин О.П., Обичкин Ю.Г., Блохин В.Г. Статистические методы в технологии производства радиоэлектронной аппаратуры. М., «Энергия», 1977. Ильин В.Н. Основы автоматизации схемотехнического проектирования. М., «Энергия», 1979. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||