Линейное программирование. Задачи линейного программирования
 Скачать 89.93 Kb. Скачать 89.93 Kb.
|
|
Введение Линейное программирование — область математического программирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными. Программирование в управлении можно представить как процесс распределения ресурсов. Существует ряд различных методов, основанных на идеях математического программирования, однако, наиболее широкое применение нашел метод линейного программирования. Применение методов линейного программирования актуально в сегодняшнее время, так как использование математических моделей является важным направлением совершенствования планирования и анализа деятельности компании. Представление данных в виде математической модели позволяет конкретизировать информацию, создавать и моделировать варианты, выбирать оптимальные решения. Актуальность линейного программирования и обусловила выбор темы данной курсовой работы. Значимость выбранного вопроса определяется также тем, что использование метода линейного программирования представляет собой важность и ценность – оптимальный вариант выбирается из достаточно значительного количества альтернативных вариантов. Также все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями Цель курсовой работы – на практическом примере продемонстрировать использование методов линейного программирования. Задачи работы обусловлены ее целью: Во-первых, раскрыть теоретическое содержание данной темы. Во-вторых, сформулировать и найти оптимальное решение задач с помощью средств MS Excel. Задачи линейного программирования 1. С помощью средств Excel найти решение задачи линейного программирования L(Х) = 14х 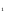 -9х2 -х4 +6,4х5 —> min; -9х2 -х4 +6,4х5 —> min;0 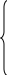 ,9 х ,9 х + 10х2 -28х4 +5х5 + 10х2 -28х4 +5х5  245, 245, 0,8 х 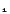 + 1,7х2 -0,2х3 -0,5х4 =9, + 1,7х2 -0,2х3 -0,5х4 =9,6 х 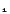 + 4х3 - 7х4 + 6,3х5 + 4х3 - 7х4 + 6,3х5  54, 54, 8 х 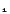 +6,2х2 -4,8х4 +2,9х5 +6,2х2 -4,8х4 +2,9х5  17, 17,x 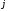  0, (j = 0, (j = 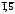 ). ).2. Мебельный комбинат выпускает книжные полки А из натурального дерева со стеклом, полки В1 из полированной ДСП (древесно-стружечной плиты) без стекла и полки В2 из полированной ДСП со стеклом. Габариты полок А, В1 и В2 следующие: длина 1100 (d) мм, ширина 250 (w) мм, высота 300 (h) мм/ Размер листа ДСП 2x3 м.   h w d Габариты полок, выпускаемых мебельным комбинатом При изготовлении полок А выполняются следующие работы: столярные, покрытие лаком, сушка, резка стекла, упаковка. Все операции, производимые в ходе столярных работ и упаковки, выполняются вручную. Полки В1 и В2 поставляются в торговую сеть в разобранном виде. За исключением операции упаковки, все остальные операции (производство комплектующих полки, резка стекла) при изготовлении полок В1 и В2, выполняются на специализированных автоматах. Трудоемкость столярных работ по выпуску одной полки А составляет 3,2 (Тр1) ч. Производительность автомата, покрывающего полки А лаком - 2 (Пр1) полок в час, автомата, режущего стекло - 180 (Пр2) стекол в час. Сменный фонд времени автомата для покрытия лаком – 7,4 (ФВ1) ч, автомата для резки стекла - 7,1 (ФВ2) ч. Сушка полок, покрытых лаком, происходит в течение суток в специальных сушилках, вмещающих 55 (VI) полок. На упаковку полки А требуется 6 (Тр2) минуты. В производстве полок заняты 27 (Р1) столяров и 7 (Р2) упаковщиков. Производительность автомата, производящего комплектующие полок В, и В2, равна 7 (Прз) полки в час, а его сменный фонд времени равен 7,8 (ФВ3) ч, трудоемкость упаковочных работ составляет 9 (Тр3) мин для полки В1 и 10 (Тр4) мин для полки В2. От поставщиков комбинат получает в месяц 415 (Z1) листов полированной ДСП, 215 (Z2) листов ДВП (древесно-волокнистой плиты), а также 240 (Z3) листов стекла. Из каждого листа ДВП можно выкроить 6 (К1) задних стенок полок В1 и В2, а из каждого листа стекла - 13 (К2) стекол для полок А и В2. Склад готовой продукции может разместить не более 370 (V2) полок и комплектов полок, причем ежедневно в торговую сеть вывозится в среднем 72(N) полок и комплектов. На начало текущего месяца на складе осталось 80 (Ост) полок, произведенных ранее. Себестоимость полки А равна 150 (С1) руб., полки В без стекла - 120 (С2) руб., со стеклом - 134 (Сз) руб. Маркетинговые исследования показали, что доля продаж полок обоих видов со стеклом составляет не менее 43% (Д) в общем объеме продаж, а емкость рынка полок производимого типа составляет около 1100 (Vз) штук в месяц. Мебельный комбинат заключил договор на поставку заказчику 50 (З) полок типа В2 в текущем месяце. Составьте план производства полок на текущий месяц. Известны цены реализации полок: полка А - 192 (Ц1) руб., полка В без стекла - 154 (Ц2) руб., полка В со стеклом - 147 (Ц3) руб.
3 варианта раскроя ДСП, 8 ч в смене; работа в 1 смену; 22 рабочих дня в месяц. 3. На складах хранится мука, которую необходимо завезти в хлебопекарни. Номера складов и номера хлебопекарен даны в таблице 1. Текущие тарифы перевозки муки [руб./т], ежемесячные запасы муки [т/мес] на складах и потребности хлебопекарен в муке [т/мес] указаны в табл. 2. При этом необходимо учитывать, что из-за ремонтных работ временно нет возможности перевозить муку с некоторых складов в некоторые хлебопекарни. В табл. 1это показано в графе "Запрет перевозки" в формате № склада х № хлебопекарни. Например, «2x3» обозначает, что нельзя перевозить муку со склада № 2 в хлебопекарню № 3. Кроме того, необходимо учесть, что некоторые хлебопекарни имеют договоры на гарантированную поставку муки с определенных складов. В табл. 1 это показано в графе "Гарантированная поставка" в формате № склада х № хлебопекарни = объем поставки. Например, «1x4=40» обозначает, что между складом № 1 и магазином № 4 заключен договор на обязательную поставку 40 т муки. Необходимо организовать поставки наилучшим образом, учитывая, что мука хранится и транспортируется в мешках весом по 50 кг. Таблица 1 Номер склада, хлебопекарни, запрещенные или гарантированные поставки
Таблица 2 Запасы, потребности и тарифы перевозок
2. Теоретическая основа линейного программирования 2.1.Постановка задачи Постановка практической задачи ЛП включает следующие основные этапы: определение показателя эффективности, переменных задачи, задание линейной целевой функции S(x), подлежащей минимизации или максимизации, задание ограничений. Приведем сейчас общую математическую формулировку основной задачи линейного программирования. Дана система линейных уравнений с n неизвестными: a11 x1 + a11 x2 + …… + a11 xn  = = b1 , b1 ,a21 x1 + a22 x2 + …… + a2n xn  = = b2 , b2 ,am1 x1 + am2 x2 + …… + amn xn  = = bm , bm ,и линейная функция f = c1 x1 + c2 x2 +………+ cn xn (1.2) Требуется найти такое неотрицательное решение системы x1 ≥0, x2 ≥0, … … , xn ≥0 (1.3) при котором функция f принимает наименьшее значение. Уравнения (1.1) называют системой ограничений данной задачи; функцию f — целевой функцией (или линейной формой). 2.2.Методы решения задач линейного программирования 2.2.1. Симплекс – метод Симплекс метод - метод линейного программирования, который реализует рациональный перебор базисных допустимых решений, в виде конечного итеративного процесса, необходимо улучшающего значение целевой функции на каждом шаге. Применение симплекс-метода для задачи линейного программирования предполагает предварительное приведение ее формальной постановки к канонической форме с n неотрицательными переменными: (X1, ..., Xn), где требуется минимизация линейной целевой функции при m линейных ограничениях типа равенств. Среди переменных задачи выбирается начальный базис из m переменных, для определенности (X1, ..., Xm), которые должны иметь неотрицательные значения, когда остальные (n-m) свободные переменные равны 0. Целевая функция и ограничения равенства преобразуются к диагональной форме относительно базисных переменных, переменных, где каждая базисная переменная входит только в одно уравнение с коэффициентом 1: X0 + A0,m+1*Xm+1 + ... + A0,n*Xn = A0,0 X1 + A1,m+1*Xm+1 + ... + A1,n*Xn = A1,0 . . . . . . . . . . . . . . . . . . Xi + Ai,m+1*Xm+1 + ... + Ai,n*Xn = Ai,0 . . . . . . . . . . . . . . . . . . Xm + Am,m+1*Xm+1 + ... + Am,n*Xn = Am,0 Данная формальная модель задачи линейного программирования обычно задается в форме так называемой симплекс-таблицы, удобной для выполнения операций симплекс-метода: Симплекс-таблица
Верхняя строка симплекс-таблицы представляет целевую функцию задачи. Каждая строка симплекс-таблицы, кроме первой, соответствует определенному ограничению-равенству задачи. Свободные члены ограничений составляют крайний левый столбец таблицы. Слева от таблицы записаны текущие базисные переменные (X1, ..., Xm). Сверху от таблицы приведен набор всех переменных задачи, где Xm+1, ..., Xn - свободные переменные задачи. Преобразования таблицы надо производить до тех пор, пока не будет получена симплекс-таблица, которая одновременно является прямо и двойственно допустимой. Данный метод получил широкое распространение и большую популярность по сравнению с другими подходами, так как крайне редко на практике встречаются задачи трудные для симплекс-метода. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
