Линейное программирование. Задачи линейного программирования
 Скачать 89.93 Kb. Скачать 89.93 Kb.
|
|
2.2.2. Геометрический метод Применяется дя задач с двумя переменными. Метод решения состоит в следующем: Н  а плоскости Ох1х2 строятся прямые, которые задают соответствующие ограничения: а плоскости Ох1х2 строятся прямые, которые задают соответствующие ограничения:a11 x1 + a11 x2 + …… + a11 xn = b1 , a21 x1 + a22 x2 + …… + a2n xn = b2 , ………………………………………… am1 x1 + am2 x2 + …… + amn xn = bm . Находим множество всех точек х1,х2, удовлетворяющим всем неравенствам. Такое множество называется областью допустимых решений. Строим вектор 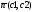 и перемещаем линию уровня, который задается уравнением: с1х1+с2х2 = const в направлении вектора и перемещаем линию уровня, который задается уравнением: с1х1+с2х2 = const в направлении вектора  до последней точки пересечения с ОДР. Эта точка и дает решение задачи Lmax = значению L в этой точки до последней точки пересечения с ОДР. Эта точка и дает решение задачи Lmax = значению L в этой точки2.3. Двойственная задача. Общая схема построения двойственной задачи. Если задана общая задача ЛП: 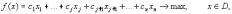 где D определяется системой уравнений и неравенств: 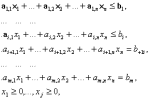 то двойственной по отношению к ней называется общая задача ЛП: 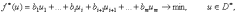 где D* определяется системой уравнений и неравенств:  Как следует из приведенной схемы при переходе от прямой задачи ЛП к двойственной: 1. Тип оптимума меняется на противоположный, т. е. максимум на минимум, и наоборот. 2. Вектор коэффициентов целевой функции c и столбец ограничений b меняются местами. 3. Матрица ограничений задачи А транспонируется. 4. Множество индексов переменных, на которые наложено условие неотрицательности в прямой задаче определяют номера ограничений, имеющих форму неравенств в двойственной задаче . 5. Множество номеров ограничений, имеющих форму неравенств в прямой задаче определяют множество индексов переменных, на которые накладывается условие неотрицательности, в двойственной задаче . Из приведенного определения вытекает важное свойство — симметричность отношения двойственности, т. е. задача, двойственная по отношению к двойственной, совпадает с прямой (исходной) задачей. ((D*)*, (f*)*)≡(D, f), Основные теоремы: Теорема 1. Если одна из двойственных задач имеет конечный оптимум, то другая также имеет конечный оптимум, причем экстремальные значения целевых функций совпадают Теорема 2 ( о дополняющей нежесткости). Для того чтобы план х* и у* являлись оптимальными решениями соответственно задач линейного программирования и двойственной к ним необходимо и достаточно, чтобы выполнялись следующие соотношения: 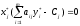 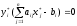 Теорема 3 (об оценках). Значение переменных 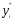 в оптимальном решении двойственной задачи представляет собой оценки влияния свободных членов bi в системе ограничения прямой задачи на величину целевой функции f(x*) в оптимальном решении двойственной задачи представляет собой оценки влияния свободных членов bi в системе ограничения прямой задачи на величину целевой функции f(x*)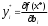 2.4. Транспортная задача. Одна из наиболее распространенных задач математического программирования — транспортная задача. В общем виде ее можно представить так: требуется найти такой план доставки грузов от поставщиков к потребителям, чтобы стоимость перевозки (или суммарная дальность, или объем транспортной работы в тонно-километрах) была наименьшей. Следовательно, дело сводится к наиболее рациональному прикреплению производителей к потребителям продукции (и наоборот). В простейшем виде, когда распределяется один вид продукта и потребителям безразлично, от кого из поставщиков его получать, задача формулируется следующим образом. Имеется ряд пунктов производства 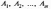 с объемами производства в единицу времени (месяц, квартал), равными соответственно с объемами производства в единицу времени (месяц, квартал), равными соответственно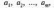 и пункты потребления и пункты потребления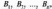 потребляющие за тот же промежуток времени соответственно потребляющие за тот же промежуток времени соответственно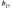 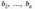 продукции. В случае, если решается закрытая (сбалансированная) задача, сумма объемов производства на всех пунктах-поставщиках равна сумме объемов потребления на всех пунктах-получателях: продукции. В случае, если решается закрытая (сбалансированная) задача, сумма объемов производства на всех пунктах-поставщиках равна сумме объемов потребления на всех пунктах-получателях: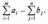 Кроме того, известны затраты по перевозке единицы продукта от каждого поставщика к каждому получателю — эти величины обозначаются  В качестве неизвестных величин выступают объемы продукта, перевозимого из каждого пункта производства в каждый пункт потребления, соответственно обозначаемые В качестве неизвестных величин выступают объемы продукта, перевозимого из каждого пункта производства в каждый пункт потребления, соответственно обозначаемые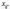 . .Тогда наиболее рациональным прикреплением поставщиков к потребителям будет такое, при котором суммарные затраты на транспортировку будут наименьшими: 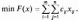 При этом каждый потребитель получает нужное количество продукта: 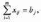 и каждый поставщик отгружает весь произведенный им продукт: 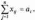 Как и во всех подобных случаях, здесь также оговаривается неотрицательность переменных: поставка от какого-то пункта производства тому или иному пункту потребления может быть равна нулю, но отрицательной, т. е. следовать в обратном направлении, быть не может. Рассмотрим таблицу. Строки транспортной таблицы соответствуют пунктам производства (в последней клетке каждой строки указан объем запаса продукта ai), а столбцы — пунктам потребления (последняя клетка каждого столбца содержит значение потребности bj). Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о перевозке из i-го пункта в j-й: в левом верхнем углу находится цена перевозки единицы продукта, а в правом нижнем — значение объема перевозимого груза для данных пунктов. Клетки, которые содержат нулевые перевозки (xi,j=0), называют свободными, а ненулевые — занятыми (xi,j>0).
Несбалансированную (открытую) транспортную задачу приводят к виду, показанному выше, искусственно: в модель вводятся так называемые фиктивный поставщик или фиктивный потребитель, которые балансируют спрос и потребление. В настоящее время разработано множество различных алгоритмов решения транспортной задачи: распределительный метод, метод потенциалов, дельта-метод, венгерский метод, метод дифференциальных рент, различные сетевые методы и т. д. Производственно-транспортная задача Это оптимизационная задача, при которой одновременно с установлением объема производства на отдельных предприятиях определяется и оптимальная схема размещения заказов (т. е. прикрепления поставщиков к потребителям). Она имеет особое значение для так называемых многотоннажных производств, где важен транспортный фактор (например, черные металлы, минеральные удобрения, нефтепереработка). Такие задачи математически могут быть представлены в двух видах: в сетевой и в матричной постановке. Будучи основанными на принципах транспортной задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. Пусть Х1, Х2, Х3, Х4, Х5 – неизвестные переменные Целевая функция: L(Х) = 14 х  -9 х2 - х4+6,4 х5—> min; -9 х2 - х4+6,4 х5—> min;Ограничения:g1: 0,9 х  + 10 х2-28х4 +5х5 + 10 х2-28х4 +5х5 245, 245,g2: 0,8 х 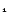 + 1,7х2 -0,2х3 -0,5х4 =9, + 1,7х2 -0,2х3 -0,5х4 =9,g3: 6 х 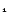 + 4х3 - 7х4 + 6,3х5 + 4х3 - 7х4 + 6,3х5  54, 54,g4: 8 х 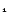 +6,2х2 -4,8х4 +2,9х5 +6,2х2 -4,8х4 +2,9х5  17, 17,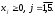 3.1.2.Ввод данных 1. Введем на рабочий лист Excel необходимые данные. В ячейке В5 запишем выражение целевой функции, а в ячейках В8:В11– левые части ограничений. 2.Командой Сервис, Поиск решения откройем диалоговое окно Поиск решения (рис. 2) и заполним его данными. В поле Установить целевую ячейку введем адрес целевой функции $В$5, в поле Изменяя ячейки - адреса $B$3:$E$3. Переведите переключатель Равной в положение минимальному значению. Чтобы ввести ограничения в окне Поиск решения нажмем кнопку Добавить и на экране появится диалоговое окно Добавление ограничения . 3. Начнем с первого ограничения. Установим курсор в поле Ссылка на ячейку и, выделяя на листе (рис.1) ячейку В8, введем ее адрес $B$8 в это поле. Кнопкой-стрелкой откроем список и выберем в нем знак <=. В поле Ограничение установите курсор и, выделяя на листе ячейку D8, введем ее адрес $ D $8 в это поле и нажмем кнопку Добавить. 4. Повторим действия п.3 и введем остальные ограничения $В$9=$D$9, $В$10<=$D$10, $В$11>=$D$11, реализующие граничные условия. После ввода последнего ограничения $F$11<=$H$11 вместо кнопки Добавить нажмем кнопку ОК. Таким образом, в окно Поиск решения (рис. 2) будут введены ограничения. 3.1.3. Решение задачи 1. Для задания необходимых параметров оптимизации нажатием кнопки Параметры откроем окно Параметры поиска решения (рис.4). В этом окне оставьте неизменными установленные по умолчанию Максимальное время: 100 сек, выделяемое на поиск решения (возможно до 9 часов), Предельное число итераций: 100, Относительная погрешность: 0,000001, Допустимое отклонение: 5%, переключатели в положении линейная, прямые, Ньютона. Установим флажок Линейная, чтобы обеспечить применение симплекс-метода, и нажмите кнопку ОК. 2. В окне Поиск решения нажмите кнопку Выполнить. На экране появится диалоговое окно Результаты поиска решения (рис.5) с информацией «Решение найдено. Все ограничения и условия оптимизации выполнены», подтверждающей успешное решение задачи оптимального распределения ресурсов и количественные результаты (значения переменных, ограничений и целевой функции), приведенные на рис.6. x1 = А3 = 0, x2 = В3 = 14,43, x3 =С3 = 39,93, x4 =D3 =15,10, x5 =Е3=0 При этом значение целевой функции: L= В5 = -144,99. 3.1.4. Анализ оптимального решения Анализ оптимального решения начинается после успешного решения задачи, когда на экране появляется диалоговое окно Результаты поиска решения. С его помощью можно подготовить три типа отчетов: по результатам (опция Результаты), по устойчивости (опция Устойчивость), по пределам (опция Пределы). 1. Подготовим отчет по результатам (рис.7). Отчет состоит из трех таблиц. В первой таблице (Целевая ячейка) приводятся сведения о целевой функции: исходное значение (в графе «Исходно») и оптимальный результат (в графе «Результат»). Во второй таблице (Изменяемые ячейки) приводятся исходные (в графе «Исходно») и полученные в результате решения задачи (в графе «Результат») значения переменных x1, x2, x3, x4, x5. Третья таблица (Ограничения) отображает результаты оптимального решения, касающиеся ограничений и граничных условий. 2. Щелчком на ярлычке Отчет по устойчивости откроем содержимое отчета на рабочем листе (рис. 8). Отчет по устойчивости содержит две таблицы. В первой таблице (Изменяемые ячейки) приводятся следующие значения переменных: результаты решения задачи (графа «Результ. значение»); нормированная стоимость, т.е. дополнительные двойственные переменные vj, 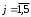 , которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение; , которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение;коэффициенты целевой функции (графа «Целевой коэффициент»); предельные значения приращения коэффициентов cj целевой функции (последние две графы), при которых сохраняется набор переменных, входящих в оптимальное решение. Во второй таблице приводятся значения ограничений: значения используемых (графа «Результ. Значение») и заданных (графа «Ограничение, правая часть») ресурсов; теневая цена, т. е. двойственные оценки zi, которые показывают, как изменится целевая функция при изменении ресурсов на единицу; значения приращения ресурсов Δbi (последние две графы), при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение. 3. Отчёт по переделам (рис.9) показывает, в каких пределах может меняться выпуск продукции, вошедшей в оптимальное решение, при сохранении его структуры: приводятся значения хi в оптимальном решении (графа «Значение»); даются нижние и верхние пределы изменения хi и соответствующие значения целевой функции (в графах «Целевой результат»). 3.2. Решение одноиндексной задачи линейного программирования |
