Линейное программирование. Задачи линейного программирования
 Скачать 89.93 Kb. Скачать 89.93 Kb.
|
|
3.2.1. Построение модели В данной задаче искомыми неизвестными являются количество полок каждого вида, которые будут произведены в текущем месяце. Таким образом, Х1 – количество полок А(шт./мес.); Х2 – количество полок В1(шт./мес.); Х3 – количество полок В2(шт./мес.). Целевая функция: Прибыль определяется разностью между ценой и себестоимостью, тогда:  L(х) = (192-150)х1+(154-120)х2+(147-134)х3 мах L(х) = (192-150)х1+(154-120)х2+(147-134)х3 махРуб./шт.* шт./мес. =руб./мес. Ограничения: Ограничения по фонду времени ( с использованием трудоемкости работ) 3,2 х1  27*8*1*22 27*8*1*22ч/шт.* шт./мес.  чел.* ч/(чел.см.)*см./дн. * дн./мес. чел.* ч/(чел.см.)*см./дн. * дн./мес.ч/мес.  ч/мес. ч/мес.3,2 ч/шт. (Тр1) – это время, затрачиваемое на столярные работы при производстве одной полки типа А; 27 чел. (Р1) – это количество столяров; 8ч/(чел.*см) – количество часов работы 1 человека в течении смены; 1см./дн. – количество смен в одном рабочем дне; 22 дн./мес. – количество рабочих дней в месяце Необходимо произвести проверку единиц измерения! Аналогично – упаковочные работы: 6/60х1+9/60х2+10/60х3  7,4*8*1*22 7,4*8*1*22ч/мес.  ч/мес ч/мес7 чел. (Р2) – это количество упаковщиков Ограничение по фонду времени на покрытие лаком полок типа А: 1/2*х1  7,4*1*22 7,4*1*22ч/шт.*шт./мес.  ч/см.*см./дн.*дн./мес. ч/см.*см./дн.*дн./мес.ч/мес.  ч/мес. ч/мес.1/2 – коэффициент, показывающий количество часов, приходящихся на покрытие лаком одной полки типа А. Автомат работает в смену 7,4 ч в смену (ФВ1). Ограничение по фонду времени на резку стекла для полок типа А и В2: 2/180х1+2/180х3  7,1*1*22 7,1*1*22ч/шт.*шт./мес.  ч/см.*см./дн.*дн./мес. ч/см.*см./дн.*дн./мес.ч/мес.  ч/мес. ч/мес.Ограничения по фонду времени на производство комплектующих полок типа В1 и В2: 1/7х2+1/7х3  7,8*1*22 7,8*1*22ч/шт.*шт./мес.  ч/см.*см./дн.*дн./мес. ч/см.*см./дн.*дн./мес.ч/мес.  ч/мес. ч/мес.Ограничения по запасу расходуемых в производстве материалов (по запасу используемых для производства полок деталей).. Целесообразно ориентироваться не на количество листов ДСП, а на количество комплектов для полок, которые можно получить из имеющегося запаса ДСП. Поскольку листы ДСП можно раскраивает различными способами и получать при этом различное количество деталей и комплектов, то обозначим месячный запас комплектов в правой части как Yкомпл и рассмотрим способ его численного определения позже. 1х2+1х3  Yкомпл YкомплКомпл./шт.*шт./мес.  Компл./мес. Компл./мес.Компл./мес.  Компл./мес. Компл./мес.Аналогично составляем ограничения по запасу задних стенок из ДВП для полок В1, В2: 1х2+1х3  215*6 215*6Задняя стенка/шт.*шт./мес.  лист ДВП/мес.*задняя стенка/лист ДВП лист ДВП/мес.*задняя стенка/лист ДВПЗадняя стенка/мес.  Задняя стенка/мес. Задняя стенка/мес.Где 215 – ежемесячный запас листов ДВП 6 – количество задних стенок полок из каждого листа ДВП. Ограничения по запасу стекол для полок А и В2: 2х1+2х3  240*13 240*13стекло/шт.*шт./мес.  лист стекла /мес.*стекло /лист стекла лист стекла /мес.*стекло /лист стекластекло/мес.  стекло/мес. стекло/мес.Где 240 – ежемесячный запас стекол 13 – количество стекол из каждого листа стекла. Ограничения по емкости вспомогательных помещений и рынка. Ограничение по количеству полок А, которые может вместить сушилка: х1  55*22 55*22шт./мес.  шт./дн.*дн./мес. шт./дн.*дн./мес.шт./мес.  шт./мес. шт./мес.где 55 – количество полок, которые могут быть просушены в течение месяца. Ограничение на количество полок всех видов, которые может вместить склад готовой продукции: х1+х2+х3  370-80+72*22 370-80+72*22шт./мес.  шт./мес.-шт./мес.+шт./дн.*дн./мес. шт./мес.-шт./мес.+шт./дн.*дн./мес.шт./мес.  шт./мес. шт./мес. Здесь учитывается, что общая емкость склада уменьшается на остаток полок, которые остались невывезенными с прошлого месяца. Кроме того, в течение месяца каждый день будет освобождаться по N мест для полок. Ограничение по примерной емкости рынка: х1+х2+х3  1100 1100шт./мес.  шт./мес. шт./мес.1100 – емкость рынка по всем видам полок. Ограничение по гарантированному заказу. х1  5, 5,х3  12 12шт./мес.  шт./мес. шт./мес.Необходимо произвести как минимум 5 полок А и 12 полок В3. Ограничения по соотношению объемов продаж различных товаров. Процентное отношение количество полок А и В1 ко всему объему продаж: (х1-5)+х2  0,43[(х1-5)+х2+(х3-12)] 0,43[(х1-5)+х2+(х3-12)]0,57х1+0,57х2-0,43х3 - 2,31 Шт./мес.  шт./мес. шт./мес.Определение количества комплектов для полок В1 и В2 3.2.2. Первый этап решения задачи В зависимости от размеров листов ДСП и габаритов полок детали В1 и В2 можно выкроить различными способами. Рассмотрим 3 возможных варианта такого раскроя (рис.10). L  (Y)=Yкомпл мах комппл./мес. (Y)=Yкомпл мах комппл./мес.Согласно 1 варианту из одного листа ДСП для полок В1 и В2 можно выкроить 19 деталей верхней и нижней стенок, а также 9 деталей боковых стенок. По 2 варианту раскроя получаем 12 деталей верхней и нижней стенок и 36 деталей боковых стенок. По 3 варианту раскроя получаем 16 деталей верхней или нижней стенок и 18 деталей боковых стенок. Обозначим количество листов ДСП, раскроенных в течение месяца : по 1-му варранту через у1(лист./мес.); по 2 варианту – у2(лист./мес.); по 3 варианту – у3(лист./мес.). Таким образом, наша цель – укомплектовка максимального количества полок – описывается целевой функцией:  L(Y)=Yкомпл мах L(Y)=Yкомпл махКоличество всех раскроенных листов ДСП не должно превышать 415, то есть ежемесячный запас их на складе: у1+у2+у3  415 415лист./мес. Количество верхних и нижних стенок, получаемых при раскрои: 19у1+12у2+16у3  2Yкомпл 2Yкомплдет,мес.  дет./мес. дет./мес.Ограничение, задающие нижнюю границу количества боковых стенок полок: 9у1+36у2+18у3  2Yкомпл 2Yкомплдет,мес.  дет./мес. дет./мес.Получаем модель задачи, позволяющую раскроить максимальное количество комплектов:  L(Y)=Yкомпл мах L(Y)=Yкомпл мах у1+у2+у3 у1+у2+у3 415 41519у1+12у2+16у3  2Yкомпл 2Yкомпл9у1+36у2+18у3  2Yкомпл 2Yкомплу1,у2,у3,Yкомпл  0 0Решим данную задачу с помощью функции Поиск решения в MS Excel. Для этого повторим все пункты выполнения работы 3.1.2 – 3.1.3 (рис.11). 3.2.3. Решение исходной одноиндексной задачи Решив задачу для варианта 0 мы получил значение правой части ограничения Y = 3515 комплектов, после чего решаем исходную задачу, модель которой имеет следующий вид:   L(х) = 42х1+34х2+13х3 мах L(х) = 42х1+34х2+13х3 мах3,2х1  4752; 4752;0,1х1+0,15х2+0,167х3  1232; 1232;0,5х1  162,8; 162,8;0,011х1+0,011х3  156,2; 156,2;0,143х2+0,143х3  171,6; 171,6;х2+х3  3515; 3515;х2+х3  1290; 1290;2х1+2х3  3120; 3120;х1  1210; 1210;х1+х2+х3  1874; 1874;х1+х2+х3  1100; 1100;х1  5; 5;х3  12; 12;0,57х1+0.57х2+0,43х3  -2,31; -2,31;х1,х2,х3  0 0Решим задачу с использованием функции Поиск решения в MS Excel аналогично пунктам 3.1.2-3.1.3. В ячейку Е5 введем целевую функцию, в ячейки В6:В19 – ограничения, переменные будем изменять в ячейках В3:В5 (рис.12). Решив задачу, получаем: х1=326шт./мес., х2=762 шт./мес., х3 = 12 шт./мес., L(X) = 39753 руб./мес., т.е. в текущем месяце необходимо произвести 326 полок А, 762 полки В1, 12 полок В2. После реализации всех произведенных полок комбинат получит прибыль в размере 39753 рублей. Оформим отчеты аналогично п.3.1.4. Отчет по результатам, состоящий из 3 таблиц: Информация о целевой функции. Информация о значениях переменных, полученных в результате решения задачи. Результаты оптимального решения для ограничений и для граничных условий. Анализ отчета показывает, что мы можем уменьшить фонд времени фонд времени по производству полок В на 60,86 ч и это никак не повлияет на оптимальное решение. Таким образом, мы снизим время работы автомата, производящего комплектующие полки В1 и В2. Емкость сушилки может быть снижена до 326 полок. На основании проведенного анализа можно сделать вывод о том, что существуют причины, не позволяющие мебельному комбинату выпускать большее количество полок и получать большую прибыль. Проанализировать эти причины позволяет отчет по устойчивости. Отчет по устойчивости Проанализировав 2 таблицу, мы увидим, что целесообразно увеличить емкость рынка самое большое на 425,6 = 426 полок. Это приведет к новым оптимальным решениям, увеличивающим прибыль по сравнению с найденной. Дальнейшее увеличение емкости рынка сверх указанных пределов не будет больше улучшать решение. Из колонки «Теневая цена» видно, что каждая полка, которая будет размещена на рынке, принесет прибыль равную 34 руб.. Отчет по пределам показывает найденные результаты и пределы, в которых они могут изменяться. 3.3. Решение двухиндексной задачи линейного программирования. Транспортная задача 3.3.1. Определение переменных Обозначим через хij [меш.] количество мешков с мукой, которые будут перевезены с i-го склада в j-ю хлебопекарню. 3.3.2. Проверка сбалансированности задачи Прежде чем проверять сбалансированность задачи, надо исключить объем гарантированной поставки из дальнейшего рассмотрения. Для этого вычтем 40 т из следующих величин: из запаса третьего склада = 60-40= 20т/мес.; из потребности в муке пятой хлебопекарни b2 = 73,92-40 = 33,92 т/мес. Согласно условию задачи мука хранится и перевозится в мешках по 50 кг, то есть единицами измерения переменных хij являются мешки муки. Но запасы муки на складах и потребности в ней магазинов заданы в тоннах. Поэтому для проверки баланса и дальнейшего решения задачи приведем эти величины к одной единице измерения - мешкам. Например, запас муки на первом складе равен 80 т-мес., или 80т/мес. / 0,050т./меш.= 1600 меш/мес, а потребность третьей хлебопекарни составляет 58,88т/мес, или 58,88т/мес / 0,050 т./меш.= 1178меш./мес. Округление при расчете потребностей надо проводить в большую сторону, иначе потребность в муке не будет удовлетворена полностью. Для данной ТЗ имеет место соотношение склады хлебопекарни 1600+1400+400+1100 < 1178+1249+679 4500меш./мес. 3106 меш./мес. Ежемесячный суммарный запас муки на складах больше суммарной потребности хлебопекарен на 1394 мешков муки, откуда следует вывод: ТЗ не сбалансирована. 3.3.3. Построение сбалансированной транспортной матрицы Сбалансированная транспортная матрица представлена в таблице 3. Стоимость перевозки муки должна быть отнесена к единице продукции, то есть к 1 мешку муки. Так, например, тариф перевозки из первого склада в третий магазин равен 800 руб./т • 0,050 т/меш. = 40 руб./меш. Для установления баланса необходим дополнительный фиктивный магазин. Фиктивные тарифы перевозки зададим таким образом, чтобы они были дороже реальных тарифов. Невозможность доставки грузов с третьего склада в третью хлебопекарню и с четвертого склада в пятую хлебопекарню задается в модели с помощью запрещающего тарифа, который должен превышать величину фиктивного тарифа. Таблица 3 Транспортная матрица задачи
3.3.4. Задание целевой функции Формальная ЦФ, то есть суммарные затраты на все возможные перевозки муки, учитываемые в модели, задается следующим выражением: L(X) = 40 х11+10х12 + 10х13 +50 х14 + +25х21+30х22 +25х23+50 х24+ + 100х31 + 30х32 +15х33 +50 х34+  +10 х41+20 х42 +100 х43+50 х44 min (руб./мес).. +10 х41+20 х42 +100 х43+50 х44 min (руб./мес).. При этом следует учитывать, что вследствие использования фиктивных тарифов реальная ЦФ будет меньше формальной ЦФ на стоимость найденных в процессе решения фиктивных перевозок. Задание ограничений: х11+х12 + х13 + х14 =1600,  х21+х22 +х23+ х24 =1400, х21+х22 +х23+ х24 =1400,х31 + х32 +х33 + х34=400, х41+ х42 + х43+ х44 =1100, х11+ х21+ х31 + х41=1178, х12+х22+ х32+ х42=1249, х13+х23+х33+ х43=679, х14+ х24+ х34+ х44 =1394, хij  0( 0(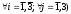 . .Решим задачу с помощью средств MS Excel. Аналогично пунктам 3.1.2-3.1.3-введем данные, целевую функцию в ячейку F3, ограничения - в ячейки С8:С15 (рис.16). Стоимость фиктивных перевозок составит: 127410 руб.. Найдем стоимость необходимых перевозок: 127410-1400(сумма фиктивных расходов)= 126010 руб. Из рис.13 мы также видим какое количество мешков муки из какого склада поступит на каждую хлебопекарню: 2х3 = 1178 мешка; 1х4 = 1027 мешка; 2х4 = 222 мешка; 1х5 = 573 мешка + гарантированная поставка 800 мешков; 4х5 = 106 мешков (перевозка запрещена). Заключение После проведенных вычислений, в первой задаче, на нахождение значения переменных, обеспечивающие минимизацию целевой функции, мы получили следующие результаты: x1 = А3 = 0, x2 = В3 = 14,43, x3 =С3 = 39,93, x4 =D3 =15,10, x5 =Е3=0 Во втором решении, одноиндексной задачи линейного программирования, получаем итоговый ответ: х1 = 326шт./мес., х2 = 762 шт./мес., х3 = 12 шт./мес., L(X) = 39753 руб./мес., В транспортной задаче, номер 3, стоимость необходимых перевозок составила 126010 руб. В данной работе мы не только исследовали, но и доказали выгодность проведения расчетов задач линейного программирования и, в частности, электронных таблиц Excel. Библиографический список 1. А.Н. Карасев, Н.Ш. Кремер, Т.Н. Савельева [текст]: «Математические методы в экономике», 1996. – 354 с. 2. Общий курс высшей математики для экономистов [Текст]: Учебник / под ред В.И. Ермакова.- М.: ИНФА - М. - 656 с. - (серия «высшее образование»). 3. Т.Л. Партыкина, И.И. Попов Математические методы [Текст]: учебник. - М.: ФОРУМ: ИНФА-М, 2005. - 464 с.: ил - (профессиональное образование). 4. Федосеев В.В. и др. Экономико-математические методы и прикладные модели: учебное пособие для ВУЗов. - М.: Юнити, 2002. 5. Лященко И.Н. Линейное и нелинейное программирования [Текст]: И.Н.Лященко, Е.А.Карагодова, Н.В.Черникова. - К.: «Высшая школа», 1992, 372 с. 6. Гольштейн Е.Г., Юдин Д.Б. Задачи линейного программирования транспортного типа. - M.: Наука, 1989. - 382с. 7. Балашевич В.А. [Текст]: Основы математического программирования. Мн.: Выш. шк. 2002. - 173с. 8. Branch M.A., T.F. Coleman, Y. Li. [Текст]: A Subspace, Interior, and Conjugate Gradient Method for Large-Scale Bound-Constrained Minimization Problems. SIAM Journal on Scientific Computing, Vol. 21, Number 1, pp. 1-23, 1999. | |||||||||||||||||||||||||||||||||||||||||

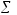 = 4500
= 4500