Лабораторная физическая установка. Курсач. Курсовой проект тема Лабораторная физическая установка Учебная дисциплина Проектирование и моделирование физических установок
 Скачать 6.9 Mb. Скачать 6.9 Mb.
|
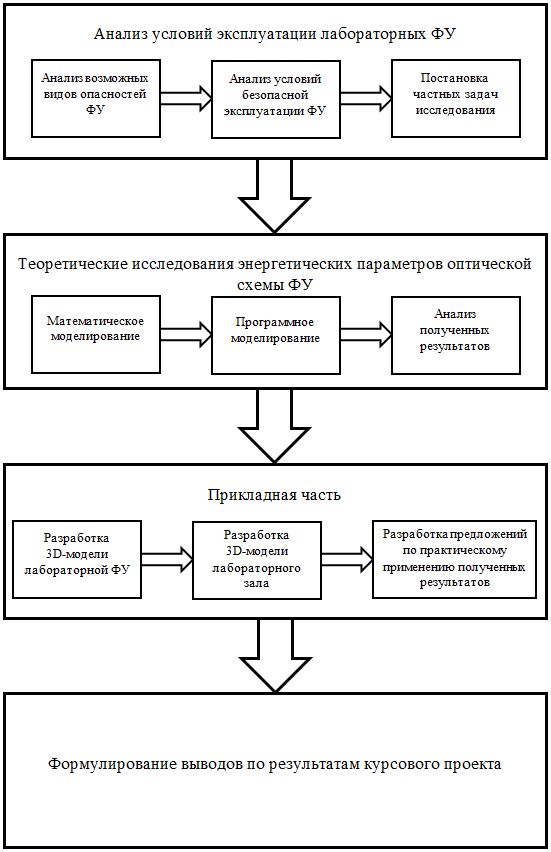
1.3 Постановка частных задач исследованияДля достижения цели курсового проекта – улучшения качества подготовки инженеров и научных сотрудников – необходимо решить, помимо основной, следующие частные задачи: разработать математическую модель функционирования лабораторной ФУ; разработать программную модель функционирования лабораторной ФУ; разработать предложения по практическому применению результатов проектирования. Математическая модель функционирования лабораторной ФУ необходима для обеспечения возможности количественного расчета проводимых исследований, а также для обоснования необходимости использования применяемых оптических элементов. Программная модель функционирования лабораторной ФУ необходима для автоматизации и ускорения проводимых математических вычислений для конкретной оптической схемы. Предложения по практическому применению необходимы для закрепления полученных результатов в практике и обеспечения возможности внедрения их в научную и образовательную практику. Таким образом, решение поставленных частных задач позволит достичь цели исследования, структура которого показана на рисунке 1.3
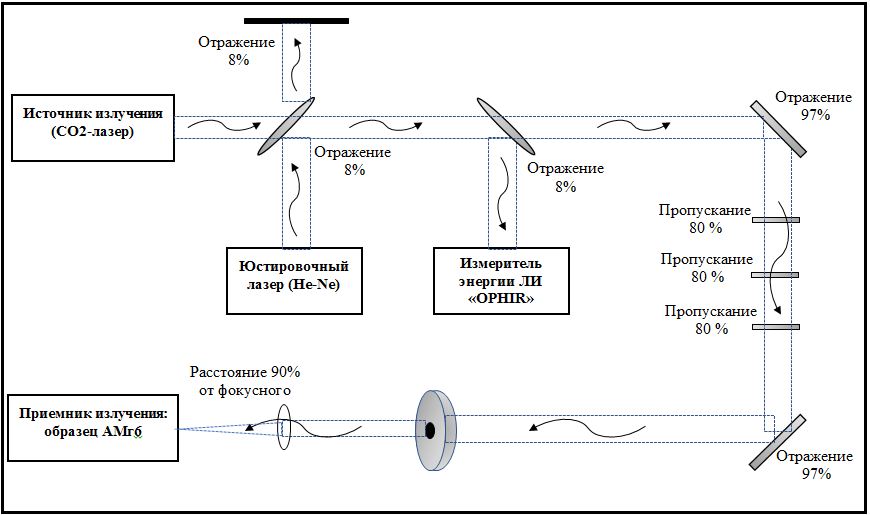
2 ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ ПАРАМЕТРОВ ЛАБОРАТОРНЫХ ФИЗИЧЕСКИХ УСТАНОВОК2.1 Математическое моделирование функционирования лабораторных физических установокДля обеспечения возможности качественного и количественного исследования энергетических характеристик ЛИ на элементах оптической схемы ФУ на базе СО2-лазера была разработана математическая модель функционирования ФУ. Моделирование проведено с использованием системы автоматизированного проектирования Mathcad [7], позволяющего выполнять и анализировать важнейшие расчеты с заданной точностью, применительно к лабораторной ФУ, оптическая схема которой показана на рисунке 2.1
Из рисунка 2.1 видно, что ФУ генерирует ЛИ, на которое после прохождения первого плоскопараллельного оптического окна накладывается излучение красного спектра юстировочного He-Ne лазера (в целях настройки и подсветки оптической трассы). При попадании ЛИ на второе окно часть его отражается и попадает на измеритель энергетических параметров типа «OPHIR». Оставшаяся часть излучения отражается от 2-х алюминиевых зеркал и, при необходимости, ослабляется с помощью германиевых оптических фильтров [8]. После чего отразившаяся часть излучения проходит диафрагму, фокусирующую линзу и попадает на приемник ЛИ (лабораторный образец). Содержание математической модели функционирования лабораторной ФУ дальнего Ик-диапазона составляют аналитические зависимости, ограничения и допущения. К числу задач математического моделирования лазерно-физических процессов относится задача определения энергетических параметров излучения ФУ на лабораторном образце, а также на элементах оптической схемы, и, кроме того, определение конечной температуры образца при воздействии ЛИ. Расчет энергетических характеристик ЛИ на элементах оптической схемы ФУ на базе СО2-лазера, а также тепловой характеристики образца из АМг6 [9] проведен по следующим формулам: Расчет энергии ЛИ, дошедшей до измерителя типа «OPHIR» (преобразования позволят с достаточной точностью определить начальное значение энергии ЛИ):
Расчет энергии ЛИ, отразившегося от первого оптического зеркала:
Расчет энергии ЛИ, прошедшего 3 оптических фильтра:
Расчет энергии ЛИ, отразившегося от второго оптического зеркала:
Расчет энергии ЛИ, прошедшего диафрагму:
Расчет радиуса облучения после линзы:
Расчет плотности мощности ЛИ на образце:
Расчет температуропроводности:
Расчет длины теплопроводности:
Расчет глубины поглощения излучения материалом:
Расчет конечной температуры образца:
Вариант исходных данных и соответствующие результаты расчетов приведены в таблице 2.1. Таблица 2.1 Исходные данные и результаты расчетов
Из данных таблицы 2.1 видно, что ФУ на основе СО2-лазера с начальной энергией 7.7 Дж при точечной фокусировке (при помощи диафрагмы и собирающей линзы) при длительности импульса 0,7 мс обеспечивает создание на поверхности лабораторного образца плотность мощности ЛИ ≈ 1,43ГВт/м2, что позволяет достичь на поверхности материала (АМг6) температуры порядка 3150 К. Данные условия позволяют испарять материал (Tисп = 2500К) на достаточно малой площади, что может быть полезно при прецизионной обработке. Расчеты проведены с использованием программы Mathcad, скриншот рабочего окна показан на рисунке 2.2
В математической модели ввиду использования оценочного характера и в целях упрощения расчетов были приняты следующие допущения: излучение падает перпендикулярно поверхности образца и входной апертуры измерителя; сечение лазерного пучка круглое; энергия по сечению лазерного пучка и во времени распределена равномерно; показатель поглощения излучения в линзе пренебрежимо мал; свойства материала изотропны и не зависят от температуры. Постановка задачи математического моделирования удовлетворяет требованиям пункта 2.2.15 Национального стандарта РФ «Численное моделирование физических процессов» [12]. Таким образом, разработанная математическая модель функционирования лабораторных ФУ дальнего ИК-диапазона (на базе СО2-лазера) обеспечивает возможность проведения количественной и качественной оценки энергетических характеристик ФУ при использовании их по назначению и получение корректных результатов, а также создание вариативности оценок для выбора наиболее энергетически выгодного варианта путем изменения количества оптических фильтров и радиуса диафрагмы (пункты 3, 5 рисунка 2.2) при неизменных значениях начальной энергии и длительности импульса. Помимо этого, математическая модель позволяет оценить конечную температуру образца при воздействии по нему лазерного излучения (при условии импульсного режима обручения и поверхностного поглощения). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

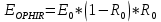 ,
,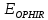 – энергия ЛИ, дошедшая до измерителя типа «OPHIR», Дж;
– энергия ЛИ, дошедшая до измерителя типа «OPHIR», Дж;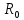 – коэффициент отражения плоскопараллельного окна;
– коэффициент отражения плоскопараллельного окна;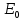 – начальная энергия ЛИ.
– начальная энергия ЛИ.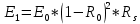 ,
,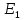 - энергия ЛИ, отразившегося от первого оптического зеркала, Дж;
- энергия ЛИ, отразившегося от первого оптического зеркала, Дж;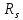 - коэффициент отражения оптического зеркала.
- коэффициент отражения оптического зеркала.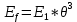 ,
,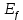 - энергия ЛИ, прошедшего 3 оптических фильтра, Дж;
- энергия ЛИ, прошедшего 3 оптических фильтра, Дж;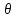 – коэффициент пропускания оптического фильтра.
– коэффициент пропускания оптического фильтра.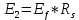 ,
,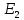 - энергия ЛИ,
- энергия ЛИ, 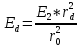 ,
,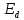 - энергия ЛИ, прошедшего диафрагму, Дж;
- энергия ЛИ, прошедшего диафрагму, Дж;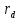 – радиус диафрагмы, м;
– радиус диафрагмы, м;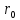 – радиус облучения (до диафрагмы), м.
– радиус облучения (до диафрагмы), м.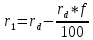 ,
,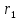 – радиус облучения после линзы, м;
– радиус облучения после линзы, м;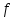 – размещение образца, процент от фокусного расстояния линзы.
– размещение образца, процент от фокусного расстояния линзы.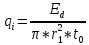 ,
,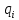 - плотность мощности ЛИ на образце, Вт/м2;
- плотность мощности ЛИ на образце, Вт/м2;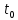 – продолжительность облучения, с.
– продолжительность облучения, с.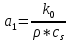 ,
,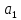 – температуропроводность образца, м2/с;
– температуропроводность образца, м2/с;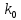 – коэффициент теплопроводности образца, Вт/(м*К);
– коэффициент теплопроводности образца, Вт/(м*К);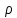 – плотность образца, кг/м3;
– плотность образца, кг/м3;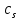 – удельная теплоемкость образца, Дж/(кг*К).
– удельная теплоемкость образца, Дж/(кг*К).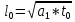 ,
,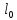 –
– 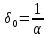 ,
,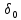 – глубина поглощения излучения материалом, м;
– глубина поглощения излучения материалом, м;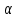 – показатель поглощения излучения образцом, м-1.
– показатель поглощения излучения образцом, м-1.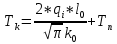 [10],
[10],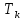 – конечная температура образца, К;
– конечная температура образца, К;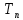 – начальная температура образца, К.
– начальная температура образца, К.