Краткосрочный план
|
|
Раздел 8.3А: Квадратичная функция
|
Школа:
|
Дата:
|
ФИО учителя:
|
Класс: 8
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Квадратичная функция и ее график
|
Урок №2 серии из 9 уроков
|
|
Тип урока
|
Урок закрепления знаний и навыков
|
Цели обучения (ссылка на учебную программу)
|
8.4.1.2 знать свойства и строить графики квадратичных функций вида y = a(x – m)2, y = ax2 + n , y = a(x – m)2 + n, a≠0
|
Цели урока
|
Строить графики квадратичных функций, заданных различным способом.
Выполнять преобразования графиков функции.
|
Критерии оценивания
|
Навыки
|
Критерий оценивания
|
Знание и понимание
|
знает этапы построения графиков функций вида y = a(x – m)2, y = ax2 + n , y = a(x – m)2 + n, a≠0
|
Применение знаний
|
выполняет преобразования графиков функции
|
|
Языковые цели
|
Учащиеся устно перечисляют основные этапы и шаги построения графика квадратичной функции.
Предметная лексика и терминология
− квадратичная функция;
− парабола;
− параллельный перенос;
− симметричное отображение графика;
− сжатие к оси х;
− сжатие вдоль оси у;
− растяжение от оси х;
− растяжение вдоль оси у;
− сдвиг вверх, сдвиг вниз;
− сдвиг вправо, сдвиг влево.
Серия полезных фраз для диалога/письма
− график данной функции можно получить из графика функции… с помощью двух параллельных переносов: сдвига на … единиц … (вправо, влево) вдоль оси х и сдвига на … единиц (вверх, вниз) вдоль оси у;
− график функции у = kf(х) при k>1 получается из графика функции y = f(x) – растяжением от оси х в k раз;
график функции у = kf(х) при 0<k< 1 получается из графика функции y = f(x) – сжатием к оси х в  раз. раз.
|
Привитие ценностей
|
Уважение, сотрудничество, открытость.
Привитие ценностей осуществляется через деятельность учащихся на уроке.
|
Межпредметные связи
|
Решение задач по геометрии, физике
|
Навыки использования ИКТ
|
Презентация, построение графиков в программеDesmos или GeoGebra
|
Предварительные знания
|
Учащиеся знают, как построить графики функций вида y = a(x – m)2, y = ax2 + n.
|
Ход урока
|
Этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Начало урока
1мин
7 мин
|
Организационный момент
Постановка целей урока.
Актуализация знаний
Работа в парах
Учащиеся в парах выполняют разные задания, затем сверяются с учащимися других пар, исправляют ошибки при их наличии. Затем учащиеся в своих парах объясняют друг другу решения своих заданий. На слайде представлены фразы, которые учащиеся могут использовать во время обсуждения.
№1
В одной системе координат постройте графики функций:
а) 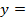 x2 x2
б) 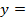 x2- 3 x2- 3
в) 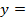 1 + x2 1 + x2
№2
В одной системе координат постройте графики функций:
а) 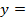 - x2 - x2
б) 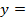 - (x - 2)2 - (x - 2)2
в) 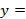 - (x + 4)2 - (x + 4)2
|
Презентация
Слайды 1-2
Приложение 1
Слайд 3
|
Середина урока
8 мин
13 мин
5 мин
|
Изучение нового материала
Рассмотреть построение графика функции вида y = a(x – m)2 + n, например, y = 3(x – 1)2 + 2. После обсуждения этапов построения и выполнения построения на слайде демонстрируется алгоритм.
Индивидуальная работа
Самостоятельное построение графиков функций:
1. 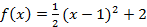 ; ;
2. 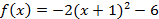 ; ;
3. 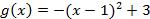 ; ;
4. 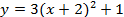
После окончания работы учащиеся проверяют правильность построений с помощью программ DesmosилиGeoGebra.
Работа в группах
Задание на сопоставление графиков функций и формул, задающих эти функции. Каждая группа получает набор карточек и работает сообща. Последняя из карточек с формулами является лишней. Ученики должны будут отложить ее либо можно предложить им изобразить схематически график этой функции. Также можно убрать одну из формул и предложить учащимся самостоятельно составить ее.
Задание для формативного оценивания
Уровень А.
№ 1. Постройте график функции y=2(x-5)2+1, запишите все этапы построения.
№2. Запишите формулу задающую функцию, которая получится при перемещении графика функции у= 2х2на 2 единицы влево и на 3 единицы вниз.
Уровень В.
№ 1. Постройте график функции y=-0,5(х+2)2-1, запишите все этапы построения.
№2. Запишите формулу задающую функцию, которая получится при перемещении графика функции у= -2х2на 3,1 единицы влево и на 8 единиц вниз. Схематично изобразите график этой функции.
|
Слайд 4
Приложение 2
Ноутбуки с установленной программой Desmosили GeoGebra
Приложение 2
Приложение 3
|
Конец урока
2 мин
|
Рефлексия
Учащиеся становятся в круг. Учитель бросает мяч одному из учеников и просит ответить на один из вопросов:
Что тебе понравилось в уроке?
Что было интересным?
Каике новые знания ты получил?
Был ли ты успешным на уроке?
Какие трудности ты испытывал в течение урока?
Какие вопросы остались нерешенными?
Домашнее задание
1. Постройте график функции:
а) 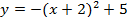 ; ;
б) 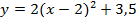 ; ;
в) 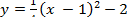 . .
2. Выделите квадрат двучлена из квадратного трехчлена:
а) 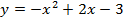 ; ;
б) 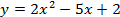 . .
|
Слайд 5
Приложение 2
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
|
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
|
Здоровье и соблюдение техники безопасности
|
Дифференциация выражена в подборе заданий,учащимся будут предложены задания стандартного уровня, а также более сложные задания, требующие мыслительных навыков высокого порядка.
|
Во время актуализации знаний будет использовано взаимооценивание для улучшения прогресса учащихся. Учащиеся используют математические программы для самопроверки и устранения ошибок.
|
Учащиеся будут менять виды деятельности для поддержания концентрации внимания и работоспособности.
|
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
|
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
|
|
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
1:
2:
Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?
1:
2:
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|
 Скачать 52.07 Kb.
Скачать 52.07 Kb.