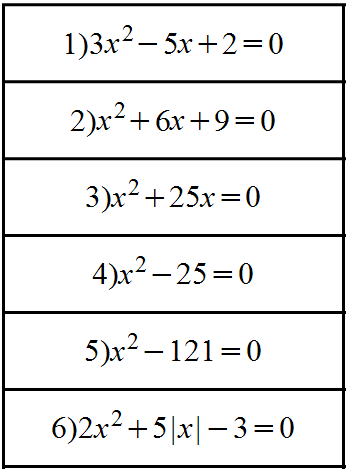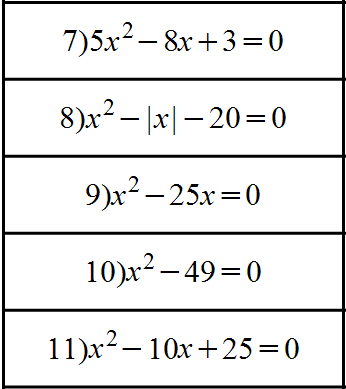Раздел долгосрочного плана:
Повторение курса алгебры 8 класса
|
|
Дата:
|
Ф.И.О. учителя:
|
Класс:9
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Квадратные и дробно-рациональные уравнения.
|
Тип урока
|
Повторение изученного
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
|
8.2.2.3 решать квадратные уравнения;
8.2.2.4 применять теорему Виета;
8.2.2.5 решать уравнения вида |ax2+bx|+c=0; ax2+b|x|+c=0;
8.2.2.6 решать дробно-рациональные уравнения.
|
Цели урока
|
Повторить алгоритмы решения квадратных уравнений; квадратных уравнений, содержащих знак модуля и уметь решать их.
|
Критерии оценивания
|
различает виды квадратного уравнения;
знает формулы дискриминанта, корней квадратного уравнения;
знает и применяет алгоритм решения квадратных уравнений, в том числе неполных квадратных уравнений;
знает и применяет алгоритм решения дробно-рационального уравнения;
приводит уравнения вида ax2+b|x|+c=0 к квадратным;
отбирает корни, соответствующие требуемым условиям.
|
Языковые цели
|
Учащиеся рассуждают о выборе способа решения квадратного уравнения.
Предметная лексика и терминология
Уравнение, модуль, значение переменной, значение выражения
Серия полезных фраз для диалога/письма
Рассмотрим два случая для значения числа / выражения …
Выполним проверку корней
|
Привитие ценностей
|
Сотрудничество через различные виды деятельности учащихся на уроке.
|
Межпредметные связи
|
Умение составлять и решать уравнения необходимо учащимся при изучении различных дисциплин.
|
Навыки использования ИКТ
|
|
Предварительные знания
|
Виды квадратных уравнений.
|
Ход урока
|
Запланированные этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Начало урока
5 мин
15 мин
|
Приветствие учащихся.
Задание1. Обобщите.
Ознакомить учащихся с темой и целями урока.
Работа в парах.
Задание 2. Разделите уравнения на группы.
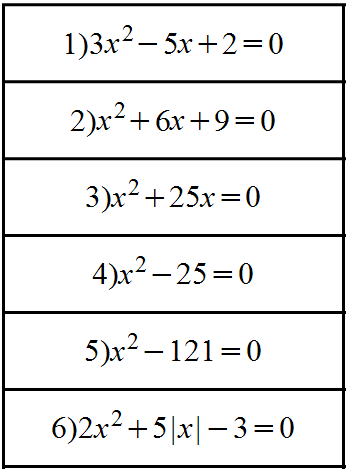 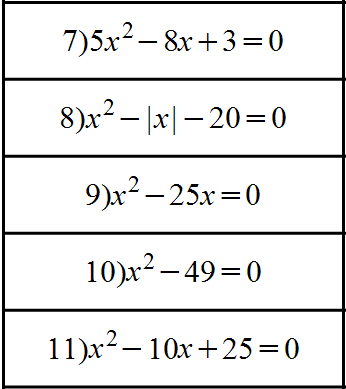
Обсудить с учащимися их принципы разделение уравнений на группы.
Предполагаемые группы:
Группа 1-2. Неполные кв.уравнения. (3, 9; 4, 5, 10)
Группа 3-4. Кв.уравнения (1, 7)
Приведенные кв.уравнения (2, 11)
Группа 5. Кв.уравнения, содержащие знак модуля ( 6, 8)
Работа в группах. Создание и защита постера. Решение квадратных уравнений.
Цель: повторить и обобщить знания по решению квадратных уравнений различных видов.
Разработка критериев оценивания работы совместно с учащимися. Например:
- указан вид уравнения,
- описан алгоритм решения уравнения в общем виде,
- приведен пример решения уравнения,
- защита постера (выступление четкое, последовательное, понятное).
Создание постера.
Защита постера.
Группа 1. Решение неполного квадратного уравнения вида
ax2+ bx = 0; ax2+ c = 0.
Группа 2. Решение квадратного уравнения видаax2+ bx + c = 0.
Группа 3. Решение квадратного уравнения вида
ax2+ b| x |+ c = 0.
Алгоритм решения уравнения вида ax2+b|x|+c=0
Ввести замену t=|x|.
Учитывая, что x2=|x|2, решить уравнение at2+bt+c=0.
Решить уравнения t=|x| при t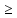 0. 0.
Напомнить учащимся о применении свойств коэффициентов при решении квадратных уравнений
ax2 + bx + c = 0:
Если a + b + c = 0 (сумма коэффициентов), то x1 = 1, x2 = c/a;
Еслиa – b + c = 0 илиb= a + c, тоx1 = –1, x2 = – c/a.
Взаимооценивание групп по разработанным критериям.
|
Презентация
Повторение_КвУр
Слайд 1
Слайд 2
Слайд 3
Слайд 4
Слайд 5
|
Середина урока
15мин
2 мин
|
Работа в группах. Решение квадратных уравнений
Цель: оценить уровень знаний и умений решать квадратные уравнения применять теорему Виета.
3, 9; 4, 5, 10
1, 7
2, 11
6, 8
Проверка с помощью Тарсии-домино.
Группа А – Приложение 1. (Некоторые из решеных уравнений + другие и должно получиться имя Франсуа Виет).
Группа В – Приложение 2.
Повторить теорему Виета, организовать проверку корней с помощью теоремы Виета.
ФО Самооценивание
Обобщить результаты работы, повторить способы решения квадратных уравнений.
|
Приложение 1
Тарсия. КвУр_домино_ГрА_Виет
Приложение 2
Тарсия. КвУр_домино_ГрВ
|
Конец урока
3 мин
|
Домашнее задание.
Решите уравнения:
а) 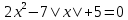
b) 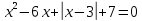
2. Упростите:
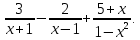
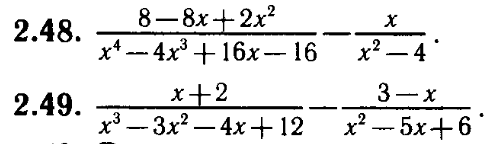
Подведение итогов
Самооценивание.
Знал…
Узнал…
Необходимо закрепить ...
|
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
|
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
|
Здоровье и соблюдение техники безопасности
|
Все учащиеся решают квадратные уравнения вида ax2+bx+c=0,
Большинство учащихся успешно решают уравнения вида ax2+b|x|+c=0 в простых случаях.
Некоторые учащиеся смогут решать сложные уравнения, например, содержащие знак модуля и выделение полного квадрата.
|
Взаимооценивание защиты постеров по предварительно разработанным учащимися критериям оценивания;
Самопроверка и самооценивание по результатам игры «Домино» - Тарсия;
Формативное оценивание учителем на протяжении всего урока.
|
Учащимся будут предложены разные виды деятельности для уменьшения нагрузки.
Презентация используется только вначале урока.
|
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
|
Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.
|
|
Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
1:
2:
Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?
1:
2:
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
|
 Скачать 63.59 Kb.
Скачать 63.59 Kb.