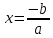Этапы урока
|
Деятельность учителя
|
Деятельность учащихся
|
УУД
|
Задания для участников
(на доске)
|
1.Организационный момент 1 мин
(проверка готовности обучающихся их эмоционального настроя на работу, включение в деятельность на личностно значимом уровне )
Итог: настрой на работу
|
Обеспечивает благоприятный настрой.
-Здравствуйте, ребята! Математику не зря называют «Царицей наук». Одно из замечательных свойств математики – любознательность. Давайте постараемся сегодня проявить свою любознательность на уроке.
|
-приветствие учителя;
-полная готовность к уроку;
-настрой на работу;
-организация внимания;
-оценивают готовность к уроку.
|
Самостоятельно формулировать познавательные цели, умение ориентироваться в своей системе знаний.
|
|
2. Актуализация опорных знаний урока. 5мин
Проверка опорных знаний учащихся, необходимых для изучения нового материала. Выявление типичных ошибок и пробелов в ЗУН для дальнейшей коррекционной работы
Итог: определение степени усвоения учащимися материала
|
Выполните задания.
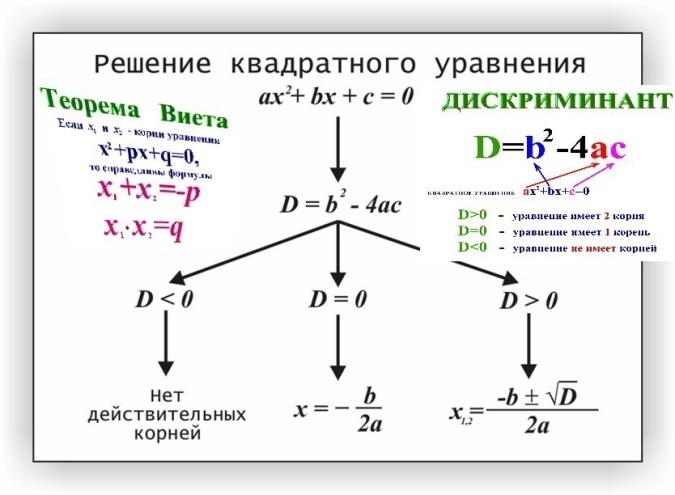
- Вспомним правила. Какими способами можно решить данные уравнения.
Правильно через дискриминант и с помощью теоремы Виета.
Посмотрите на слайд1. Решим данные уравнения 2 способами (по группам).
|
Выполняют задания по ранее пройденному материалу.
Проговаривают правила.
|
Личностные (самоопределение) Регулятивные (соотнесение того, что уже усвоено и известно)
|
1)Решите уравнения:
x2 + 4х - 5 = 0
x2- 2x - 3=0
|
3. Выход на запись темы урока.
Объяснение нового знания с постановки вопросов, выявлением проблемы. 4 мин
|
- Перед вами несколько уравнений. Попробуйте разделить данные уравнения по внешнему виду на группы.
- Чем различаются уравнения в этих группах?
|
Выбирают по порядку уравнения в группы.
|
Познавательные (анализ с целью выделения признаков объектов, подведение под понятие)
|
1) 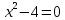
2) 4x2 - 16=0
3) 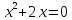
4) x2 = 81;
5) 4x2 = 0;
6) 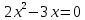
7) 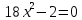
8) 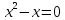
9) 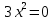
10) 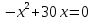
11) 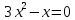
12) -5x2 = 0;
|
4.Формулирование проблемы.
2 мин
|
- Как можно назвать такие уравнения?
- Попробуйте сформулировать определение неполных квадратных уравнений.
- Как же будем решать такие уравнения?
- Все неполные уравнения можно разбить на три группы. По какому принципу?
- Верно. Наша задача найти способы решения этих уравнений.
|
Предлагают свои варианты… НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ.
- Если в квадратном уравнении хотя бы один из коэффициентов b или c равны 0, или оба равны 0, то такие уравнения называются неполными квадратными.
- Такие уравнения мы решать не умеем.
- Группы, где b =0, где c=0
и где b=0 и c=0
|
Познавательные (формулирование проблемы, самостоятельное создание способов решения проблем творческого и поискового характера)
|
|
5.Материал для выдвижения гипотез.
5 мин
|
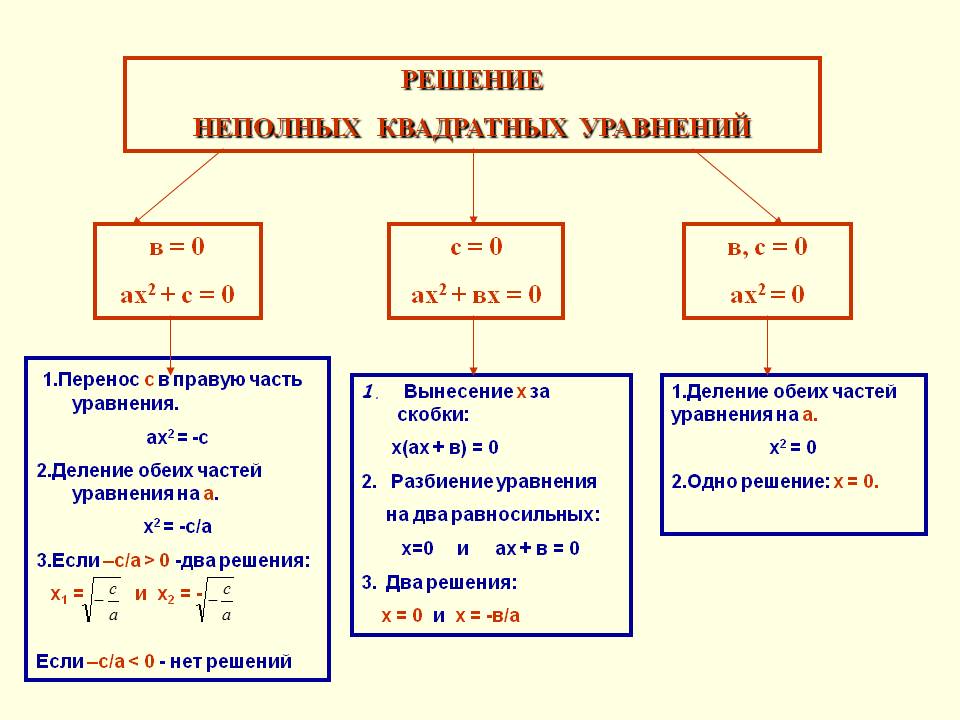
- Все неполные квадратные уравнения разобьем на три группы.
- Сейчас, разбившись на три группы, будем решать уравнения.
- Как можно решить уравнения? Ваши гипотезы?
(контролирует работу групп)
|
Учащиеся разделили и записали на доске.
Учащиеся работают в группах, решают в тетрадях.
|
Познавательные
Регулятивные (определение последовательности промежуточных целей, составление плана, прогнозирование)
|
I. 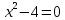
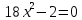
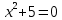
II.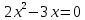
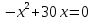
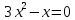
III.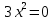
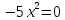
|
6.Представление гипотез группами.
5 мин
|
- Группы решите уравнения с помощью своей гипотезы и прокомментируйте.
1-я группа
- Ребята обобщите все вышесказанное.
- 2-я группа
- Ребята обобщите все вышесказанное.
- 3-я группа
|
- Переносим число в правую часть. Такие уравнения мы уже решали. Оно имеет два корня.
- остальные решаем аналогично.
- Уравнение вида
ax2+ c=0, где х – переменная, a, c – числа, с≠0 называется неполным квадратным и решается 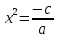
Если 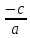 > 0, то имеем два корня > 0, то имеем два корня 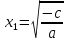 и и 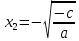 . .
Если 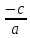 <0, то уравнение корней не имеет. <0, то уравнение корней не имеет.
- Вынесем х за скобки. Произведение двух множителей равно 0, если один или второй множитель равен 0.
- Уравнение вида
ax2+ bx=0, где х – переменная, a, b– числа, b≠0 называется неполным квадратным и решается x(ax+b)=0,
x=0 или 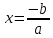
-Уравнение вида ax2=0, где х – переменная, a≠0 называется неполным квадратным и имеет единственное решение x=0.
|
Познавательные (выдвижение гипотез и их обоснование, построение логической цепи рассуждений)
Коммуникативные
Регулятивные (контроль и коррекция)
|
|
7.Работа с учебником.
5 мин
|
- Откроем учебник на странице 117-118 и сравним свои выводы.
Знакомит учащихся с понятием инфографика (вернемся к слайду1)
Попробуем сами составить инфографику для решения неполных квадратных уравнений (работа в группах)

|
Самостоятельно читают учебник, сверяют свои формулировки с формулировкой учебника, сверяют получившиеся инфографики с образцом.
|
Познавательные
|
|
8.Применение нового знания (контроль).
10 мин
|
- А сейчас закрепим полученные знания на практике, выполним самостоятельную работу.
https://urls.uchi.ru/l/117d7b
|
Решают в тетрадях.
|
Регулятивные (контроль и коррекция)
Познавательные (выбор эффективного способа
решения)
Коммуникативные
|
|
9.Домашнее задание
1 мин
|
https://urls.uchi.ru/l/ec2683
|
Обсуждение трудных этапов выполнения задания.
|
Регулятивные (целеполагание, контроль, оценка, коррекция)
|
|
10.Итог урока. Рефлексия деятельности.
2 мин
|
- Какую проблему мы сегодня с вами решали?
- Что нового узнали?
- Еще раз сформулируем эти правила.
- Что вам особенно понравилось на уроке?
- Есть ли вопросы?
На возникшие вопросы учитель отвечает.
- Итак, мы сегодня очень плодотворно поработали, давайте подведём итоги. Подсчитайте ваши баллы, заработанные на уроке, переведите их в оценку, согласно критериям.
- Какую оценку каждый из вас поставил бы себе за урок? Учитель выставляет оценки и объясняет за что.
-Всем спасибо за урок. Урок закончен.
|
- Изучили определение квадратного уравнения, познакомились с неполными квадратными уравнениями и способами их решения.
Формулируют.
Отвечают.
Ребята записывают оценки в своих листах.
|
Коммуникативные (умение выражать свои мысли)
Регулятивные (контроль, оценка, коррекция)
|
|
 Скачать 276.66 Kb.
Скачать 276.66 Kb.

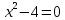
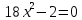
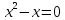
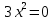
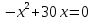
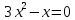
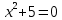
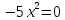
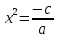
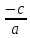 > 0, то имеем два корня
> 0, то имеем два корня 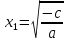 и
и 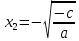 .
.