Определение объёма ствола срубленного дерева и его части разными способами. L длина ствола или его части, м
 Скачать 53.02 Kb.
|
|
Работа 2. Определение объёма ствола срубленного дерева и его части разными способами Определение объема ствола или его частей по простой формуле срединного сечения. Используют формулу 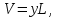 где V- объем ствола или его части, м3; у - площадь поперечного сечения на половине длины, м2; L - длина ствола или его части, м. Следовательно, вся задача сводится к нахождению на половине длины ствола или бревна площади поперечного сечения, которая определяется как площадь круга по диаметру на этой длине. В нашем примере длина ствола 20,8 м, половина длины 10,4 м, а диаметры на половине длины составляют в коре 16,1 см, без коры 15,5 см (см. табл. 1). Этим диаметрам соответствуют площади сечении: в коре 0,0204 м2, без коры 0,0189 м2. Подставляя в формулу объема полученные значения площадей сечений и длины, вычисляем объем: в коре V= 0,0204*20,8 = 0,424 м3; без коры V= 0,0189*20,8 = 0,393 м3. Результаты вычислений заносят в табл. 3. Таблица 3
Определение объема ствола или его частей по простой формуле среднего сечения. При этом находится полусумма площадей нижнего и верхнего сечений, которая затем умножается на длину ствола или бревна: 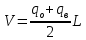 где q0 - площадь нижнего (толстого) сечения, м2; qв - площадь верхнего (тонкого) сечения, м2. Рассмотренная формула может быть использована только для определения объема части ствола. Для всего ствола она дает очень большое завышение (до 60 %). Площадь верхнего сечения ствола равна нулю, следовательно, объем ствола равен половине площади нижнего сечения, умноженной на длину: 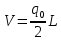 Результаты вычислений заносят в табл. 4. Таблица 4
Определение объема ствола по сложной формуле срединного сечения. Древесный ствол разделяют на равные по длине секции, чаще всего двух- или однометровые (в нашем примере длина секции принята 2 м). На середине каждой секции измеряют диаметры в коре и без коры. Объем секций можно вычислить по простой формуле срединного сечения, следовательно, объем всего ствола равен сумме объемов всех двухметровых секций плюс объем вершинки. Так как длина секции (l) одинакова, формулу можно записать как V=(у1+у2+y3+...+yn) l + Vn где у1,у2,y3,...,yn - площади срединных сечений секций (отрубков), м2; l - длина секций, м; Vв - объем вершины, м3. Таким образом, для нахождения объема ствола (без объема вершинки) этим способом нужно найти сумму площадей сечений на серединах двухметровых секций и умножить ее на длину секции. Схема вычислений и результаты расчетов приведены в табл. 5. Таблица 5
Полученные значения сумм площадей сечений умножают на длину секции (2 м) и получают объем всех секций: в коре 0,220*2 = 0,440 м3; без коры 0,191*2=0,382м3. Чаще ствол не делится точно на двухметровые секции, и остается вершина размером менее 2 м (в нашем примере длина вершины 1,8 м). Объем оставшейся вершины находят по формуле конуса: 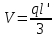 где q - площадь основания вершины, м2; 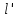 - длина вершины, м. Вычисленные объемы прибавляют к объему секций и получают объемы всего ствола: в коре 0,440+0,004 = 0,444 м3; без коры 0,382+ 0,004 = 0,386 м3. Способ определения объема вершин ствола по сложной формуле срединного сечения является наиболее точным из всех имеющихся способов с применением стереометрических формул. Точность этой формулы 3-4 %. Сравнение результатов вычислений объема ствола и полученные расхождения приведены в табл. 6. Таблица 6
Определение объема круглых лесных материалов (сортиментов). Для получения круглых лесных материалов древесный ствол разделяют на части - сортименты длиной 3; 3,5; 4; 4,5; 5; 5,5; 6 и 6,5 м, то есть любые из перечисленных размеров и в любом сочетании. Прежде всего устанавливается длина ствола, подлежащая распиловке, так как минимальный диаметр в верхнем (тонком) отрубе сортимента без коры должен быть более 7 см. В нашем примере деловая часть составляет 17 м, так как максимальная высота, на которой диаметр без коры более 7 см, равна17 м. Из этих 17м, например, можно выпилить пять сортимента: первый длиной 6, второй 4, третий 4, четвертый 3, пятый 3 м от основания ствола, и при этом остается еще вершина 3,8 м (рис. 1). 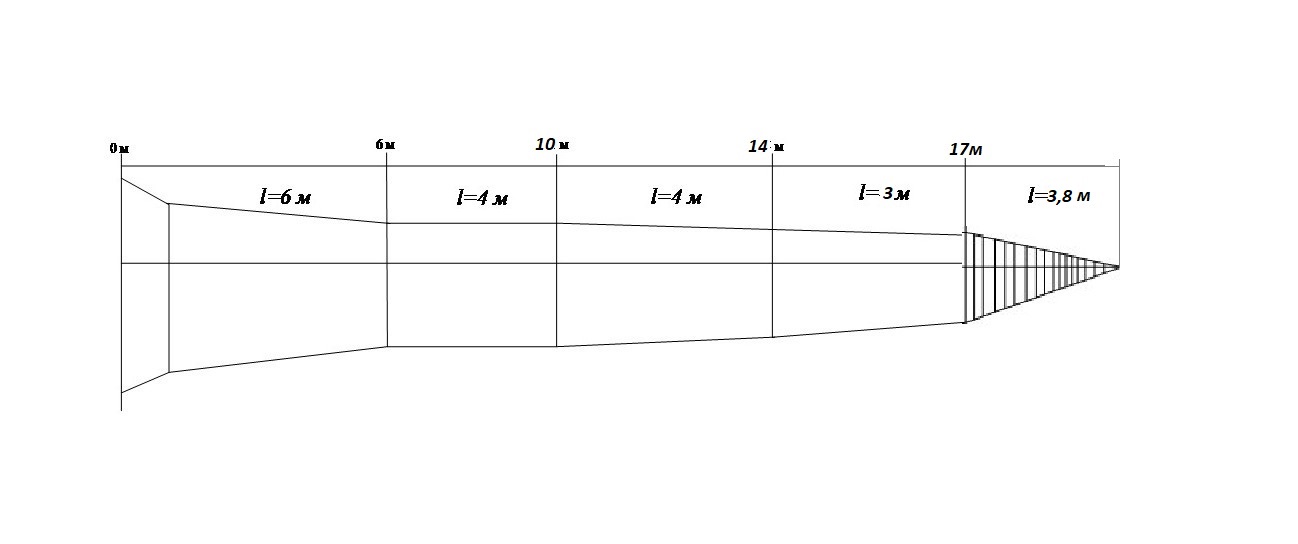 Рис. 1. Схема распиловки древесного ствола на сортименты Для вычисления объема сортиментов необходимо иметь значение диаметра или на середине длины сортимента, или в верхнем сечении (табл. 7). Для этого используют исходные данные контрольного задания 1. При необходимости следует применять метод интерполяции. Таблица 7
Сумма объемов отдельных круглых сортиментов, выпиленных из древесного ствола, дает объем ствола, но без объема вершинки. Объем вершин стволов определяется по таблице объемов вершин стволов, входами в которую являются диаметр основания (см) и длина вершины (м) (прил. 5). В нашем примере длина вершины 3,8 м; диаметры основания равны диаметрам верхнего сечения последнего сортимента (см. табл. 7) и составляют в коре 3,8 см, без коры 3,3 см. Объем вершины при этих данных: в коре 0,001 м3, без коры 0,001 м3. Прибавив к полученным объемам всех сортиментов объем вершин, получим объем всего ствола. Результаты сопоставления объемов ствола приведены в табл. 8. Таблица 8
Контрольные вопросы. Почему простую формулу среднего сечения нецелесообразно применять для определения объема целого ствола? Использование простой формулы срединного сечения для определения объема целых стволов дает систематическую ошибку в пределах от 5 до 25 %, поэтому, несмотря на свою простоту, эта формула не применяется для определения объема ствола дерева, но можно использовать ее для определения объема коротких отрезков ствола. Какие факторы влияют на точность вычисления объема по сложной формуле срединных сечений? Точность определения объема ствола по сложной формуле срединных сечений зависит от точностей замеров отрезка ствола: чем больше замеренных отрезков, тем больше точность результата. Как определяется объем круглых сортиментов, выпиленных из верхней части ствола? Определяется по таблице объемов вершин стволов, входами в которую являются диаметр основания (см) и длина вершины. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||