решение задач егэ. решение задач егэ планиметрия. Подготовка к егэ (база). Вариант 1 Основания трапеции равны 3 и Найдите отрезок, соединяющий середины диагоналей трапеции. 2
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
Подготовка к ЕГЭ (база). Вариант 1 1 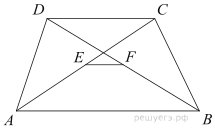 .Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции. .Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.  3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2 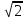 . .4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции. 5 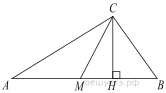 . Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах. . Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах. 6. Угол между хордой AB и касательной BC к окружности равен 35°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.  7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции. 8. Н  айдите величину угла АВС. Ответ дайте в градусах. айдите величину угла АВС. Ответ дайте в градусах.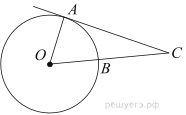 9. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах. 10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах. Подготовка к ЕГЭ (база). Вариант 2 В 1. Сторона правильного треугольника равна  Найдите радиус окружности, вписанной в этот треугольник. Найдите радиус окружности, вписанной в этот треугольник.2. Две стороны параллелограмма относятся как 9:11, а периметр его равен 40. Найдите большую сторону параллелограмма. 3. Н  айдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах. айдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах. 5  . Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника. . Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.6. Найдите радиус окружности, вписанной в треугольник 7  . Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника. . Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.8  . Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет. . Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции. 10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника. В  ариант 3 ариант 31. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах. 2. Н  айдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6. айдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6. 3. В треугольнике АВС АС = ВС = 4  , cos ВАС = 0,25. Найдите высоту АН. , cos ВАС = 0,25. Найдите высоту АН.4 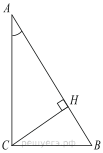 . В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах. . В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах.5. В треугольнике АВС угол С равен 90°, СН – высота, АС = 3, cos А =  . Найдите ВН. . Найдите ВН.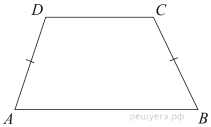 6  . Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции. . Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите 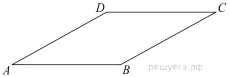 8. Найдите площадь ромба, если его диагонали равны 4 и 12. 9. В 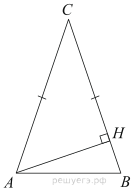 треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН. треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН. 10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах В  ариант 4 Планиметрия ариант 4 Планиметрия1. В треугольнике ABC угол C равен 90°, CH — высота, АВ = 15, tg А = 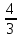 . Найдите BH. . Найдите BH.2. У  гол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах. гол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах. 3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба. 4.О  стрые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах. стрые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.5 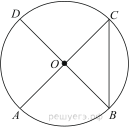 . У . У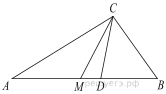 гол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника. гол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.  7  . Катеты равнобедренного прямоугольного треугольника равны 82 + 41 . Катеты равнобедренного прямоугольного треугольника равны 82 + 41 Найдите радиус окружности, вписанной в этот треугольник. 8  . В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах. . В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.9  . В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4 . В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4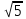 , ВН = 4. Найдите , ВН = 4. Найдите 10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника. Вариант 5 Планиметрия  1  . Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2 . Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2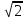 . .2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.  3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А =  . Найдите АН. . Найдите АН.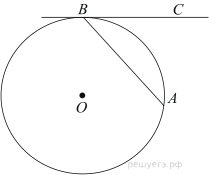 4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.  5. Катеты равнобедренного прямоугольного треугольника равны 2+  Найдите радиус окружности, вписанной в этот треугольник. Найдите радиус окружности, вписанной в этот треугольник. 6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции. 7   . Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ. . Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.8 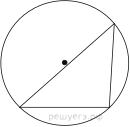 .Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах. .Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах. 10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма. В 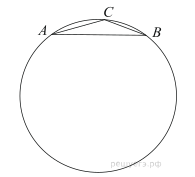 ариант 6 6. Планиметрия ариант 6 6. Планиметрия1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.  2  . Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах. . Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.3. В треугольнике АВС АС=ВС, АН – высота, АВ=5, sinВАС=  . Найдите . Найдите  4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.  5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.  6  . Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен . Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 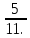 Найдите высоту трапеции. Найдите высоту трапеции.7. В треугольнике ABC угол C равен 90°, АС = 8, cos А =  Найдите АВ. Найдите АВ. 8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника. 9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма. 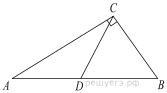 10. В треугольнике ABC угол ACB равен Вариант 7 6. Планиметрия 1   . Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах. . Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.2. Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.  3. В треугольнике ABC AC = BC, AB = 22, tg А =  . Найдите AC. . Найдите AC. 4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.  5. В треугольнике ABC угол C равен 90°, АС = 17, sin А =  . Найдите BC. . Найдите BC.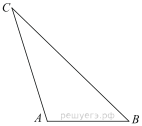 6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.  7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.  8. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.  9  . Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах. . Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника. В  ариант 8 6. Планиметрия ариант 8 6. Планиметрия1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.  2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.  3. Найдите вписанный угол, опирающийся на дугу, которая составляет 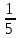 окружности. Ответ дайте в градусах. окружности. Ответ дайте в градусах. 4. В треугольнике ABC угол C равен 90°, АС = 17, sin А =  . Найдите BC. . Найдите BC.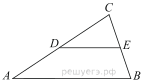 5. Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.  6. В треугольнике ABC AC = BC, AB = 8, tg А =  . Найдите AC. . Найдите AC. 7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах. 8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE. 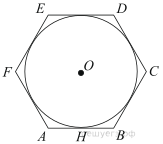 9  . Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47 . Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47 . .10. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2  В  ариант 9 6. Планиметрия ариант 9 6. Планиметрия1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. 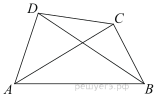 2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. 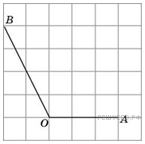 3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 4. Н  айдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах. айдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах. 5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.  6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС =  , Найдите высоту , Найдите высоту  7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n. 8  . Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB. . Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.9. Найдите вписанный угол, опирающийся на дугу, которая составляет 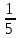 окружности. Ответ дайте в градусах. окружности. Ответ дайте в градусах. 10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла. В  ариант 10 6. Планиметрия ариант 10 6. Планиметрия1. Найдите величину угла АВС. Ответ дайте в градусах.  2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах. 3. Площадь треугольника АВС равна 129. ДE – средняя линия, параллельная стороне АВ. Найдите площадь трапеции АВЕД.  4. В треугольнике АВС угол С равен 90°, СН – высота, АН = 12 , cos А =  . Найдите АВ. . Найдите АВ. 5. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника. 6. О 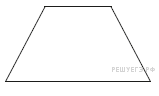 снования равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции. снования равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции. 7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°. 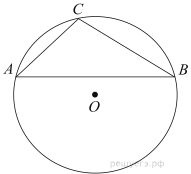 8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах. 9. В треугольнике  10. В треугольнике АВС АС = ВС = 27 ,  . Найдите . Найдите
| |||||||||||||||
