Курсовая - копия. Контрольные вопросы. Лаба 1 1

• Название: Лаба 1 1
• Анкор: Курсовая - копия.dox
• Дата: 23.05.2021
• Размер: 186.21 Kb.
• Имя файла: Контрольные вопросы .docx
• Тип: Документы; #208746

Лаба №1

1. При любых условиях в рабочем состоянии он является источником и того и другого (Без нагрузки это ток утечки. ) .
 Когда вращается генератор, на его выводах образуется ЭДС-напряжение. Если нагрузить выводы любым сопративлением, потечёт ток.
 Внутренне сопротивление =0 :генератор напряжения. И противно = бесконечности - генератор тока. Чему учат или хотят ли учится? Это учил в 75 году и помню. И все Ваши вопросы последующие - в ТОЭ описаны.
 холостой ход - источник напряжения (почти идеальный источник ЭДС)
короткое замыкание - источник тока.

2. Эквивалентным называется преобразование, при котором напряжения и токи в частях схемы, не подвергшихся преобразованию, не меняются.

3.

4. Согласованным режимом, в общем смысле, называется такой режим работы электрической цепи, когда на нагрузке, подключенной к данному источнику, выделяется максимальная мощность, которую способен дать этот источник в текущем его состоянии. Выходное сопротивление генератора равно сопротивлению нагрузки, при этом мощность максимальна. в случае с длинной линией ещё и равно волновому сопротивлению линии, тогда нет отражений и отсутствуют стоячие волны, получается наибольший КПД.

5.

Лаба №2
1. 1)Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда. Однако при расчетах следует учитывать, что это правило применимо только в случае пренебрежимо малой емкости узла. В противном случае первое правило может нарушаться, что особенно заметно при высокочастотных токах.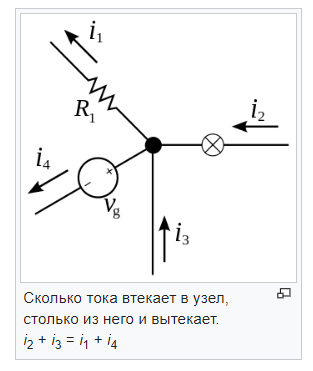



2) Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений {\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}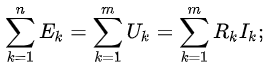

для переменных напряжений 

{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

2. По первому закону Кирхгофа можно составить столько уравнений, сколько узлов имеет электрическая цепь, т.е. у уравнений. Однако линейно независимыми будут только у - 1 уравнения. Покажем это на примере.

Составим уравнения по первому закону Кирхгофа для электрической схемы, у которой четыре узла и шесть ветвей (рис. 2.19).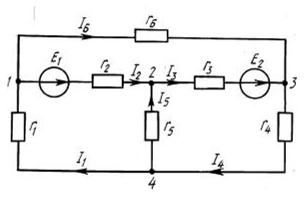



Р и с. 2.19

Произвольно выберем направления токов в ветвях; тогда для первого узла / — К — 4 = 0, для второго К + А — /3 = 0, для третьего /₆ + /₃ — /₄ = 0, для четвертого /₄ — /| — /₅ = 0. Сложив первые три уравнения, получим — /₄ + /| + /₅ = 0. Умножим это уравнение на — 1. Тогда уравнение для четвертого узла можно получить линейными комбинациями из уравнений, составленных по первому закону Кирхгофа для первых у — 1 узлов.

Видно, что одно из уравнений системы, составленное по числу узлов, является зависимым. Поэтому по первому закону Кирхгофа составляется только у — 1 уравнение, т.е. на одно меньше, чем число узлов в электрической цепи. Так как в схеме четыре узла, то число уравнений, которые составляются по первому закону Кирхгофа, равно трем. Остальные п = Ь — (у — 1) линейно независимых уравнений составляются по второму закону Кирхгофа. Для рассматриваемой схемы п = 6 — (4 — 1) = 3.

Таким образом, для электрической цепи, содержащей у узлов и Ь ветвей, по второму закону Кирхгофа можно составить п = Ь - (у - 1) линейно независимых уравнений. При этом общее число уравнений, составленных по первому и второму законам Кирхгофа, будет равно числу ветвей электрической цепи.

3. Принцип наложения формулируется следующим образом: ток (напряжение) на участке цепи, в которой действуют несколько независимых источников ЭДС и тока, равен алгебраической сумме токов (напряжений), вызываемых каждым из этих источников в отдельности. Принцип наложения является фундаментальным свойством линейных цепей: реакция линейной цепи при одновременном действии нескольких независимых источников равна сумме реакций, получающихся при действии каждого источника в отдельности

4. Метод наложения справедлив для линейных электрических цепей, основан на принципе независимости действия источников. Он состоит в определении и последующем суммировании, т.е. наложении частичных токов ветвей от действия каждого источника в отдельности (или группы источников). При определении частичных токов i-го источника все остальные идеальные источники ЭДС закорачиваются, а ветви с идеальными источниками тока разрываются.

Лаба №3

1. Гармоническим ( синусоидальным) током называется переменный ток, который с течением времени изменяется по закону синуса или косинуса:

i = I_m sin ( wt - j ),

или i = I_m cos ( wt - j ).

Здесь i - мгновенное значение переменного тока - величина тока, соответствующая данному моменту времени,

I_m - максимальное ( амплитудное ) значение тока,

(wt - j ) - фаза синусоидального тока,

w = 2pn - круговая ( циклическая ) частота тока,

n- частота тока,

j- начальная фаза.

Гармонический ток создается синусоидальным или косинусоидальным напряжением той же частоты:

u = U_m sinwt

u = U_m coswt.

2. 1) ПЕРИОДИЧЕСКИЕ КОЛЕБАНИЯ - колебания, при которых значения параметров колебательной системы, меняющихся во времени, в точности повторяются через равные промежутки времени.

2)  В соответствии с (2.7) действующее значение периодического тока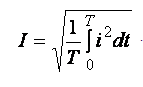

 . (2.8)

    Возведя (2.8) в квадрат и умножив обе части полученного выражения на RT, найдем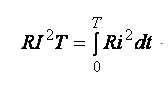

 .

    Это равенство показывает, что действующее значение периодического тока равно по величине такому постоянному току, который, проходя через неизменное сопротивление R, за период времени Т выделяет то же количество тепла, что и данный ток i.

    Аналогично действующее значение периодического напряжения

 . (2.9)

При токе i = Imcosωt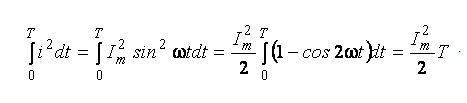

 .

Следовательно, согласно (2.8)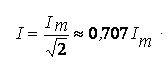

 . (2.8а)

Аналогично действующее значение гармонического напряжения

 . (2.9а)

    Номинальные токи и напряжения электротехнических устройств определяются, как правило, действующими значениями; поэтому действующие значения представляют наиболее распространенный электрический параметр.

3. 1)Сопративление: в резистивном элементе с сопротивлением R электромагнитная энергия преобразуется в тепловую при мощности преобразования  Резистивные элементы вводят в схему также и для учета необратимого преобразования электромагнитной энергии в другие формы энергии (например, в механическую) и для учета излучаемой энергии.

2) Индуктивность: Амплитуда и действующее значение напряжения и тока на индуктивности связаны законом Ома. Напряжение u_L опережает по фазе ток i_L на  .

Мгновенная мощность может быть положительной, отрицательной и равной нулю (рис. 3.6). Если p(t) 0, индуктивность заряжается энергией в виде энергии магнитного поля; если p(t) 0,индуктивность возвращает энергию источнику. Средняя мощность за период P_ср= 0(мгновенная мощность колеблется относительно нуля).

3) Емкость: Мгновенная мощность может быть положительной, отрицательной и равной нулю (рис. 3.8). Если p(t) 0, емкость заряжается энергией в виде энергии электрического поля; если p(t) 0, емкость возвращает энергию источнику. Средняя мощность за период P_ср = 0,а, следовательно, и активная мощность равна нулю, что означает, что происходит обмен энергией без потерь, емкость – реактивный элемент.

4. При активном сопротивление ток и напряжение совпадают по фазе (нет сдвига векторов) - при индуктивном ток отстаёт от напряжения на 90 градусов - при емкости ток опережает напряжение на 90 - при активно-индуктивном ток отстаёт от напряжения. на угол фи. зависящий от соотношения активного и индуктивного сопротивления, например. (из треугольника сопротивлений)

5. 1) Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты. Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений либо их амплитудных величин.
2) RLC: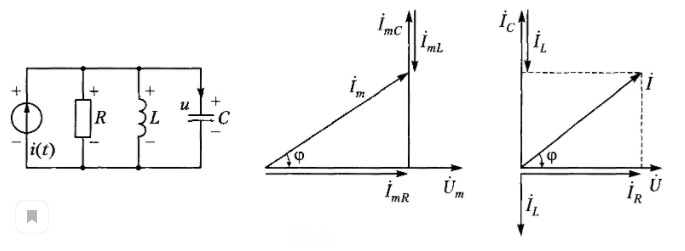

RС: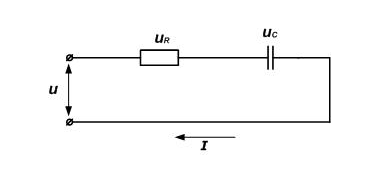

RL: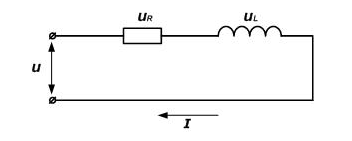

Лаба №4

1. Передаточная функция - один из способов математического описания динамической системы. Используется в основном в теории управления, связи, цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал. Передаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме.

2. 1) Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов.  АЧХ устройства определяется по зависимости коэффициента передачи (или коэффициента усиления) от частоты. ИЛИ Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства.

2) ФЧХ расшифровывается как фазо-частотная характеристика, phase response – фазовый отклик. Фазо-частотная характеристика – это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания. ИЛИ Фазо-частотная характеристика – это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

3. Степень искажения синусоидальных сигналов линиями связи оценивается с помо­щью таких характеристик, как амплитудно-частотная характеристика, полоса про­пускания и затухание на определенной частоте. Амплитудно-частотная характеристикапоказывает, как затухает ам­плитуда синусоиды на выходе линии связи по сравнению с амплитудой на ее входе для всех возможных частот передаваемого сигнала. Вместо амплитуды в этой ха­рактеристике часто используют также такой параметр сигнала, как его мощность.

4. Реакцию цепи на гармоническое воздействие определим с помощью анализа переходных процессов (Transient Analysis). Перед началом расчета переходных процессов рассчитывается режим по постоянному току. Шаг интегрирования выбирается автоматически. Анализируя полученный результат можно сделать вывод, что с изменением входного уровня сигнала коэффициент передачи фильтра изменяется при различных значениях R4. Чем больше сопротивление, тем больше глубина переходного процесса. Изменения наблюдаются при изменении R4 в пределах от 1 кОм до 50 кОм. Дальнейшие изменения управляющего сопротивления к изменению коэффициента передачи не приводят.

5.

Лаба №5

1. Это Резкое увеличение амплитуды колебаний при приближении частоты вынуждающей силы к собственной частоте колебаний системы.

2. 1) Явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям

2) Характеристическим сопротивлением последовательного /7Х'-коптура называется сопротивление реактивного элемента при резонансе. Оно обозначается р и согласно определению равно



3) Полоса пропускания частот, диапазон частот, в пределах которого амплитудно-частотная характеристика (АЧХ) акустического, радиотехнического или оптического устройства достаточно равномерна для того, чтобы обеспечить передачу сигнала без существенного искажения его формы.

4) Добротностью контураQ называется величина, показывающая, во сколько раз напряжение на индуктивности или емкости при резонансе превышает входное напряжение:



Лаба №6

1. Операторной передаточной функцией линейной электрической цепи К(р) называют отношение изображения выходной величины Х(р) к изображению входной величины F(p) при нулевых начальных условиях: По аналогии с комплексными передаточными функциями операторными передаточными функциями цепи, рассматриваемой как четырехполюсник, являются: передаточная функция по напряжению, по току.

2. 1) Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов.  АЧХ устройства определяется по зависимости коэффициента передачи (или коэффициента усиления) от частоты. ИЛИ Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства.

2) ФЧХ расшифровывается как фазо-частотная характеристика, phase response – фазовый отклик. Фазо-частотная характеристика – это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания. ИЛИ Фазо-частотная характеристика – это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.

3. Переходная характеристика цепи   – это отношение реакции этой цепи при нулевых начальных условиях к величине этого воздействия при нулевых начальных условиях. Переходная характеристика цепи (как и импульсная) относится к временным характеристикам цепи, т. е. выражает некоторый переходный процесс при заранее установленных воздействиях и начальных условиях.

Операторной передаточной функцией цепи называют - отношение изображения реакции к изображению входного воздействия. Функции цепи определяют при нулевых начальных условиях, поэтому в операторных схемах замещения индуктивного и емкостного элементов отсутствуют независимые источники.

4.Импульсная (весовая) характеристика или импульсная функция   цепи – это ее обобщенная характеристика, являющаяся временной функцией, численно равная реакции цепи на единичное импульсное воздействие на ее входе при нулевых начальных условиях, другими словами, это отклик цепи, свободной от начального запаса энергии на дельта-функцию Дирана   на ее входе. Импульсная и комплексная передаточные функции пассивной электрической цепи связаны между собой парой преобразования Фурье. А это, в свою очередь, означает, что импульсная характеристика однозначным образом определяет комплексную передаточную функцию цепи и наоборот. Причем, для h(t) и H(jw) справедливы все свойства и теоремы. Основные теоремы спектрального анализа. В частности, из теоремы изменения масштаба независимого переменного следует, что чем более растянута во времени импульсная характеристика цепи, тем уже ее АЧХ и наоборот. Условия безыскаженной передачи сигналов через линейную цепь было показано, что для неискажающей линейной цепи АЧХ должна быть равномерна, а это соответствует согласно импульсной характеристике цепи в виде d-функции, что полностью подтверждает изложенное.

5.

6. Временной и частотный методы анализа переходных процессов базируются на двух взаимосвязанных характеристиках электрических цепей: импульсной или переходной, с одной стороны, и комплексной передаточной функции, с другой. Между этими характеристиками существует однозначное соответствие. Определим эту связь. Допустим, что на вход пассивной электрической цепи с комплексной передаточной функцией H(jw) приложено воздействие в виде единичной импульсной функции. Тогда с учетом того, что спектр единичного импульсного сигнала равен единице, спектр выходного сигнала согласно будет:



Обратное преобразование определит выходной сигнал f₂(t), который численно равен импульсной характеристике цепи:



7. Полоса пропускания (bandwidth) — это непрерывный диапазон частот, для которого отношение амплитуды выходного сигнала ко входному превышает некоторый заранее заданный предел, обычно 0,5. То есть полоса пропускания определяет диапазон частот синусоидального сигнала, при которых этот сигнал передается по линии связи без значительных искажений.

8.

9.