1715-716 — корекція3. Лабораторна робота 1
 Скачать 1.63 Mb.
|
|
Лабораторна робота 4.1. Розробка програми швидкого дискретного потенціювання (ШДП) для виконання обчислювальних операцій в алгоритмі шифрування RSA. Лістинг програмного коду виконання завдання: using System; using System.IO; using System.Numerics; namespace LargeNumbersCalculator { class Adder { private static Random random = new Random(); private const int MinNumberOfDigits = 1000; private const int MaxNumberOfDigits = 10000; public static string SumValuesFromFiles(String path) { string[] lines = File.ReadAllLines(path); BigInteger firstNumber = BigInteger.Parse(lines[0]); BigInteger secondNumber = BigInteger.Parse(lines[1]); Console.WriteLine("\nПерше довге числ:\n"); Console.WriteLine(firstNumber); Console.WriteLine("\nДруге довге число:\n"); Console.WriteLine(secondNumber); return (firstNumber + secondNumber).ToString(); } public static string SumValuesFromFiles2(String path) { string[] lines = File.ReadAllLines(path); BigInteger firstNumber = BigInteger.Parse(lines[0]); BigInteger secondNumber = BigInteger.Parse(lines[1]); Console.WriteLine("\nПерше довге число:\n"); Console.WriteLine(firstNumber); Console.WriteLine("\nДруге довге число:\n"); Console.WriteLine(secondNumber); return (firstNumber - secondNumber).ToString(); } public static string SumValuesFromFiles3(String path) { string[] lines = File.ReadAllLines(path); BigInteger firstNumber = BigInteger.Parse(lines[0]); BigInteger secondNumber = BigInteger.Parse(lines[1]); Console.WriteLine("\nПерше довге число:\n"); Console.WriteLine(firstNumber); Console.WriteLine("\nДруге довге число:\n"); Console.WriteLine(secondNumber); return (firstNumber * secondNumber).ToString(); } public static string SumValuesFromFiles4(String path) { string[] lines = File.ReadAllLines(path); BigInteger firstNumber = BigInteger.Parse(lines[0]); BigInteger secondNumber = BigInteger.Parse(lines[1]); Console.WriteLine("\nПерше довге число:\n"); Console.WriteLine(firstNumber); Console.WriteLine("\nДруге довге число:\n"); Console.WriteLine(secondNumber); return (firstNumber / secondNumber).ToString(); } public static string SumGeneratedValues() { string firstString = GenerateLongValue(); string secondString = GenerateLongValue(); BigInteger firstNumber = BigInteger.Parse(firstString); BigInteger secondNumber = BigInteger.Parse(secondString); Console.WriteLine("\nПерше довге число:\n"); Console.WriteLine(firstString); Console.WriteLine("\nДруге довге число:\n"); Console.WriteLine(secondString); return (firstNumber + secondNumber).ToString(); } public static string GenerateLongValue() { int numberOfDigits = random.Next(MinNumberOfDigits, MaxNumberOfDigits); string generatedNumber = ""; for (int i = 0; i < numberOfDigits; i++) { generatedNumber += GenerateDigit(); } return generatedNumber; } public static string SumGeneratedValues2() { string firstString = GenerateLongValue(); string secondString = GenerateLongValue(); BigInteger firstNumber = BigInteger.Parse(firstString); BigInteger secondNumber = BigInteger.Parse(secondString); Console.WriteLine("\nПерше довге число:\n"); Console.WriteLine(firstString); Console.WriteLine("\nДруге довге число:\n"); Console.WriteLine(secondString); return (firstNumber - secondNumber).ToString(); } public static string SumGeneratedValues3() { string firstString = GenerateLongValue(); string secondString = GenerateLongValue(); BigInteger firstNumber = BigInteger.Parse(firstString); BigInteger secondNumber = BigInteger.Parse(secondString); Console.WriteLine("\nПерше довге число:\n"); Console.WriteLine(firstString); Console.WriteLine("\nДруге довге число:\n"); Console.WriteLine(secondString); return (firstNumber * secondNumber).ToString(); } public static string SumGeneratedValues4() { string firstString = GenerateLongValue(); string secondString = GenerateLongValue(); BigInteger firstNumber = BigInteger.Parse(firstString); Console.WriteLine("\nДовге число:\n"); Console.WriteLine(firstString); return (firstNumber * firstNumber).ToString(); } public static string SumGeneratedValues5() { string firstString = GenerateLongValue(); string secondString = GenerateLongValue(); BigInteger firstNumber = BigInteger.Parse(firstString); BigInteger secondNumber = BigInteger.Parse(secondString); Console.WriteLine("\nПерше довге число:\n"); Console.WriteLine(firstString); Console.WriteLine("\nДруге довге число:\n"); Console.WriteLine(secondString); return (firstNumber % secondNumber).ToString(); } public static string GenerateDigit() { return random.Next(0, 10).ToString(); } } } using System; using System.IO; namespace LargeNumbersCalculator { class Program { static void Main(string[] args) { //Console.WriteLine("\nSUMA:\n" + Adder.SumGeneratedValues()); Console.WriteLine("\nСУМА:\n" + Adder.SumValuesFromFiles(Path.Combine(Environment.CurrentDirectory, "числа.txt"))); Console.ReadKey(); Console.WriteLine("\nРIЗНИЦЯ:\n" + Adder.SumGeneratedValues2()); Console.ReadKey(); Console.WriteLine("\nДОБУТОК:\n" + Adder.SumGeneratedValues3()); Console.ReadKey(); Console.WriteLine("\nКВАДРАТ:\n" + Adder.SumGeneratedValues4()); Console.ReadKey(); Console.WriteLine("\nЗАЛИШКИ ПО МОДУЛЮ ДІЛЕННЯ ДВОХ ЧИСЕЛ:\n" + Adder.SumGeneratedValues5()); Console.ReadKey(); } } } Результат запуску програми на виконання:        Лабораторна робота 4.2. Розробка програми генератора великих простих чисел (ВПЧ). Метод решета числового поля (як спеціальний, і загальний) можна як удосконалення найпростішого методу — методу раціонального решета, чи методу квадратичного решета. Подібні до них алгоритми вимагають знаходження гладких чисел порядку  . Розмір цих чисел експоненційно зростає із зростанням . Метод решета числового поля, у свою чергу, вимагає знаходження гладких чисел субекспоненційного щодо розміру. Завдяки тому, що ці числа менші, ймовірність того, що число такого розміру виявиться гладким вище, що є причиною ефективності методу решета числового поля. Досягнення прискорення обчислень у межах методу проводять у числових полях, що ускладнює алгоритм, проти більш простим раціональним решетом.Основні принципи Метод факторизації Ферма для факторизації натуральних непарних чисел n, що полягає у пошуку таких цілих чисел x та y, що  , що веде до розкладання .Знаходження підмножини множини цілих чисел, добуток яких — квадрат Складання факторної бази: набору  де pi — прості числа такі, що для деякого B.Просіювання виконується подібно до решету Ератосфена (звідки метод і отримав свою назву). Решетом служать найпростіші числа факторної бази та їх ступеня. При просіюванні число не «викреслюються», а поділяється на число із решета. Якщо в результаті число виявилося одиницею, воно B-гладке. Основна ідея полягає в тому, щоб замість перебору чисел та перевірки, чи діляться їх квадрати по модулю n на прості числа з факторної бази, перебираються прості числа з бази та одразу для всіх чисел виду  перевіряється, чи діляться вони це просте число чи його ступінь.Обчислювальну складність алгоритмів модулярного експонентування за її реалізації різних обчислювальних платформах зазвичай оціните кількістю використаних них операцій процесорного множення. Процесорними називають цілі операції, що виконуються над k-розрядними числами, довжина яких відповідає розрядності процесора. Процес модулярного експоненцування зводиться до послідовного виконання log2E = n циклів, у кожному з яких виконується операція зведення в квадрат результату операції попереднього циклу і в залежності від поточного біта ступеня E виконується операція множення. Залежно від порядку, в якому аналізуються розряди ступеня E, можна розглянути 2 типи алгоритмів експоненцювання: 1) алгоритми, що передбачають аналіз розрядів ступеня Е, починаючи зі старших розрядів (зліва направо). У нотаціях мови програмування алгоритм цього може бути поданий як: 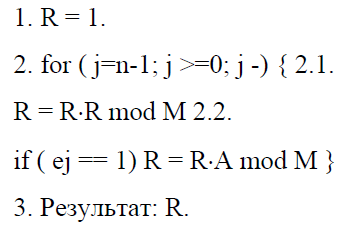 При цьому, під час кожної ітерації циклу виконується зведення числа квадрат і множення на постійне число, що дорівнює А, що створює потенційні передумови для підвищення швидкості множення. Недоліком є те, що операції виконуються строго послідовно та належать критичному шляху. Не дозволяє реалізувати паралельне обчислення операцій. 2) Алгоритми, які передбачають аналіз розрядів ступеня Е починаючи з молодших (праворуч ліворуч). Алгоритм модулярного експонентування цього може бути представлений у вигляді: 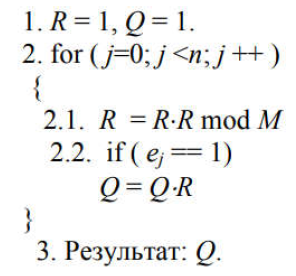 За такої реалізації алгоритму є потенційна можливість розпаралелити модульне експоненціювання. Аналіз зазначеного алгоритму показує, що базовими операціями виконання модулярного експонентування є зведення квадрат і модульне множення на фіксоване число, час виконання яких фактично визначається продуктивністю обчислення АЕ mod М. Більшість алгоритмів модулярного експоненціювання для реалізації згаданих двох операцій використовують єдину операцію множення. У свою чергу, час виконання модулярного множення визначається двома складовими: час, який необхідний для реалізації власне множення та час, що витрачається на модульну редукцію. У класичному множенні модульні редукції реалізуються з використанням операції розподілу і, відповідно, друга складова відіграє значну роль. Значна ефективність обчислювальної реалізації модулярного множення досягається при використанні алгоритму Монтгомері, в якому модульна редукція зводиться до зсуву на k розрядів. Тому на практиці при виконанні медулярного експоненціювання в більшості використовується алгоритм RSA-Монтгомері. Позначимо як Mont (A, B) множення Монтгомері, яке формує результат R = A * B * U mod M, де U модульна інверсія числа 2n по модулю M, тобто U = (2n) -1mod M. Алгоритм модулярного експонентування Монтгомері можна представити з використання введених нотацій таким чином: 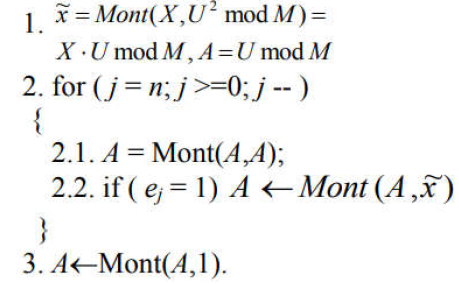 Лістинг програмного коду виконання завдання: using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows.Forms; using System.Collections; using System.Threading; namespace Prime_Numbers { public partial class Form1 : Form { bool working = false; int minN = 0; int maxN = 0; public Form1() { InitializeComponent(); } public static bool IsPrime(int n) { if (n > 1) { return Enumerable.Range(1, n).Where(x => n % x == 0).SequenceEqual(new[] { 1, n }); } return false; } private void run_Click(object sender, EventArgs e) { if (!working) { try { working = true; maxN = int.Parse(maxNumber.Text); minN = int.Parse(textBox1.Text); results.Text = ""; progress.Maximum = maxN; for (int i = minN; i <= maxN; i++) { Form1.ActiveForm.Update(); progress.Value = i; if (IsPrime(i)) { Console.WriteLine(i + " Просте число"); results.Text += i + "\r\n"; results.Update(); } else { Console.WriteLine(i + " Не просте число"); } } working = false; } catch (Exception ex) { progress.Value = 0; working = false; } } } private void label1_Click(object sender, EventArgs e) { } } } Результат запуску програми на виконання: 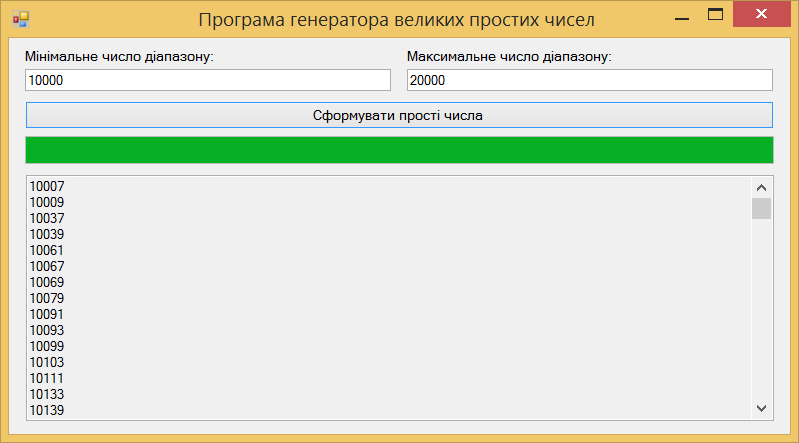 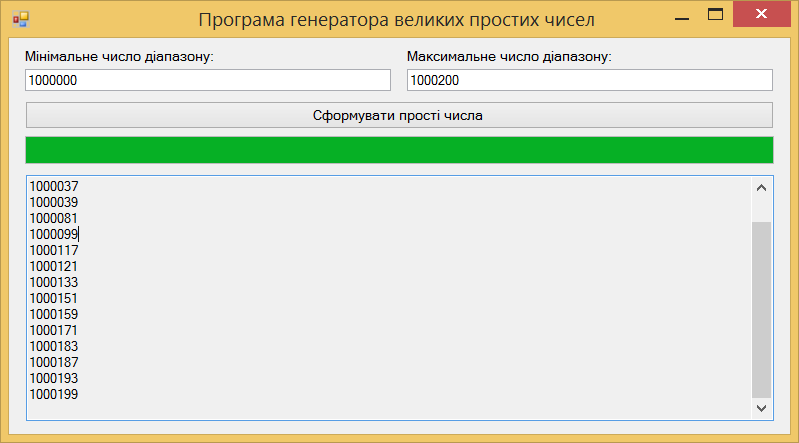 Лабораторна робота 5. Розробка програми керування ключами шифрування за схемою RSA. Дана реалізація криптосистеми складається з 4 основних класів: BigNumberGenerator – генератор великих чисел, як простих і звичайних. Для перевірки великої кількості на простоту було реалізовано імовірнісний тест Міллера-Рабіна. Тест Міллера – Рабіна – ймовірнісний поліноміальний тест простоти. Він дозволяє ефективно визначати, чи є задане число складеним. Однак з його допомогою не можна довести простоту простоти числа. Коротка суть його алгоритму така для визначення простоти числа m нам необхідно знайти r свідків простоти, і якщо вони знайдені, то число з високою ймовірністю є простим, якщо не знайдені, то число явно складене. Число r рекомендується брати як 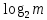 З теореми Рабіна випливає, що якщо r випадково вибраних чисел виявилися свідками простоти числа m, то ймовірність того, що m складне не перевищує 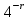 . Також вона стверджує, що складне непарне число m має не більше різних свідків простоти, де – функція Ейлера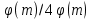 RSAGenerator – генератор ключів RSA, що працює за викладеним вище алгоритмом генерації ключів. Core - ядро програми, у ньому закладено й інші основні необхідні методи. Converter – клас працюючий з користувачем, тобто. той самий клас, який перетворює ваш текст на шифр-текст і навпаки. Час генерації ключів – випадкова величина, що з генерацією великого простого числа. Нижче наведено часовий інтервал генерації ключів на різних машинах. 10 тестів на ключ на машині Intel Pentium CPU B970 2.30 GHz з 6 Гб ОЗУ 64 bit – 0 секунд 128 bit – від 0 до 2 секунд 256 bit – від 0 секунд до 12 секунд 512 bit – від 0 секунд до 3 хвилин 13 секунд 1024 bit – від 58 секунд до 139 хвилин 35 секунд 2048 bit - за 3 години не завершився навіть перший тест 10 тестів на ключ на машині Intel Core i7 CPU 860 2.8GHz з 4 Гб ОЗУ 64 bit – 0 секунд 128 bit – від 0 до 2 секунд 256 bit – від 0 до 6 хвилин 13 секунд 512 bit – від 3 секунд до 3 хвилин 42 секунд 1024 bit – від 34 секунд до 112 хвилин 35 секунд 2048 bit - за 3 години не завершився навіть перший тест Лістинг програмного коду виконання завдання: using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Text; using System.Windows.Forms; using System.Security.Cryptography; using System.IO; using RSAEncryptionLib; namespace RSAEncryptionTester { public partial class MainForm : Form { RSAEncryption myRsa = new RSAEncryption(); public MainForm() { InitializeComponent(); } private void createKeyToolStripMenuItem_Click(object sender, EventArgs e) { RSACryptoServiceProvider rsa = new RSACryptoServiceProvider(); string privateKey = rsa.ToXmlString(true); File.WriteAllText(Application.StartupPath + "\\PrivateKey.xml", privateKey); string publicKey = rsa.ToXmlString(false); File.WriteAllText(Application.StartupPath + "\\PublicKey.xml", publicKey); MessageBox.Show("Ключ успешно создан по адресу:\n" + Application.StartupPath); } private void loadKeyToolStripMenuItem_Click(object sender, EventArgs e) { openKeyFileDialog.InitialDirectory = Application.StartupPath; якщо (openKeyFileDialog.ShowDialog() != DialogResult.OK) return; // Визначити, який пункт меню LoadKey було вибрано (загальнодоступний чи приватний) bool isLoadPrivate = (sender as ToolStripMenuItem).Name == "loadPrivateKeyToolStripMenuItem" ? true : false; try { if (isLoadPrivate) myRsa.LoadPrivateFromXml(openKeyFileDialog.FileName); // Завантажуємо приватний ключ до користувацького екземпляру RSA else myRsa.LoadPublicFromXml(openKeyFileDialog.FileName); // Або публічний ключ if (!chkShowData.Checked) // Чи хоче користувач бачити компоненти Key у формі? return; // Гадаю, що ні // Якщо хоче, то завантажуємо ключ в .NET RSA клас, щоб показати його компоненти у формі: RSACryptoServiceProvider localRsa = new RSACryptoServiceProvider(); localRsa.FromXmlString(File.ReadAllText(openKeyFileDialog.FileName)); RSAPпараметри rsaParams = localRsa.ExportParameters(isLoadPrivate); txtExponent.Text = GetHexString(rsaParams.Exponent); txtModulus.Text = GetHexString(rsaParams.Modulus); if (isLoadPrivate) txtD.Text = GetHexString(rsaParams.D); // Цей параметр є тільки в приватному ключі // Очищення екземпляру RSA localRsa.Clear(); } catch (Виключення ex) { MessageBox.Show("Помилка читання ключа,\nMessage: " + ex.Message); } } private void EncryptionToolStripMenuItem_Click(object sender, EventArgs e) { // Визначити, який пункт меню Шифрування було вибрано (загальнодоступний чи приватний) bool isEncryptPrivate = (sender as ToolStripMenuItem).Name == "privateEncryptionToolStripMenuItem" ? true : false; // Перевірити, чи в клас rsa завантажено правильний ключ if (isEncryptPrivate && !myRsa.IsPrivateKeyLoaded) { MessageBox.Show("Завантажте закритий ключ перед кодуванням."); return; } else if(!isEncryptPrivate && !myRsa.IsPublicKeyLoaded) { MessageBox.Show("Завантажте відкритий ключ перед кодуванням."); return; } try { byte[] message = Encoding.UTF8.GetBytes(txtMessage.Text); byte[] encMessage = null; if (isEncryptPrivate) // Виклик потрібного методу шифрування згідно з вибором користувача encMessage = myRsa.PrivateEncryption(message); else encMessage = myRsa.PublicEncryption(message); txtEncMsg.Text = Convert.ToBase64String(encMessage); } catch (Виключення ex) { MessageBox.Show("Помилка читання закодованих даних,\nMessage: " + ex.Message); } } private void DecryptionToolStripMenuItem_Click(object sender, EventArgs e) { // Визначити, який пункт меню Decryption було вибрано (загальнодоступний чи приватний) bool isDecryptPrivate = (sender as ToolStripMenuItem).Name == "privateDecryptionToolStripMenuItem" ? true : false; // Перевірити, чи в клас rsa завантажено правильний ключ if (isDecryptPrivate && !myRsa.IsPrivateKeyLoaded) { MessageBox.Show("Завантажте закритий ключ перед дешифруванням."); return; } else if(!isDecryptPrivate && !myRsa.IsPublicKeyLoaded) { MessageBox.Show("Завантажте відкритий ключ перед дешифруванням."); return; } try. { byte[] decMessage = Convert.FromBase64String(txtEncMsg.Text); byte[] message = null; if (isDecryptPrivate) // Виклик потрібного методу розшифрування згідно з вибором користувача message = myRsa.PrivateDecryption(decMessage); else message = myRsa.PublicDecryption(decMessage); рядок sMsg = Encoding.UTF8.GetString(message); MessageBox.Show("Повідомлення декодування:\n" + sMsg); } catch ((Exception ex) { MessageBox.Show("Помилка читання декодованих даних,\nMessage: " + ex.Message); } } private string GetHexString(byte[] byteArray) { Конструктор рядків hexString = new StringBuilder(byteArray.Length * 2); for (int i = 0; i < byteArray.Length; i++) hexString.Append(string.Format("{0:X}", byteArray[i])); int x = hexString.Capacity; return hexString.ToString(); } private void MainForm_FormClosing(object sender, FormClosingEventArgs e) { myRsa.Dispose(); } private void txtExponent_TextChanged(object sender, EventArgs e) { } } } Першим етапом є відкриття файлу rk.xtq з процесом та вказівки параметрів відображення. Ці налаштування виконуються після натискання кнопки OK. До кожного процесу передбачено виведення інформації про деталі шифрації-дешифрації. Робота з програмою починається після запуску файлу rsa.exe на виконання. На екрані з'являється головна форма управління програмою (рис.5.1) 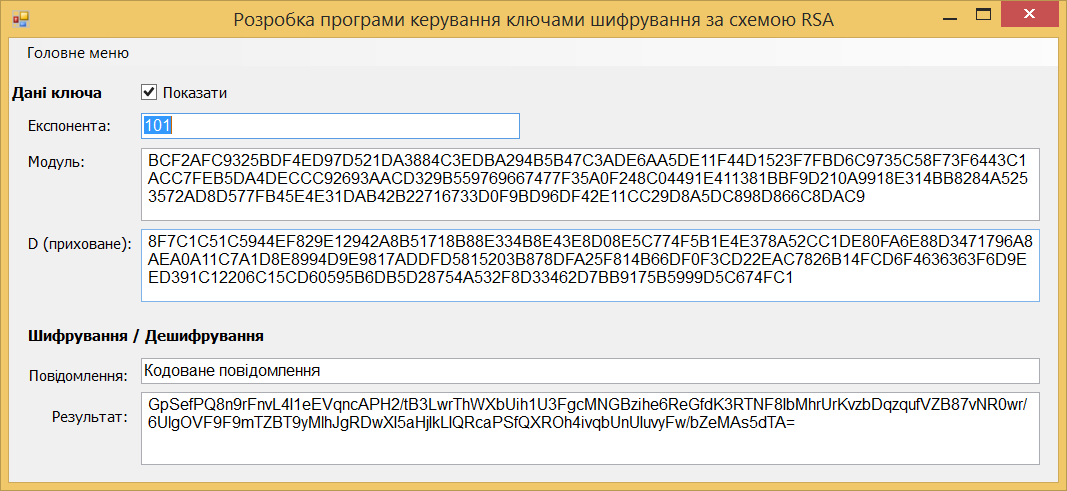 Рис. 5.1. Головне вікно програми, режим формування та завантаження ключів 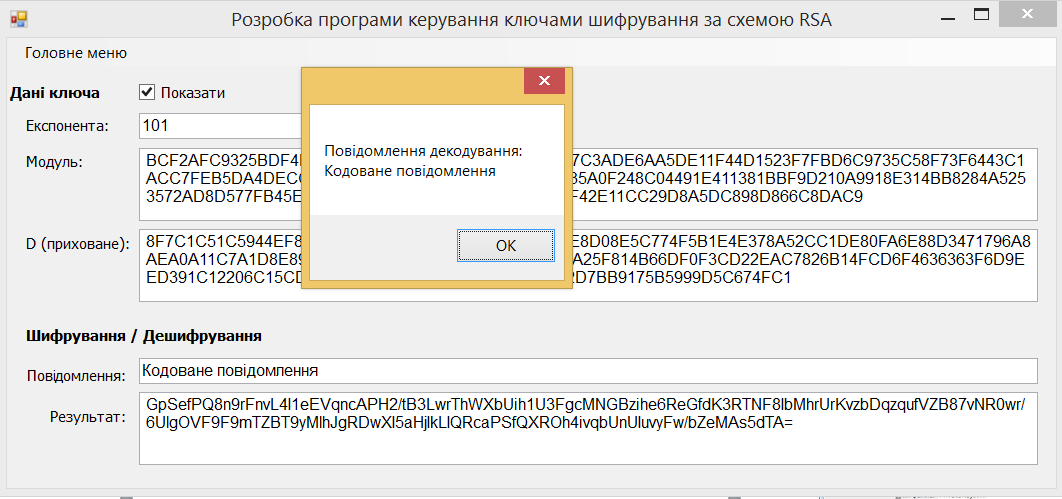 Рис. 5.2. Результат кодування Для переходу в режими роботи в головному меню представлені варіанти завантаження відкритих, закритих ключів, виконання шифрації-дешифрації з використанням відповідних ключів.  Рис. 5.3. Головне меню програми Для початку роботи виконується завантаження ключів після вибору пункту «Завантажити відкриті ключі», вказавши найменування файлу з даними ключа:  Рис. 5.4. Вибір відкритого ключа Для початку роботи виконується завантаження ключів після вибору пункту «Завантажити закриті ключі», вказавши найменування файлу з даними ключа PrivateKey.xml:  Рис. 5.5. Вибір закритого ключа Далі в текстове поле «Текст повідомлення» слід ввести текст, що кодується. Після цього з меню вибирається варіант шифрації – відкрита чи закрита. 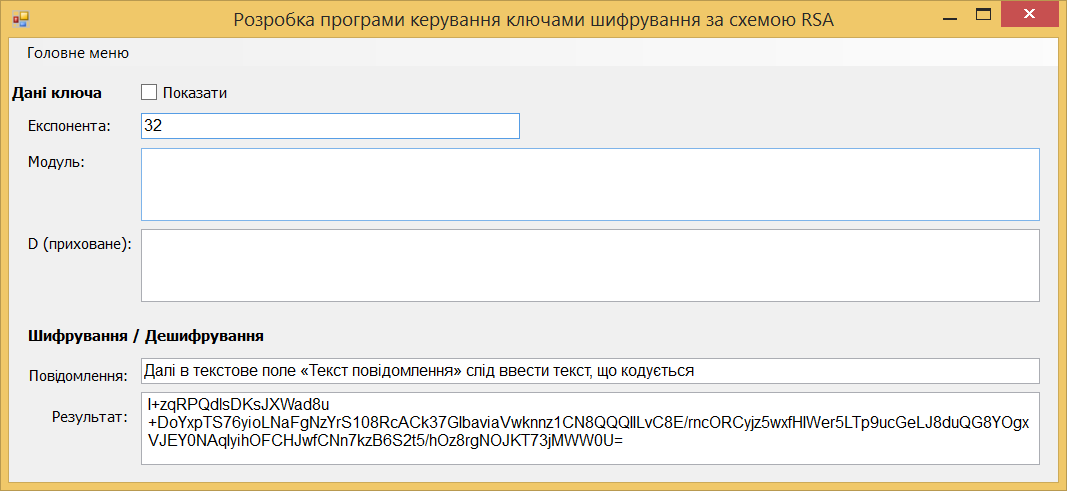 Рис. 5.6. Результат відкритого кодування При закритій системі результат шифрування коригується автоматично і з'являється у нижній частині вікна:  Рис. 5.7. Результат закритого кодування При помилці кодування при використанні неправильного ключа декодований текст має такий вигляд:  Рис. 5.8. Результат помилкового декодування - результат створення відкритих та закритих ключів: 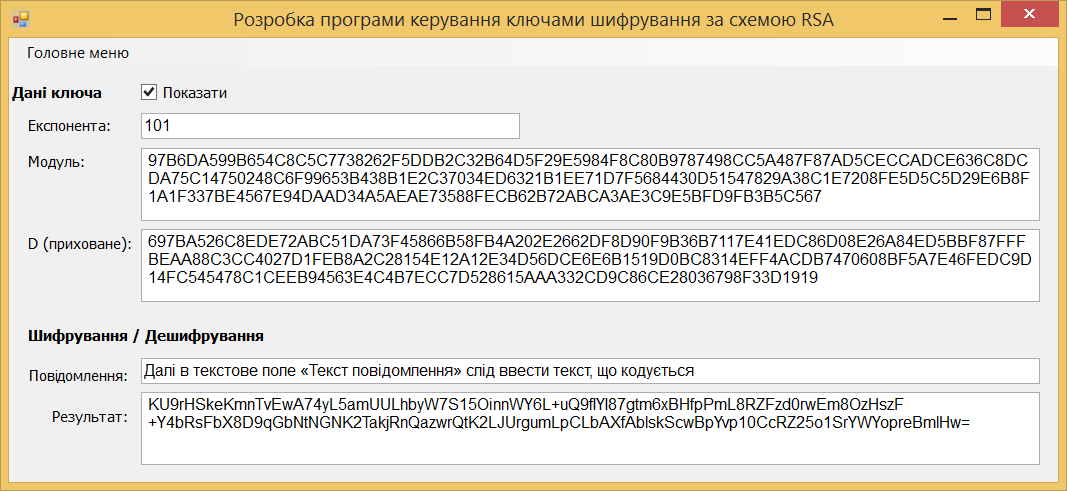 Рис. 5.9. Результат створення ключів та кодування Лабораторна робота 6. Розробка програми формування сигнатури повідомлення (цифровий підпис) на основі симетричного алгоритму шифрування. Програма реалізує два режими роботи: просте поблокове шифрування і дешифрування повідомлень (режим електронної кодової книги), а також зчеплення блоків шифру при формуванні цифрового підпису. Ефективними системами криптографічного захисту є асиметричні криптосистеми, звані також криптосистемами з відкритим ключем. У таких системах для шифрування даних використовується один ключ, а для дешифруванняінший ключ (звідси і назваасиметричні). Перший ключ є відкритим і може бути опублікований для всіх користувачів системи, які бажають зашифровувати дані. Неможливо дешифрувати дані за допомогою відкритого ключа. Для дешифрування даних використовує другий ключ, секретний. Зрозуміло, що ключ дешифрування не може бути визначений з відкритого ключа шифрування. Узагальнену схему асиметричної криптосистеми з відкритим ключем показано на рис. 6.1.
У цій криптосистемі застосовують два різні ключі: KB - відкритий ключ одержувача; kB - секретний ключ одержувача У. Значення ключів KB і kB залежить від початкового стану генератора ключів, вибираного випадковим чином. Розкриття секретного ключа kB за відомим відкритим ключем KB має бути обчислювально-нерозв'язною задачею, тобто. вимагати досить тривалого часу. Характерні особливості асиметричних криптосистем: Відкритий ключ KB і криптограма можуть бути відправлені незахищеними каналами, тобто. противнику відомі KB та С. Алгоритми шифрування (далі EK) та дешифрування (далі Dk) є відкритими. Захист інформації в асиметричній криптосистемі ґрунтується на секретності ключа kB. У. Діффі та М. Хеллман сформулювали вимоги, виконання яких забезпечує безпеку асиметричної криптосистеми: Обчислення пари ключів (KB, kB) одержувачем на основі початкової умови має бути простим. Відправник А, знаючи відкритий ключ KB і повідомлення М може легко обчислити криптограму С = EK (M). Одержувач В, використовуючи секретний ключ kB та криптограму Зможе легко відновити вихідне повідомлення M = Dk (С). Противник, знаючи відкритий ключ KB, намагаючись обчислити секретний ключ kB наштовхується на непереборну обчислювальну проблему. Оскільки прості числа повинні вибиратися таким чином, щоб факторизувати їхній добуток було обчислювально неможливо, рекомендується брати їх дуже великими і однаковою довжиною. Так, N довжини 1024 біта P і Q повинні бути довжиною приблизно 512 біт. Різниця чисел P та Q також не повинна бути маленькою, оскільки в цьому випадку PQ і, отже, P!Синтаксична помилка, N. Таким чином, розкладання N може бути знайдено простим розподілом на всі числа порядку!Синтаксична помилка, N. Числа P і Q повинні бути також стійкими простими числами. Число P є стійким (strong), якщо воно відповідає 3 умовам: P- 1 має великий простий дільник, позначимо його як r (тобто P = r + 1 (mod r)); P+ 1 має великий простий дільник, позначимо як s (тобто P = s 1 (mod s)); r- 1 має великий простий дільник, позначимо його як t (тобто r = 1 (mod t)). Умова 1 не дозволить успішно факторизувати N методом Полларда, який дозволяє швидко розкласти число N на множники, якщо P - 1 має невеликі (скажімо менше мільйона) прості дільники. Умова 2 дозволить захиститись від методу Ульямса, що дозволяє розкласти N за умови, що P + 1 має невеликі дільники. Умова 3 дозволить захиститись від методу безключового читання RSA (циклічної атаки). Якщо P вибирається випадково і має досить великий розмір, то, як правило, P – 1 та P+1 матимуть великі прості дільники. Проте вибір стійких простих чисел не захищає систему від атаки алгоритмом факторизації з урахуванням еліптичних кривих. Отримати стійкі прості числа можна в такий спосіб. Генеруємо великі прості числа s та t. Потім отримуємо таке число r, що r - 1 ділиться на t (для цього розглядаємо непарні числа виду kt + 1 де k - послідовні натуральні числа, і перевіряємо їх на простоту, поки не знайдемо просте). Потім обчислюючи P = ((sr - 1 - rs - 1) mod rs) + xrs, де x - деяке ціле число і перевіряючи P простоту, знаходимо стійке просте число P. Якщо число K вибирається випадковим чином, одним із способів прискорення обчислень (тобто зменшення числа зведень у ступінь) є наступний алгоритм швидкого зведення, наприклад: a25= ((a2a)2)2a. Таким чином, замість 25 множень виконується всього 6 (тобто 4 зведення квадрат і 2 множення на a). Формально алгоритм виглядає так: Вхід:aZn і ціле 0k Вихід:ak mod N. b= 1; if k = 0 then return b; A= a; if k0 = 1 then b = a; for i = 1 to t do 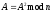 ;if ki=1 then b = Ab mod N; return b. На практиці зазвичай використовується K = 3, у цьому випадку необхідно, щоб ні P - 1, ні Q - 1 не ділилися на 3. При такому відкритому ключі операція шифрування виходить дуже швидкою і вимагає одне зведення квадрат і одне модульне множення (або 2 модульні множення - залежно від реалізації). Іншим часто використовуваним значенням є K = 216 + 1 = 65537Це число має дві одиниці в двійковому записі і вимагає, при використанні описаного алгоритму, 16 зведень квадрат і одне модульне множення. Така експонента має перевагу проти K = 3, оскільки у разі атака, описана раніше, не здійснитися, т.к. дуже мала ймовірність, що те саме повідомлення буде надіслано 216 + 1 абонентам. 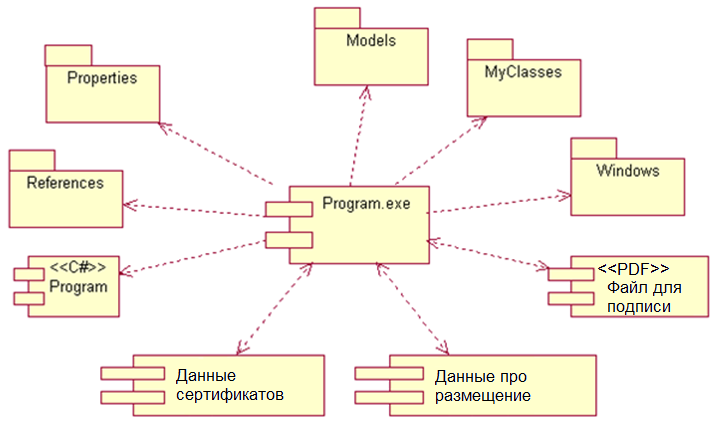 Рис. 6.2. Діаграма компонентів програми організації захищеного документу Розробка екранних форм введення-виведення та звітівЛістинг програмного коду виконання завдання: using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Text; using System.Windows.Forms; using iTextSharp.text.pdf; namespace iTextSharpSign { public partial class Form1 : Form { public Form1() { InitializeComponent(); } private void debug(string txt) { DebugBox.AppendText(txt + System.Environment.NewLine); } private void button4_Click(object sender, EventArgs e) { System.Windows.Forms.OpenFileDialog openFile; openFile = new System.Windows.Forms.OpenFileDialog(); openFile.Filter = "PDF files *.pdf|*.pdf"; openFile.Title = "Select a file"; if (openFile.ShowDialog() != DialogResult.OK) return; inputBox.Text = openFile.FileName; PdfReader reader = new PdfReader(inputBox.Text); MetaData md = new MetaData(); md.Info = reader.Info; authorBox.Text = md.Author; titleBox.Text = md.Title; subjectBox.Text = md.Subject; kwBox.Text = md.Keywords; creatorBox.Text = md.Creator; prodBox.Text = md.Producer; } private void button5_Click(object sender, EventArgs e) { System.Windows.Forms.SaveFileDialog saveFile; saveFile = new System.Windows.Forms.SaveFileDialog(); saveFile.Filter = "PDF files (*.pdf)|*.pdf"; saveFile.Title = "Save PDF File"; if (saveFile.ShowDialog() != DialogResult.OK) return; outputBox.Text = saveFile.FileName; } private void button2_Click(object sender, EventArgs e) { System.Windows.Forms.OpenFileDialog openFile; openFile = new System.Windows.Forms.OpenFileDialog(); openFile.Filter = "Certificate files *.pfx|*.pfx"; openFile.Title = "Select a file"; if (openFile.ShowDialog() != DialogResult.OK) return; certTextBox.Text = openFile.FileName; } private void button1_Click(object sender, EventArgs e) { debug("Started ..."); debug("Checking certificate ..."); Cert myCert=null; try { myCert = new Cert(certTextBox.Text, passwordBox.Text); debug("Certificate OK"); } catch (Exception ex) { debug("Error : please make sure you entered a valid certificate file and password"); debug("Exception : "+ex.ToString()); return; } debug("Creating new MetaData ... "); //Adding Meta Datas MetaData MyMD = new MetaData(); MyMD.Author = authorBox.Text; MyMD.Title = titleBox.Text; MyMD.Subject = subjectBox.Text; MyMD.Keywords = kwBox.Text; MyMD.Creator = creatorBox.Text; MyMD.Producer = prodBox.Text; debug("Signing document ... "); PDFSigner pdfs = new PDFSigner(inputBox.Text, outputBox.Text, myCert, MyMD); pdfs.Sign(Reasontext.Text, Contacttext.Text, Locationtext.Text, SigVisible.Checked, Convert.ToInt32(X.Text.ToString().Trim()), Convert.ToInt32(Y.Text.ToString().Trim()), Convert.ToInt32(X1.Text.ToString().Trim()), Convert.ToInt32(Y1.Text.ToString().Trim()), checkBox1.Checked, checkBox2.Checked, checkBox3.Checked,radioButton2.Checked); pdfs.Verify(); debug("Done :)"); } private void checkBox1_CheckedChanged(object sender, EventArgs e) { if (checkBox1.Checked == true) { Reasontext.Enabled = false; } if (checkBox1.Checked == false) { Reasontext.Enabled = true; } } private void checkBox2_CheckedChanged(object sender, EventArgs e) { if (checkBox2.Checked == true) { Contacttext.Enabled = false; } if (checkBox2.Checked == false) { Contacttext.Enabled = true; } } private void checkBox3_CheckedChanged(object sender, EventArgs e) { if (checkBox3.Checked == true) { Locationtext.Enabled = false; } if (checkBox3.Checked == false) { Locationtext.Enabled = true; } } private void radioButton2_CheckedChanged(object sender, EventArgs e) { if (radioButton2.Checked == true) { Reasontext.Enabled=false; Contacttext.Enabled=false; Locationtext.Enabled = false; checkBox1.Checked = true; checkBox2.Checked = true; checkBox3.Checked = true; } } private void radioButton1_CheckedChanged(object sender, EventArgs e) { Reasontext.Enabled = true; Contacttext.Enabled = true; Locationtext.Enabled = true; checkBox1.Checked = false; checkBox2.Checked = false; checkBox3.Checked = false; } } } Програмна реалізація криптосистеми підпису документа складається з 4 основних класів: Form1 – основна форма програми; PDFSigner - містить методи відкриття файлу, вбудовування елементів підпису у файл, збереження інформації; Cert – клас обробки даних сертифіката, що використовується для читання даних та вилучення парольної інформації; Resources –клас для організації вилучення стандартних ресурсів проекту; MetaData – клас для організації структури, яка є підсумковий набір даних для організації підпису документів; Setting – клас організації зміни налаштувань програми; Program – основний програмний клас програмного проекту. 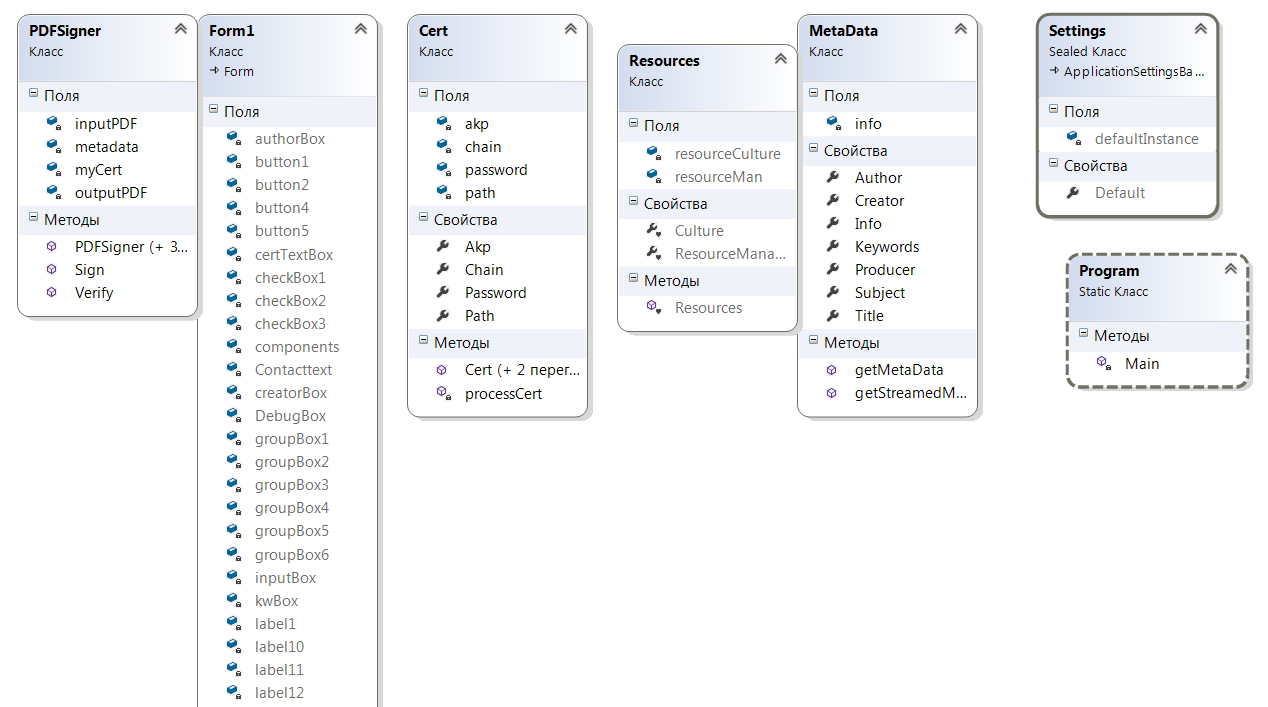 Рис. 6.3. Інтерфейс програми для впровадження цифрового підпису 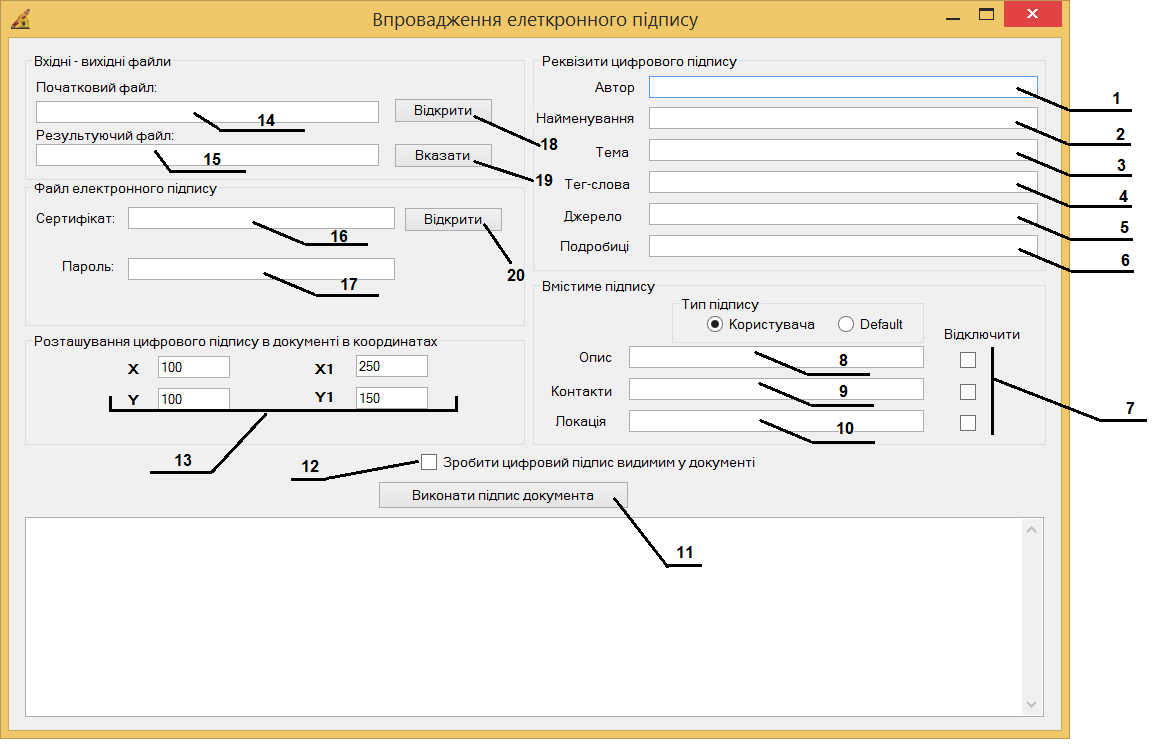 Рис. 6.4. Елементи головного вікна програми Компоненти головної форми програми:
Інтерфейс графічного додатка для впровадження цифрового підпису в документ має такий вигляд: 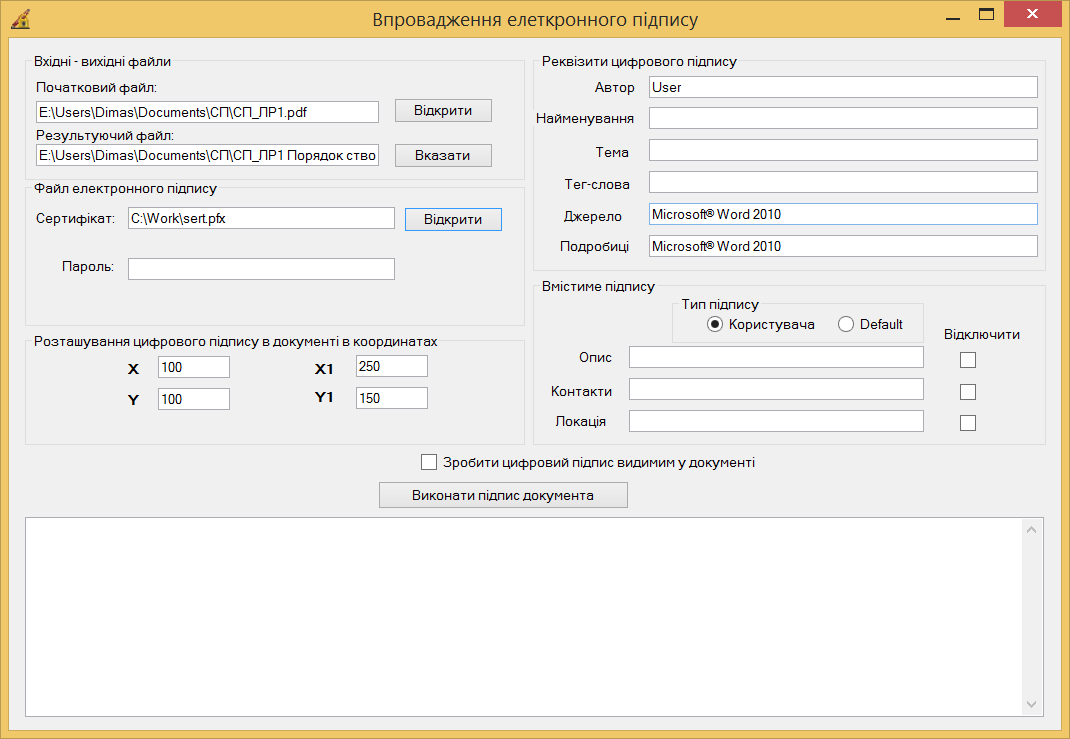 Рис. 6.5. Інтерфейс програми для впровадження цифрового підпису При запуску програми для генерування ключів кнопка Generate Key, потім вибирається Encrypt для кодування: 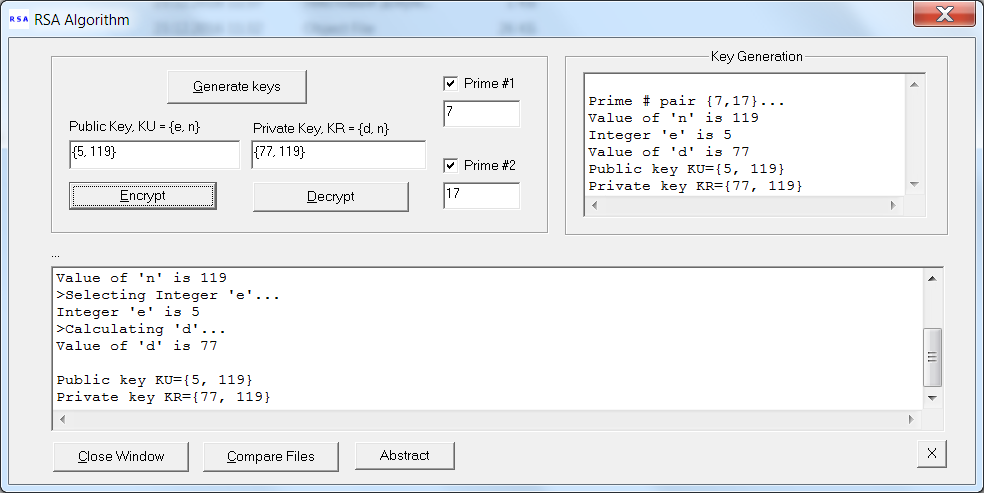 Рис. 6.6. Інтерфейс програми для формування ключів Вказуємо файл для кодування:  Рис. 6.7. Відкриття даних кодування Поточні процедури відображаються у консольному вікні:  Рис. 6.8. Виконання шифрації Результат кодування в окремому файлі з розширенням enc:  Рис. 6.9. Результат шифрації Для декодування натискаємо кнопку Decrypt, ключі головне не міняти на ті, якими кодували, та вказати закодований файл: |
