Отчет 1. Лабораторна робота 1 з аналізу даних Демянюк Лина 7 варіант Housing B
 Скачать 184.18 Kb. Скачать 184.18 Kb.
|
delve/data/boston/bostonDetail.html . Цільові дані (medv) – cередня вартість будинків, окупованих власниками, у 1000 доларів. Набір даних невеликий за розміром, лише 506 випадків. |
| 7. | Housing | B LSTAT |
У кожному випадку набору даних є 14 атрибутів. Вони є:
CRIM - рівень злочинності на душу населення по містах
ZN - частка житлових земель, зонованих для ділянок понад 25 000 кв. Футів.
INDUS - питома вага акцій нероздрібного бізнесу на місто.
CHAS - фіктивна змінна річка Чарльза (1, якщо тракт перетинає річку; 0 в іншому випадку)
NOX - концентрація оксидів азоту (частки на 10 мільйонів)
RM - середня кількість кімнат на помешкання
AGE - частка окупованих власником одиниць, побудованих до 1940 року
DIS - зважені відстані до п'яти бостонських центрів зайнятості
RAD - індекс доступності до радіальних автомобільних доріг
TAX - повна вартість ставки податку на нерухомість на 10000 доларів
PTRATIO - співвідношення учня-вчителя за містом
B - 1000 (Bk - 0,63) ^ 2, де Bk - частка негрів в місті
LSTAT -% нижчий статус населення
MEDV - Середня вартість будинків, окупованих власниками, у 1000 доларів
Розбити дані на навчальну та тестову вибірки та перевірити їх репрезентативність.
Експериментальні дані розіб’ємо на навчальну та тестову вибірки. В навчальну включимо непарні рядки даних, а в тестову – парні. Для перевірки репрезентативності вибірок розрахуємо математичне сподівання (mean) та дисперсію (std) даних за кожною змінною.
| Вибірка | mean(x1) | mean(x2) | mean(y) | std(x1) | std(x2) | std(y) |
| Навчальна | 11,57 | 6,27 | 68,65 | 23,50 | 0,72 | 27,91 |
| Тестова | 11,16 | 6,30 | 68,50 | 23,18 | 0,68 | 28,44 |
Результати перевірки вказують на приблизно однакові значення цих показників для навчальної та тестової вибірок, тому вважаємо їх репрезентативними. Візуально підтверджує цей висновок рисунок:
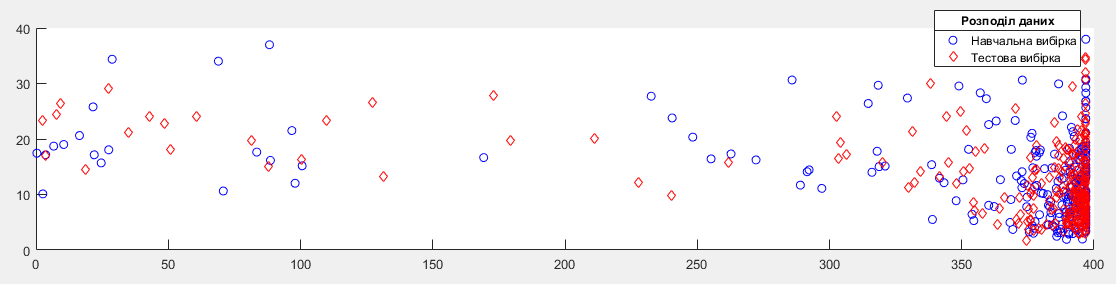
Рисунок 1. Розподіл даних навчальної та тестової вибірок
За допомогою такого коду:
filename = 'D:\housing.data';
formatSpec ='%8f%7f%8f%3f%8f%8f%7f%8f%4f%7f%7f%7f%7f%f%[^\n\r]';
fileID = fopen(filename,'r');
dataArray = textscan(fileID, formatSpec, 'Delimiter', '', 'WhiteSpace', '', 'ReturnOnError', false);
fclose(fileID);
housing = [dataArray{1:end-1}];
clearvars filename formatSpec fileID dataArray ans;
data = housing;
vars = [12, 13, 14];
x1 = data(:,vars(1));
x2 = data(:,vars(2));
y = data(:,vars(3));
%Формування навчальної та тестової вибірок:
tr_set = data(1:2:end, vars);
test_set = data(2:2:end, vars);
%математичне сподівання
mn_tr = mean(tr_set);
mn_test = mean(test_set);
%дисперсія
despers_tr = std(tr_set);
despers_test = std(test_set);
%графік розподіл вибірки
subplot(2,1,1)
scatter(tr_set(:,1),tr_set(:,2),'b','o');
hold on
scatter(test_set(:,1),test_set(:,2),'r','d');
l = legend('Навчальна вибірка','Тестова вибірка');
title(l,'Розподіл даних');
Зобразити експериментальні дані у формі однофакторних залежностей.
Однофакторні залежності вказують на слабку тенденцію збільшення середньої вартості будинків зі збільшенням частки негрів у місті.
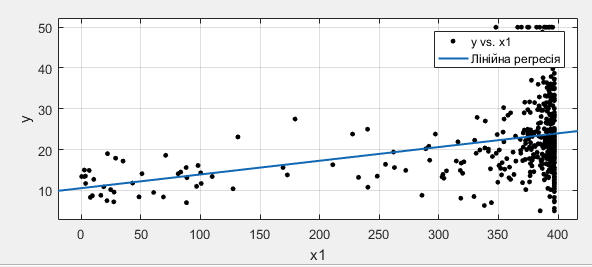
Рисунок 2. Залежність між х1 та у.
Однофакторні залежності вказують на на сильну тенденцію зменшення середньої вартості будинків зі збільшенням % статусу населення.
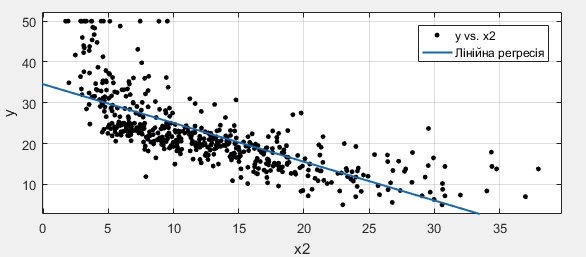
Рисунок 3. Залежність між х2 та у.
За допомогою такого коду:
%Однофакторні залежності
cftool(x1,y);
cftool(x2,y);
Знайдемо коефіцієнти лінійної регресії за допомогою такої програми:
??????
%Довжина вибірки:
M_tr=length(tr_set);
M_test=length(test_set);
disp('Лінійний регресійний аналіз:')
%model_1 y = a0 + a1x1 + a2x2
X_tr=[ones(M_tr,1) tr_set(:,1) tr_set(:,2)];
X_test=[ones(M_test,1) test_set(:,1) test_set(:,2)];
%model_2 y = a0 + a1x1 + a2x2 + a3x1^2 + a4x2^2
X_tr=[ones(M_tr,1) tr_set(:,1) tr_set(:,2) tr_set(:,1).*tr_set(:,1) tr_set(:,2).*tr_set(:,2)];
X_test=[ones(M_test,1) test_set(:,1) test_set(:,2) test_set(:,1).*test_set(:,1) test_set(:,2).*test_set(:,2)];
%model_3 y = a0 + a1x1 + a2x2 + a3x1^2 + a4x2^2 + a5x1x2
X_tr=[ones(M_tr,1) tr_set(:,1) tr_set(:,2) tr_set(:,1).*tr_set(:,1) tr_set(:,2).*tr_set(:,2) tr_set(:,1).*tr_set(:,2)];
X_test=[ones(M_test,1) test_set(:,1) test_set(:,2) test_set(:,1).*test_set(:,1) test_set(:,2).*test_set(:,2) test_set(:,1).*test_set(:,2)];
%model_4 y = a0 + a1x1 + a2x2 + a3x1x2
X_tr=[ones(M_tr,1) tr_set(:,1) tr_set(:,2) tr_set(:,1).*tr_set(:,2)];
X_test=[ones(M_test,1) test_set(:,1) test_set(:,2) test_set(:,1).*test_set(:,2)];
%model_5 y = a0 + a1x1 + a2x2 + a3sqrt(x1) + a4sqrt(x2)
X_tr=[ones(M_tr,1) tr_set(:,1) tr_set(:,2) sqrt(tr_set(:,1)) sqrt(tr_set(:,2))];
X_test=[ones(M_test,1) test_set(:,1) test_set(:,2) sqrt(test_set(:,1)) sqrt(test_set(:,2)];
Аналогічно знайдемо інші регресійні моделі та запишемо результати у таблицю.
| № | Модель | RMSEtr | RMSEtest |
| 1 | y = 29.65042+0.01136 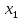 –0.87163 –0.87163 | 6.203 | 6.168 |
| 2 | y = 38.12437+0.02656 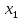 –2.29542 –2.29542 –0.00004 –0.00004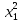 +0.04308 +0.04308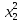 | 5.372 | 5.567 |
| 3 | y = 37.94621+0.02704 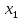 –2.28416 –2.28416 –0.00004 –0.00004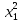 +0.04298 +0.04298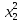 –0.00002 –0.00002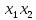 | 5.372 | 5.567 |
| 4 | y = 14.46222+0.05286 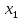 –0.08665 –0.08665 –0.00222 –0.00222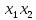 | 6.025 | 6.166 |
| 5 | y =63.34713+0.00391 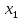 +1.81738 +1.81738 +0.1623 +0.1623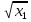 –19.95681 –19.95681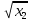 | 5.14 | 5.368 |
З таблиці, що наведено вище, бачимо що досліджувані моделі мають від 3 до 6 коефіцієнтів. Найкраща точність спостерігається для 5 моделі, що має 5 коефіцієнтів, а найгірша для 1 моделі, яка має 3 коефіцієнта. Порівнюючи теоретичні результати з експериментальними даними бачимо, що для моделі 1 характерне завишення прогнозованої ціни будинків, а для моделі 5 нев’язка майже рівномірно розподілена та теоритичні дані узгоджуються з експерементальними.
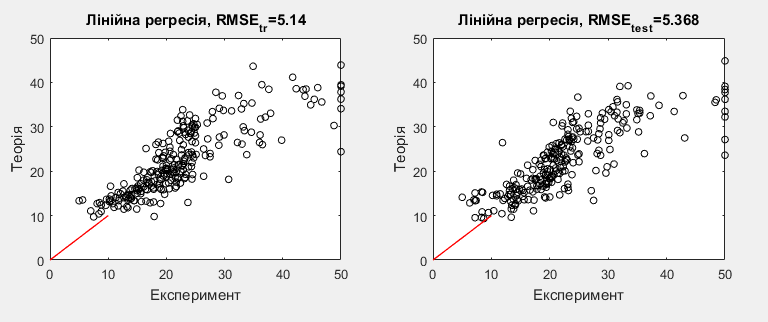
Рис.4 Модель 5.
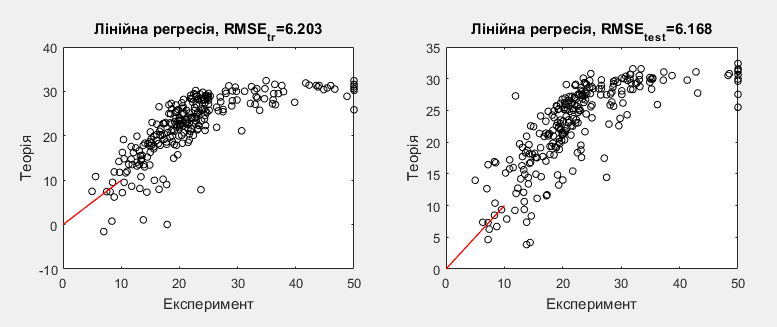
Рис.5 Модель 1.
Додаємо у постановку задачі ще одну вхідну зміну RM (середня кількість кімнат в будинку). Очевидно, що чим більше кімнат тим дорожча вартість.
x3 = data(:,6);
вносимо зміну в модель та знаходимо цю модель під коренем.
| № | Модель | RMSEtr | RMSEtest |
| 5 | y =63.34713+0.00391 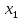 +1.81738 +1.81738 +0.1623 +0.1623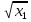 –19.95681 –19.95681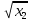 | 5.14 | 5.368 |
| 6 | y =12,7415–0,00144 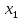 +1,69379 +1,69379 +0,34205 +0,34205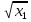 –17,36588 –17,36588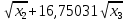 | 4.851 | 4.925 |
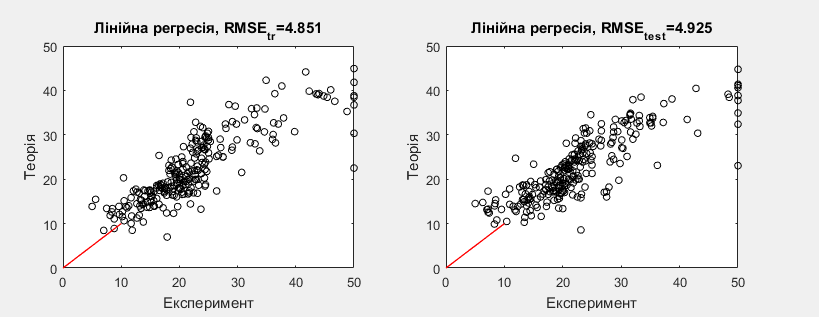
Рис.7 Модель 6.
Отримана модель значно точніша, при цьому ртохи складніша від 5, має 6 коефіцієнтів. Нев’язка більш розподілена рівномірно та не сильно відхиляється від лінії регресії.
Порівняння з іншими моделями.
Наша модель поступається по точності тільки кубічній, але по складності отримана модель більш проста.
| Модель | Кількість входів | Кількість коефіцієнтів | RMSEtr | RMSEtest | Інтерпретабельність |
| Власна модель | 3 | 6 | 4.851 | 4.925 | висока |
| Лінійна | 2 | 3 | 5.637 | 5.137 | висока |
| Кубічна | 3 | 10 | 3.96 | 3.94 | висока |
