Лаба 1 скорость звука постоянная адиабаты. Лабораторная 1 Скорость звука и адиабатическая постоянная газов Цель работы определения скорости распространения звуковой волны в воздухе и расчет показателя адиабаты для него. Краткая теория
 Скачать 1.71 Mb.
|
|
Лабораторная 1 Скорость звука и адиабатическая постоянная газов Цель работы: – определения скорости распространения звуковой волны в воздухе и расчет показателя адиабаты для него. Краткая теория Механические колебания, возникшие в какой-либо точке упругой среды, передаются другим точкам, вызывая смещение их из положения равновесия. Процесс распространения колебаний в среде называется механической волной. При этом колеблющиеся частицы не перемещаются с распространяющимся волновым процессом, а колеблются около равновесных положений. В продольной волне колебания частиц происходят в направлении распространения волны, а в поперечной они перпендикулярны направлению распространения колебаний. Будут ли волны продольными или поперечными в данной среде определяют упругие свойства ее. В жидкостях и газах распространяются только продольные механические волны, так как в них не возникают упругие силы, стремящиеся возвратить сдвинутый слой в положение равновесия. В твердых телах могут распространяться и продольные, и поперечные механические волны. Уравнение бегущей вдоль оси X волны записывается в виде: 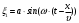 где ξ1 – текущее значение отклонения, a – амплитуда (максимальные значения ξ), ω – циклическая частота колебаний; t – время; x – координата; υ – скорость распространения волны. Под скоростью распространения волны понимают фазовую скорость, то есть скорость распространения данной фазы колебания, например, максимума смещения точки. Расстояние, на которое распространяется данная фаза колебаний за период, называется длиной волны λ. Ее можно определить также как наименьшее расстояние между точками, колеблющимися в одинаковых фазах. Для волн высокой частоты, какими являются звуковые волны, процессы сжатия – разрежения можно считать происходящими без теплообмена, то есть адиабатическими, которые описываются уравнением Пуассона p·V γ const, где γ – показатель адиабаты. Известно что E p. Из уравнения Клапейрона Менделеева следует R·T/(M·p) где М – молекулярный вес, R – универсальная газовая постоянная, T – температура в Кельвинах. Откуда следует M·2/(R·T) Таким образом, определение показателя адиабаты сводится к измерению скорости звука и абсолютной температуры. Скорость звука определяется при исследовании интерференции (сложения) звуковых волн при отражении от преграды, приводящей к образованию стоячей волны. Описание установки Для проведения опытов используется электронный блок ИСТ-4 и РЕЗОНАТОР (модуль 04). РЕЗОНАТОР содержит металлическую трубку 1 и ПУЛЬТ 6, рис. 1.1. Один торец трубки закрыт крышкой, а другой – динамиком 4 и микрофоном 5. В трубку внедрен датчик температуры 3. Динамик подключен к генератору гармонического сигнала, микрофон – к индикатору резонанса (оба устройства входят в состав ПУЛЬТА). Сопротивление нагревательной обмотки 12…14 Ом, максимальное напряжение на обмотке – 20 В. ПУЛЬТ резонатора содержит генератор с регулируемой амплитудой и частотой (700–3000 Гц), цифровой частотомер с 4-разрядным индикатором Н1, индикатор резонанса (светодиод) Н2, ручки регулировки частоты и амплитуды, разъема 7. Электропитание всех устройств производится через разъем 7, подключаемый через кабель к разъему ОБЪЕКТ на ИСТ-4. Назначение контактов разъема приведено в описании ИСТ-4, при этом контакт датчика Д2 не задействован. Питание генератора осуществляется через шины +12 и ОБЩ.СИЛ. 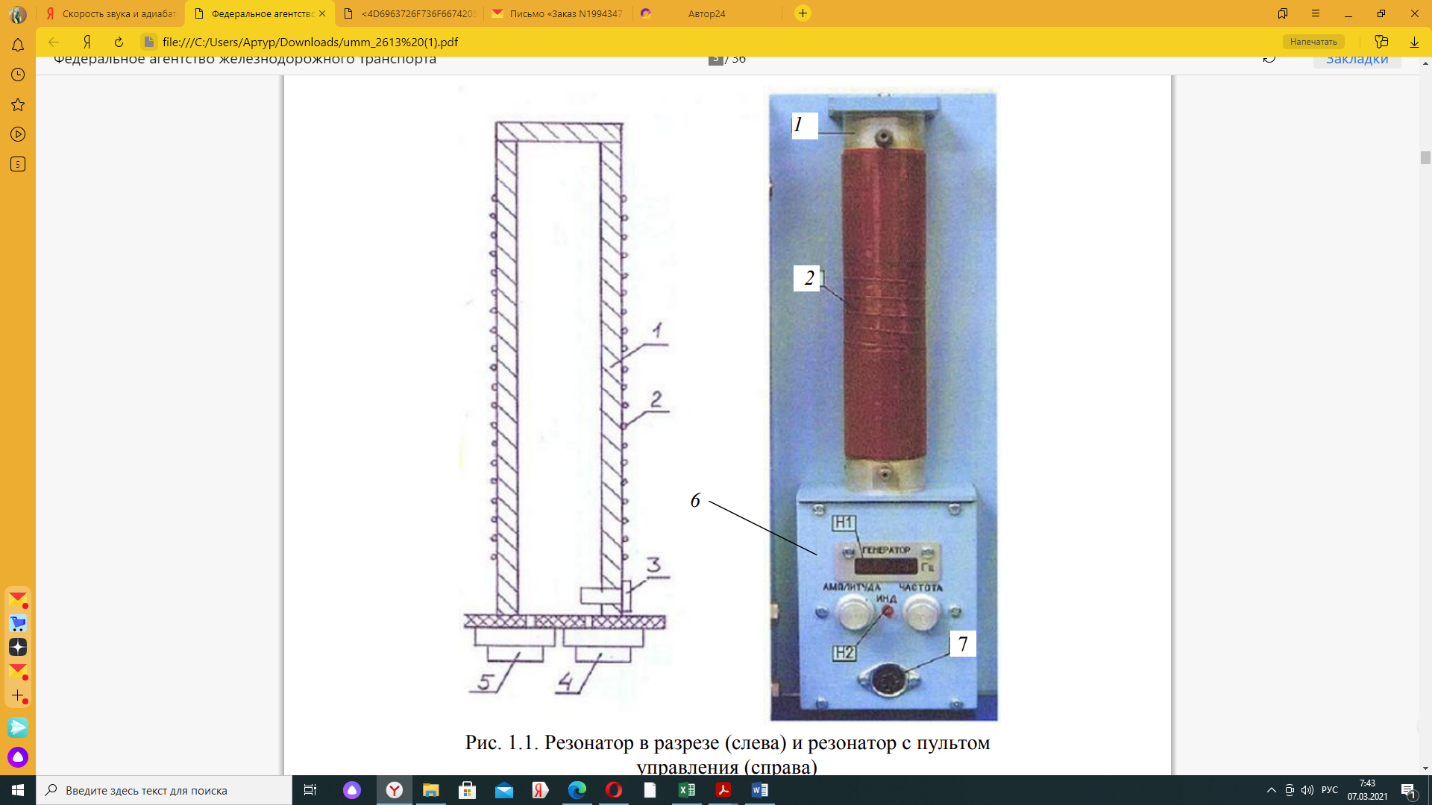 Рис. 1.1. Резонатор в разрезе (слева) и резонатор с пультом управления (справа) 1 – металлически цилиндр; 2 – обогреватель; 3 – датчик температуры; 4 – динамик; 5 – микрофон; 6 – пульт управления; 7 – разъем для подсоединения электронного блокаИзменяя частоту сигнала, по максимуму амплитуды находят резонансные частоты. Скорость звука определяется по формуле: fN=N·υ/(2·L). где N = 1, 2, 3,…– номер резонансной частоты, v – скорость звука, L = 180 мм – длина трубы. 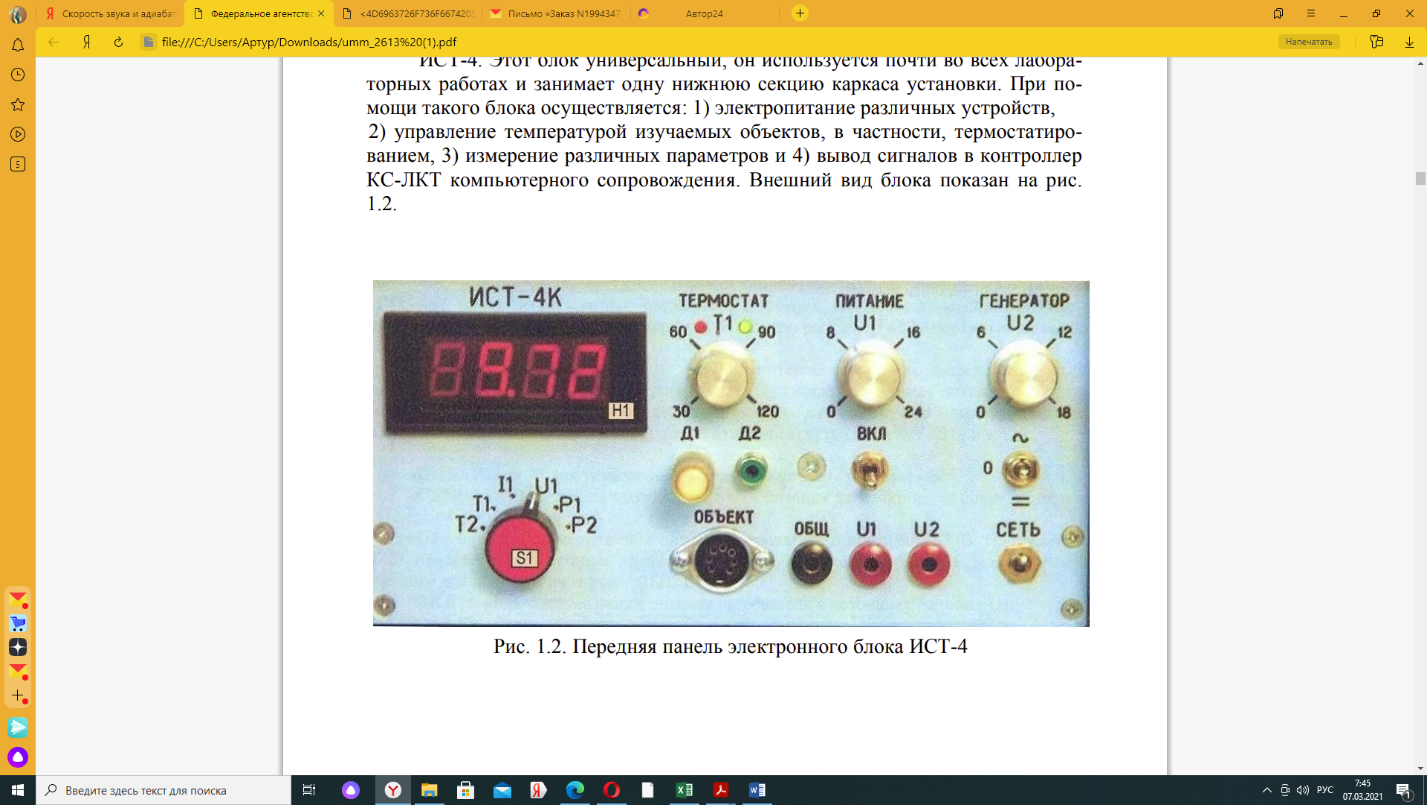 Рис. 1.2. Передняя панель электронного блока ИСТ-4ИСТ-4. Этот блок универсальный, он используется почти во всех лабораторных работах и занимает одну нижнюю секцию каркаса установки. При помощи такого блока осуществляется: 1) электропитание различных устройств, 2) управление температурой изучаемых объектов, в частности, термостатированием, 3) измерение различных параметров и 4) вывод сигналов в контроллер КС-ЛКТ компьютерного сопровождения. Внешний вид блока показан на рис. 1.2. Выполнение работы Установим блок СВОЙСТВА ГАЗОВ к разъему ОБЪЕКТ ИСТ-4. Включим ИСТ-4 и убедившись в работе генератора по звуку динамика и нагревателя по наличию тока нагрузки при подаче напряжения на нагреватель. По максимуму амплитуды, регистрируемой индикатором Н2 (рис. 1.1), определим резонансные частоты для двух гармоник при двух-трех температурах от комнатной до 110оС. После стабилизации термостатом каждого значения температуры измерим напряжение и ток в обмотке нагревателя. Установим рабочее напряжение примерно равным 18…20 В и задайте нужное значение температуры регулятором Т1 блока ИСТ-4. Значение скорости звука v и значение γ = cp /cv определяют как среднее по двум или трем резонансным частотам, длину резонатора принимают равной L = 180 мм. υN= 2·L·fN /N, γ= υср2·М/(R·T) , где М = 29 кг/кмоль – молекулярная масса, R = 8,314 кДж/(кмоль К) – газовая постоянная, T – температура по шкале Кельвина. Получим следующие результаты измерений
Средняя по диапазону температур от 15ºС до 90ºС постоянная Пуассона равна γср=1,46. Выводы Постоянная адиабаты ля воздуха близка к 1,4, что соответствует тому. что основную часть воздуха составляют двухатомные кислород и азот. Также заметно снижение постоянной адиабаты с ростом температуры. |