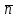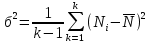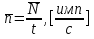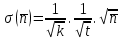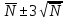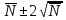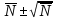|
|
Лабораторная работа . 1 Гамма излучение радиоактивных нуклидов выполнил студент Нго Тан Фу Чан Тхиен Фонг
Санкт-Петербургский политехнический университет Петра великого
Институт энергетики и транспортных систем
Кафедра «Экспериментальная Ядерная Физика»
Лабораторная работа №.1
ГАММА – ИЗЛУЧЕНИЕ РАДИОАКТИВНЫХ НУКЛИДОВ
Выполнил студент
|
Нго Тан Фу
Чан Тхиен Фонг
|
Группа
|
23221/6
|
Преподаватель
|
Бакаев В.А
|
Санкт – Петербург
2017
Введение
Гамма-излучение по своей физической природе является коротковолновым электромагнитным излучением, которое возникает при изменении энергетического состояния атомных ядер, при ядерных превращениях или при аннигиляции частиц.
Гамма-излучения радиоактивных нуклидов в основном связано с возбуждеными ядрами. При испускании гамма-квантов эти ядра переходят из возбужденного состояния в основное.
Гамма-излучение относится к косвенному ионизирующему излучению, т.е к излучению, состоящему из незаряженных частиц, создающему в веществе в результате своих взаимодействий заряженные частицы, которые ионизируют это вещество.
В данной работе для измерения мощности гамма-излучателей применен стационарный гамма-радиометр, состоящий из источника высокого напряжения БВ-2-2, детектора – сцинтилляционного счетчика, помещенного для уменьшения фона в свициовый домик типа ДС, и пересчетного прибора ПС02-4.
В работе используотся источники гамма-излучения 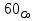 с периодом полураспада 5,27 года. При одном акте распада с периодом полураспада 5,27 года. При одном акте распада 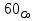 испускается два гамма-кванта с энергиями 1,17 и 1,33 МэВ. испускается два гамма-кванта с энергиями 1,17 и 1,33 МэВ.
ПРОВЕРКА ИСПРАВНОСТИ ГАММА – РАДИОМЕТРА
Источник №.13
Напряжение 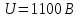
Таблица 1
Результаты измерений и расчетов
Номер измер-ения i
|
Длительн-ость измерения в серии t, с
|
Измеренное число импульсов 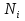 , имп , имп
|
Среднее число импульсов в серии 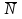 ,имп ,имп
|
Максималь-ное отклонение от 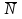 в серии в серии 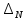 , имп , имп
|
Оценка дисперсии числа импульсов в серии 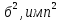
|
1
|
1
|
27
|
24
|
22
|
26
|
28
|
25.4
|
3.4
|
5.8
|
2
|
3
|
86
|
80
|
82
|
79
|
86
|
82.6
|
3.6
|
10.8
|
3
|
10
|
287
|
303
|
301
|
299
|
299
|
297.8
|
10.8
|
39.2
|
4
|
30
|
874
|
880
|
904
|
874
|
896
|
885.6
|
18.4
|
186.8
|
5
|
100
|
3016
|
2916
|
2955
|
3031
|
2933
|
2970.2
|
60.8
|
2586.7
|
Таблица 2
Номер измер-ения i
|
Длительность измерения в серии t, с
|
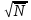
|
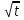
|
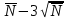
|
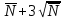
|
Средняя скорость счета радиометра 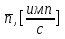
|
Предел ошибок 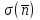
|
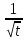
|
Максималь-ное отклонение “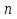 ” от ” от 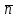
|
1
|
1
|
5.04
|
1.00
|
10,28
|
40,52
|
25,40
|
2,25
|
1.000
|
3.40
|
2
|
3
|
9.09
|
1.73
|
55,33
|
109,87
|
27,53
|
1,35
|
0.577
|
1.20
|
3
|
10
|
17.26
|
3.16
|
246.03
|
349.57
|
29.78
|
0,77
|
0.316
|
1.08
|
4
|
30
|
29.76
|
5.48
|
796,32
|
974,88
|
29,52
|
0,44
|
0.183
|
0.61
|
5
|
100
|
54.50
|
10.00
|
2806,70
|
3133,70
|
29,70
|
0,24
|
0.100
|
0.61
|
Формулы для расчетов:
Дисперсия : 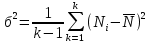
Средняя скорость счета 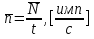
Предел ошибок 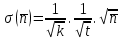
Вывод по результатам измерений:
Среднее число импульсов прямо пропорционально времени измерения
Максимальное отклонение i – ого измерения от среднего в серии увеличивается при увеличении 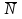 пропорционально пропорционально 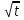 или или 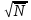
Оценка дисперсии б увеличивается прямо пропорционально 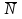 или t или t
При любом времени экспозиции разброс числа импульсов заключен в интервале 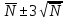
Таким образом, что измеренное число импульсов N подчиняется закону Пуассона
Величина средней скорости 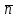 не зависит, в пределах ошибок, от времени измеренния не зависит, в пределах ошибок, от времени измеренния
Максимальное отклонение i – ого измерения скорости счета от среднего в серии уменьшается при увеличении времени измерения как 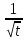 . => для увеличения точноcти измерений необходимо увеличивать время измерения . => для увеличения точноcти измерений необходимо увеличивать время измерения
Общий вывод (о исправности гамма-радиометра):
По результатам измерений – это исправный гамма–радиометр
ИССЛЕДОВАНИЕ ФЛУКТУАЦИЙ ОТСЧЕТОВ ПРИ РЕГИСТРАЦИИ ИОНИЗИРУЮЩЕГО ИЗЛУЧЕНИЯ
Таблица 3
Результаты измерений и расчетов
Длительность измерения в серии t, с
|
|
1
|
3
|
10
|
Измеренное число импульсов 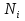 , имп , имп
|
29
|
28
|
26
|
39
|
26
|
108
|
74
|
98
|
97
|
90
|
299
|
301
|
303
|
284
|
287
|
42
|
41
|
27
|
34
|
31
|
83
|
80
|
93
|
76
|
94
|
299
|
348
|
270
|
307
|
295
|
17
|
21
|
30
|
33
|
22
|
88
|
69
|
87
|
94
|
108
|
322
|
267
|
284
|
273
|
321
|
33
|
26
|
29
|
30
|
32
|
81
|
80
|
102
|
83
|
96
|
297
|
286
|
306
|
281
|
315
|
25
|
36
|
26
|
28
|
32
|
85
|
92
|
94
|
99
|
102
|
322
|
279
|
324
|
299
|
313
|
36
|
24
|
26
|
29
|
23
|
103
|
72
|
85
|
82
|
104
|
287
|
306
|
291
|
306
|
280
|
27
|
34
|
29
|
26
|
41
|
94
|
90
|
109
|
92
|
84
|
290
|
288
|
290
|
289
|
304
|
Продолжение таблицы 3
|
24
|
29
|
33
|
25
|
27
|
80
|
78
|
90
|
98
|
99
|
318
|
298
|
291
|
309
|
294
|
29
|
21
|
28
|
37
|
33
|
96
|
97
|
106
|
101
|
94
|
312
|
293
|
283
|
301
|
283
|
29
|
39
|
34
|
28
|
34
|
87
|
85
|
92
|
77
|
95
|
282
|
302
|
294
|
278
|
309
|
Таблица 4
Номер измер-ения i
|
Длительн-ость измерения в серии t, с
|
Среднее число импульсов в серии 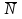 ,имп ,имп
|
Максималь-ное отклонение от 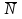 в серии в серии 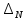 , имп , имп
|
Оценка дисперсии числа импульсов в серии 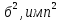
|
Число измерений выходит за интервал  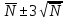
|
Число измерений попадает в интервал 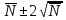
|
Число измерений попадает в интервал  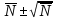
|
1
|
1
|
29.76
|
12.76
|
30.35
|
0
|
47
|
37
|
2
|
3
|
90.86
|
21.86
|
97.84
|
0
|
50
|
32
|
3
|
10
|
297.20
|
50.8
|
250.00
|
0
|
49
|
38
|
Вывод:
Максимальное отклонение от среднего в серии из 50 измерений маметно превышает максимальное отклонение в серии из 5 измерений при той же экспозиции.
Вероятность измерения 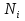 , близких к , близких к 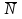 , больше, чем далеко отстоящих , больше, чем далеко отстоящих 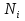
Величины оценки дисперсии для серий из 5 и 50 измерений отличаются друг от друга
Длительность измерения в серии t, с
|
Оценка дисперсии числа импульсов в серии 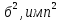
|
5 измерений
|
50 измерений
|
1
|
5.8
|
30.35
|
3
|
10.8
|
97.84
|
10
|
39.2
|
250.00
|
Оценка дисперсии “б” увеличивается прямо пропорционально 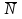
|
|
|
 Скачать 27.99 Kb.
Скачать 27.99 Kb.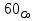 с периодом полураспада 5,27 года. При одном акте распада
с периодом полураспада 5,27 года. При одном акте распада 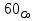 испускается два гамма-кванта с энергиями 1,17 и 1,33 МэВ.
испускается два гамма-кванта с энергиями 1,17 и 1,33 МэВ.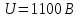

 , имп
, имп ,имп
,имп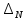 , имп
, имп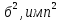
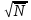
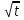
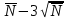
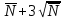
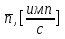
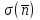
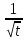
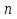 ” от
” от