Лабораторная работа Применение нейронных сетей для задач классификации и кластеризации Задание
 Скачать 342.88 Kb. Скачать 342.88 Kb.
|
Лабораторная работа № 1. Применение нейронных сетей для задач классификации и кластеризацииЗадание. Сгенерировать случайные числа по указанному закону распределения. Из них создается матрица из M строк (наблюдений) и K столбцов (признаков). Сгенерированные строки должны принадлежать одному из N классов за счет прибавления к сгенерированным числам положительной или отрицательной добавки (функция) Все признаки должны быть числовыми и нормализованными (находиться в [0,1]). Дополнительно создается классификационный признак. Разделить данные варианта на обучающую и тестирующую выборки. Персептрон. Так как персептрон способен делить объекты только на два класса, то организуем работу итерационно: Создать персептрон для отделения 1 класса от всех остальных. Протестировать персептрон по обучающей и тестирующей выборкам и определить процент правильно классифицированных объектов 1 класса. Создать персептрон для отделения 2 класса от оставшихся. Протестировать персептрон по обучающей и тестирующей выборкам и определить процент правильно классифицированных объектов 2 класса Продолжить, пока не будут разделены все объекты Построить графики разделяющей поверхности и визуальное представление результатов тестирования Для каждого вида сети (конкурирующая сеть, сеть распознавания, сеть с прямым распространением сигнала и обратным распространением ошибки) выполнить следующие этапы: 4.1 Создание сети 4.2 Обучение сети на обучающей выборке 4.3 Протестировать сеть отдельно по обучающей и по тестирующей выборке 4.4 Построить визуальное представление результатов тестирования 4.5 Оценить качество классификации в виде матриц 4.6 Выдать число итераций обучения Оформить результаты в виде таблицы
Вариант работы имеет вид:ZPM, где Z=1-6 – вид закона распределения генерируемых признаков Биномиальное Геометрическое Гипергеометрическое Пуассона Равномерное Нормальное P=2,3 – число признаков M=3,4,5 – число классов Нейронные сети. Архитектура нейронных сетей Идея нейронных сетей родилась в рамках теории искусственного интеллекта, в результате попыток имитировать способность биологических нервных систем обучаться и исправлять ошибки. Нейронные сети (Neural Networks) - это модели биологических нейронных сетей мозга, в которых нейроны имитируются относительно простыми, часто однотипными, элементами (искусственными нейронами). Нейронная сеть может быть представлена направленным графом с взвешенными связями, в котором искусственные нейроны являются вершинами, а синаптические связи - дугами. Нейронные сети широко используются для решения разнообразных задач. Среди областей применения нейронных сетей - автоматизация процессов распознавания образов, прогнозирование, адаптивное управление, создание экспертных систем, организация ассоциативной памяти, обработка аналоговых и цифровых сигналов, синтез и идентификация электронных цепей и систем. С помощью нейронных сетей можно, например, предсказывать объемы продаж изделий, показатели биржевого рынка, выполнять распознавание сигналов, конструировать самообучающиеся системы. Если говорить простым языком, многослойная нейронная сеть представляет собой совокупность нейронов, которые составляют слои. В каждом слое нейроны между собой никак не связаны, но связаны с нейронами предыдущего и следующего слоев. Информация поступает с первого на второй слой , со второго - на третий и т.д. Среди задач Data Mining, решаемых с помощью нейронных сетей, будем рассматривать такие: •Классификация (обучение с учителем). Примеры задач классификации: распознавание текста, распознавание речи, идентификация личности. •Прогнозирование. Для нейронной сети задача прогнозирования может быть поставлена таким образом: найти наилучшее приближение функции, заданной конечным набором входных значений (обучающих примеров). Например, нейронные сети позволяют решать задачу восстановления пропущенных значений. •Кластеризация (обучение без учителя). Примером задачи кластеризации может быть задача сжатия информации путем уменьшения размерности данных. Задачи кластеризации решаются, например, самоорганизующимися картами Кохонена Рассмотрим три примера задач, для решения которых возможно применение нейронных сетей. Медицинская диагностика. В ходе наблюдения за различными показателями состояния пациентов накоплена база данных. Риск наступления осложнений может соответствовать сложной нелинейной комбинации наблюдаемых переменных, которая обнаруживается с помощью нейросетевого моделирования. Прогнозирование показателей деятельности фирмы (объемы продаж). На основе ретроспективной информации о деятельности организации возможно определение объемов продаж на будущие периоды. Предоставление кредита. Используя базу данных о клиентах банка, применяя нейронные сети, можно установить группу клиентов, которые относятся к группе потенциальных неплательщиков. Элементы нейронных сетей Искусственный нейрон - элемент искусственных нейронных сетей, моделирующий некоторые функции биологического нейрона. Главная функция искусственного нейрона - формировать выходной сигнал в зависимости от сигналов, поступающих на его входы. В самой распространенной конфигурации входные сигналы обрабатываются адаптивным сумматором с учетом весов, затем выходной сигнал сумматора поступает на вход функции активации, и результат подается на выход. 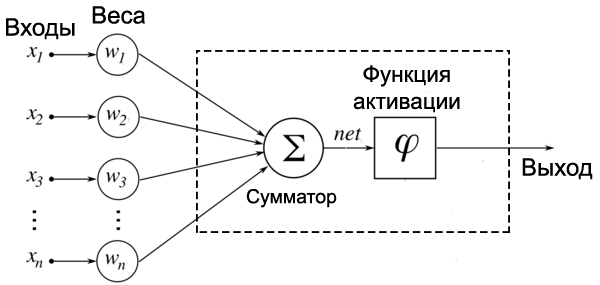 Ключевым в нейронных сетях является понятие слоя. Слой - один или несколько нейронов, на входы которых подается один и тот же общий сигнал. Однослойная сеть - сеть, состоящая из одного слоя. Многослойная сеть - сеть, имеющая несколько слоев. В многослойной сети первый слой называется входным, последующие - внутренними или скрытыми, последний слой - выходным. Число нейронов в каждом слое не связано с количеством нейронов в других слоях и может быть произвольным. В рамках одного слоя данные обрабатываются параллельно, а в масштабах всей сети обработка ведется последовательно - от слоя к слою. Нейронные сети могут обучаться с учителем или без него. При обучении с учителем для каждого обучающего входного примера требуется знание правильного ответа. Нейронной сети предъявляются значения входных и выходных сигналов, а она по определенному алгоритму подстраивает веса. В процессе обучения производится корректировка весов сети по результатам сравнения фактических выходных значений с выходными, известными заранее. В ходе обучения веса настраиваются таким образом, чтобы минимизировать разность между желаемым и полученным на выходе сигналами, которая называется ошибкой обучения. Из полученных разностей формируется функция ошибок. Часто используется сумма квадратов ошибок. При обучении без учителя раскрывается внутренняя структура данных или корреляции между примерами в наборе данных. Выходы нейронной сети формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные сигналы. В результате такого обучения примеры распределяются по категориям, сами категории и их количество могут быть заранее неизвестны. Алгоритм обучения нейронной сети является итеративным, его шаги называют эпохами или итерациями. 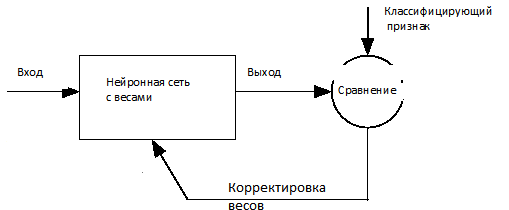 Эпоха включает предъявление всех примеров из обучающего множества. Сложность может вызвать вопрос о количестве наблюдений в наборе данных. И хотя существуют некие правила, описывающие связь между необходимым количеством наблюдений и размером сети, их верность не доказана. Количество необходимых наблюдений зависит от сложности решаемой задачи. При увеличении количества признаков количество наблюдений возрастает нелинейно. Нейронные сети могут быть синхронные и асинхронные. В синхронных нейронных сетях в каждый момент времени свое состояние меняет лишь один нейрон. В асинхронных - состояние меняется сразу у целой группы нейронов, как правило, у всего слоя. Ключевым в слоистых сетях является понятие слоя. Слой - один или несколько нейронов, на входы которых подается один и тот же общий сигнал. Многослойные нейронные сети - нейронные сети, в которых нейроны разбиты на отдельные группы (слои) так, что обработка информации осуществляется послойно. В многослойных сетях нейроны i-го слоя получают входные сигналы, преобразуют их и через точки ветвления передают нейронам (i+1) слоя. И так до k-го слоя, который выдает выходные сигналы для интерпретатора и пользователя. Число нейронов в каждом слое не связано с количеством нейронов в других слоях, может быть произвольным. В рамках одного слоя данные обрабатываются параллельно, а в масштабах всей сети обработка ведется последовательно - от слоя к слою. К слоистым нейронным сетям относятся, например, многослойные персептроны, сети радиальных базисных функций. Слоистые сети, в свою очередь, могут быть однослойными и многослойными. Однослойная сеть - сеть, состоящая из одного слоя. Многослойная сеть - сеть, имеющая несколько слоев. В многослойной сети первый слой называется входным, последующие - внутренними или скрытыми, последний слой - выходным. Таким образом, промежуточные слои - это все слои в многослойной нейронной сети, кроме входного и выходного. Входной слой сети реализует связь с входными данными, выходной - с выходными. Таким образом, нейроны могут быть входными, выходными и скрытыми. Входной слой организован из входных нейронов (input neuron), которые получают данные и распространяют их на входы нейронов скрытого слоя сети. Скрытый нейрон (hidden neuron) - это нейрон, находящийся в скрытом слое нейронной сети. Выходные нейроны (output neuron), из которых организован выходной слой сети, выдает результаты работы нейронной сети. Обучение нейронных сетей Перед использованием нейронной сети ее необходимо обучить. Процесс обучения нейронной сети заключается в подстройке ее внутренних параметров под конкретную задачу. Алгоритм работы нейронной сети является итеративным, его шаги называют эпохами или циклами. Эпоха - одна итерация в процессе обучения, включающая предъявление всех примеров из обучающего множества и, возможно, проверку качества обучения на контрольном множестве. Процесс обучения осуществляется на обучающей выборке. Обучающая выборка включает входные значения и соответствующие им выходные значения набора данных. В ходе обучения нейронная сеть находит некие зависимости выходных полей от входных. Аналитик должен определить количество слоев в сети и количество нейронов в каждом слое. Далее необходимо назначить такие значения весов и смещений, которые смогут минимизировать ошибку решения. Веса и смещения автоматически настраиваются таким образом, чтобы минимизировать разность между желаемым и полученным на выходе сигналами, которая называется ошибка обучения. Ошибка обучения для построенной нейронной сети вычисляется путем сравнения выходных и целевых (желаемых) значений. Из полученных разностей формируется функция ошибок Функция ошибок - это целевая функция, требующая минимизации в процессе управляемого обучения нейронной сети. С помощью функции ошибок можно оценить качество работы нейронной сети во время обучения. Например, часто используется сумма квадратов ошибок. От качества обучения нейронной сети зависит ее способность решать поставленные перед ней задачи. Виды нейронных сетей Персептрон Простейшая модель персептрона – это однослойная нейронная сеть, веса и смещения которой могут меняться в процессе обучения для последующего правильного распознавания входных векторов. Обучение персептрона осуществляется по определенным правилам. Простой нейрон с одним скалярным входом и без смещения показан на рисунке. 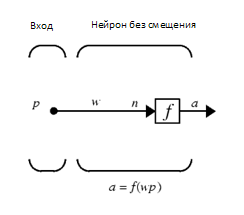 Скалярный вход p передается через соединение и умножается на скалярный вес w, образуя произведение n=wp, также скаляр. Взвешенный вход wp – единственный аргумент функции активации f, выходом которой является скаляр a. В персептроне используется пороговая функция активации (hardlim), которая дает на выходе или 0, если n меньше 0, или 1, если n больше или равно 0. 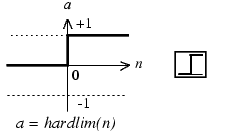 Нейрон на следующем рисунке имеет скалярное смещение b, которое добавляется к произведению wp. 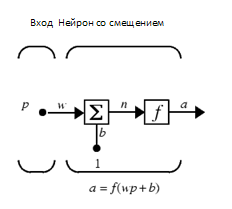 Нейрон с одним входным вектором из R элементов показан на следующем рисунке. Элементы вектора 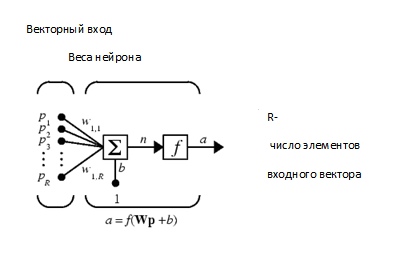 Персептрон показан на следующем рисунке. 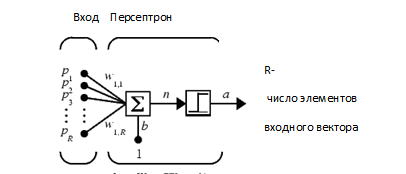 За счет функции передачи hardlimit персептрон обладает способностью классифицировать входные вектора путем деления входного пространства признаков на две области. Так, выход будет равен 0, если вход меньше 0, или 1, если вход больше или равен 0. Входное пространство персептрона с двумя входами, весами и смещением показано на рисунке. 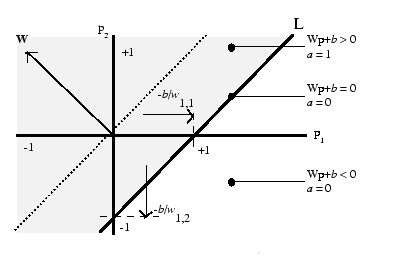 Две области классификации образуются с помощью разделяющей линии L на Wp+b=0. Эта линия перпендикулярна весовой матрице W и перемещается в соответствии со смещением b. Входные вектора над и слева от линии L будут соответствовать входным величинам больше 0 и поэтому за счет пороговой функции приведут к выходу, равному 1. Входные вектора ниже и правее линии L приведут к выходу, равному 0. Две области образуются с помощью разделяющей линии L на Wp+b=0 . Эта линия перпендикулярна весовой матрице W и перемещается в соответствии со смещением b. Входные вектора над линией L и слева от нее будут соответствовать входным величинам больше 0 и поэтому за счет пороговой функции приведут к выходу, равному 1. Входные вектора ниже и правее линии L приведут к выходу, равному 0. 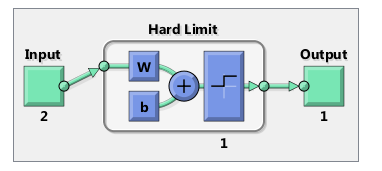 Рисунок 1 - Структура персептрона с двумя входами Конкурирующая сеть (сеть Кохонена)Это отдельный класс нейронных сетей, используемых для решения различных задач классификации. Каждый объект, который требуется классифицировать, представляется в виде некоторого вектора, подающегося на вход нейронной сети. Количество нейронов во входном слое определяется количеством признаков этого входного вектора. Количество же выходов определяется количеством классов, то есть если имеется M классов, то количество нейронов в выходном слое тоже будет M. Таким образом, каждый нейрон в выходном слое отвечает за свой класс. Значения, которые принимают нейроны в выходном слое, отображают, насколько вектор классифицируемого объекта на входе близок, по мнению нейронной сети Кохонена, к тому или иному классу. Чем больше «уверенность», что объект принадлежит к тому или иному классу, тем большее значение принимает нейрон соответствующего класса. Эту работу выполняет функция активации конкурирующей сети (softmax). Рассмотрим следующую нейронную сеть Кохонена с n входами и r выходами, т.е. нейронную сеть для классификации по r классам 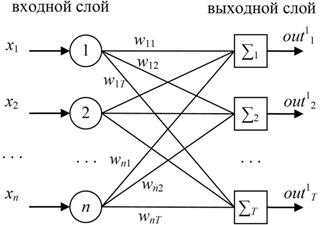 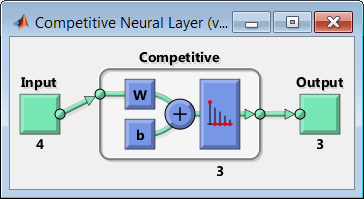 Рисунок 2 - Структура слоя Кохонена с четырьмя входами и тремя выходами Нейронная сеть для распознавания. Это двухслойная сеть, в которой вход связан со скрытым слоем с сигмоидной функцией активации, выходы которого передаются на выходной слой с функцией активации конкурирующей сети. 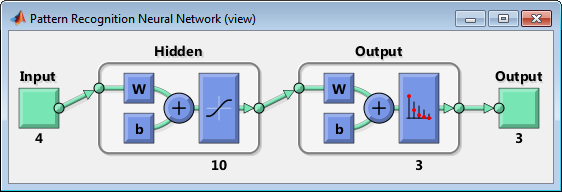 Рисунок 3 - Структура сети распознавания образов с четырьмя входами и тремя выходами Сеть прямого распространения сигнала Такая сеть имеет одностороннее соединение от входных до выходных слоев. Функция активации для скрытого слоя tansig (гиперболический тангенс) и для выходного слоя purelin (линейная функция). 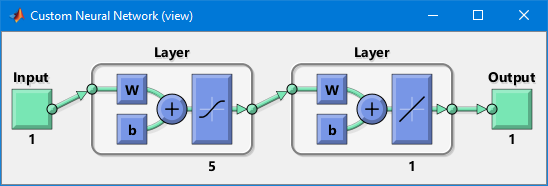 Рисунок 3 - Структура сети прямого распространения сигнала с одним входом Персептрон Создание персептрона net= Perceptron(n_iters=1000) Входной аргумент: n_iters – число эпох обучения. Выходной аргумент: net – структура, содержащая информацию о персептроне. class Perceptron: def __init__(self, learning_rate=0.01, n_iters=1000): self.lr = learning_rate self.n_iters = n_iters self.aclivation_func = self._unit_step_func self.weights = None self.bias = None def fit(self, X, y): n_samples, n_features = X.shape self.weights = np.zeros(n_features) self.bias = 0 y_ = np.array([1 if i > 0 else 0 for i in y]) for _ in range(self.n_iters): for idx, x_i in enumerate(X): linear_output = np.dot(x_i, self.weights) + self.bias y_predicted = self.aclivation_func(linear_output) update = self.lr * (y_[idx] - y_predicted) self.weights += update * x_i self.bias += update def predict(self, X): linear_output = np.dot(X, self.weights) + self.bias y_predicted = self.aclivation_func(linear_output) return y_predicted #функция активации (если результат сумматора >= 0, то результат = 1) def _unit_step_func(self, x): return np.where(x>=0, 1, 0) Обучение нейронной сети net.fit(X_train, Y_train) Входные аргументы: X_train - входы - матрица RхQ из Q входных векторов обучающего множества – столбцов размерности R каждый (R-количество признаков). Y_train - целевые значения - вектор из Q значений (значения 0 или 1) Выход: net - структурированная и обученная сеть Для получения выходных значений по обученной сети можно использовать функцию predict: выход = net.predict(P) P - вход - матрица RхQ из Q входных векторов обучающей или тестирующей матрицы – столбцов размерности R каждый (R-количество признаков). Выход – вектор из 0 или 1 результатов, полученных по обучающей сети Вывод обучающей выборки с окраской отделенного персептроном класса prY_Train = net.predict(X_train) plt.figure(figsize=(16,8)) plt.scatter(X_train[:,0], X_train[:,1], marker='o', linewidths=1, c= prY_Train) plt.grid() #построение разделяющей прямой по весам и смещениям x0_1 = np.amin(X_train[:,0]) x0_2 = np.amax(X_train[:,0]) x1_1 = (-net.weights[0] * x0_1 - net.bias) / net.weights[1] x1_2 = (-net.weights[0] * x0_2 - net.bias) /net.weights[1] #добавление прямой на график plt.plot([x0_1, x0_2], [x1_1, x1_2]) 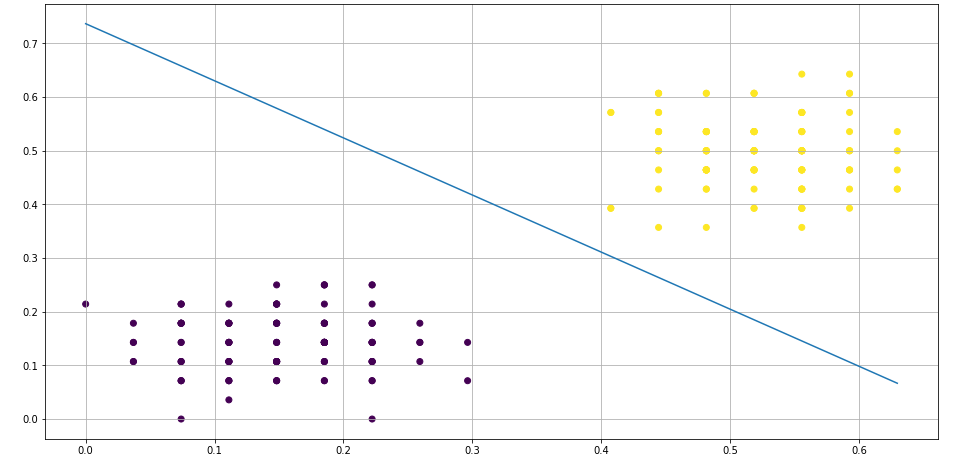 #матрица различий r = confusion_matrix(Y_train, prY_Train) print(r) Пример вычисления матрицы confusion C_t = confusionmat(Y,Y_t); 0 0 50 48 2 0 14 36 0 Исходя из этого, можно сказать, что 50 объектов 1 класса отнесены алгоритмом к 3 классу, 48 объектов 2 класса отнесены алгоритмом к 1 классу, 36 объектов 2 класса отнесены алгоритмом ко 2 класса. Конкурирующая сеть (Кохонена) Создание сети net = KohonenNet(m=3, n=1, weights=weights) class KohonenNet(): def __init__(self, m=3, n=3, lr=1, sigma=1, max_iter=3000, weights = []): self.m = m #количество классов self.n = n #количество уровней сети self.shape = (m, n) self.initial_lr = lr self.lr = lr #скорость обучения self.sigma = sigma #параметр изменения скорости обучения (она будет снижаться с каждой итерацией) self.max_iter = max_iter self.weights = weights #функция нахождения выйгравшего нейрона (нейрона с минимальным расстоянием до точки) def _find_bmu(self, x): x_stack = np.stack([x]*(self.m*self.n), axis=0)#матрица размером [количество центров кластеров(нейронов), количество признаков] (для каждого веса своя строка признаков(точка)) distance = np.linalg.norm(x_stack - self.weights, axis=1)#эвклидовы расстояния между точкой выборки и нейронами return np.argmin(distance)#возвращаем индекс минимального расстояния (индекс подходящего нейрона) def step(self, x): x_stack = np.stack([x]*(self.m*self.n), axis=0)#матрица размером [количество весов, количество признаков] (для каждого веса своя строка признаков(точка)) bmu_index = self._find_bmu(x)#передаем в функцию строку признаков (точку) и получаем индекс выйгравшего нейрона (центра кластера) self.weights[bmu_index] += self.lr * (x - self.weights[bmu_index]) #обучение весов def fit(self, X, epochs=1, shuffle=True): global_iter_counter = 0 n_samples = X.shape[0]#количество элементов выборки total_iterations = np.minimum(epochs * n_samples, self.max_iter)#количество обучения весов в эпохе for epoch in range(epochs):#изначально у нас 1 эпоха if global_iter_counter > self.max_iter:#не даем проводить больше 3000 эпох break if shuffle: indices = np.random.permutation(n_samples)#создание массива с индексами в разброс else: indices = np.arange(n_samples)#создание массива с индексами по порядку #обучение for idx in indices:#проход по выборке с индексами idx if global_iter_counter > self.max_iter: break input = X[idx] #перемещение нейрона(изменение весов победившего нейрона) self.step(input) global_iter_counter += 1 self.lr = (1 - (global_iter_counter / total_iterations)) * self.initial_lr#изменение параметра обучения self._n_iter_ = global_iter_counter return def returnChangedWeights(self): return self.weights def predict(self, X): labels = np.array([self._find_bmu(x) for x in X]) return labels Обучение нейронной сети net.fit(X_train, shuffle=True) Для получения выходных значений по обученной сети можно использовать функцию predict: выход = net.predict(P) P - вход - матрица RхQ из Q входных векторов обучающей или тестирующей матрицы – столбцов размерности R каждый (R-количество признаков). Выход – вектор меток для классифицированных объектов, полученных по обучающей сети 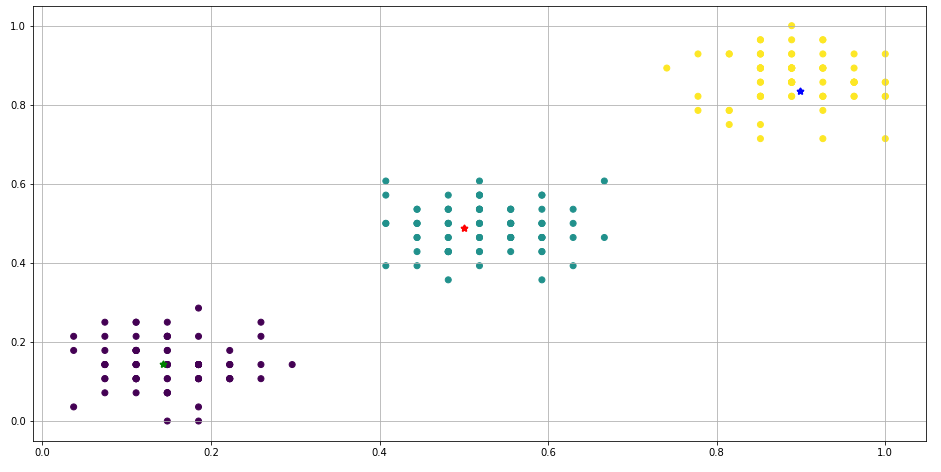 Нейронная сеть для распознавания !pip install neupy from neupy import algorithms pnn = algorithms.PNN(std=10, verbose=False) pnn.train(X_train, Y_train) prY_Train = pnn.predict(X_train) print(prY_Train) r = confusion_matrix(Y _train, prY_Train) print(r) plt.figure(figsize=(16,8)) plt.scatter(X_train[:,0], X_train[:,1], marker='o', linewidths=1, c= prY_Train) plt.grid() 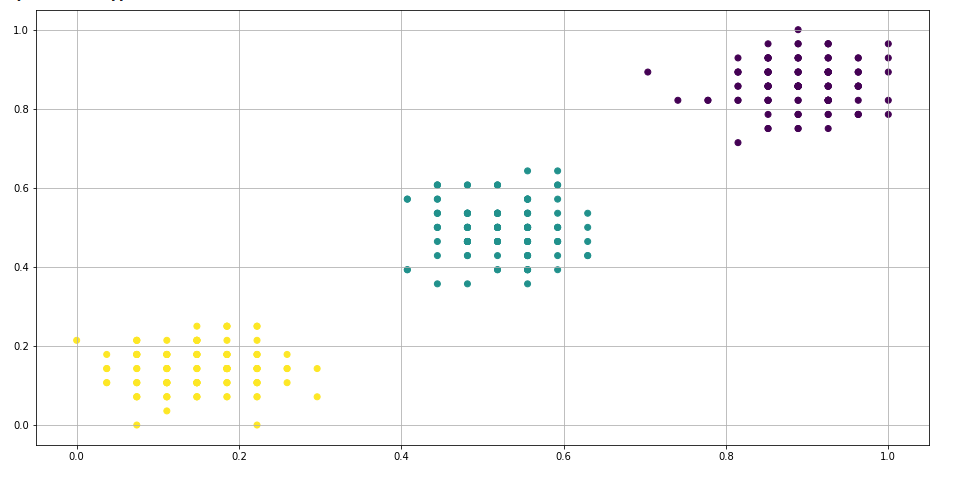 prY_Test = pnn.predict(X_test) print(prY_Test) r = confusion_matrix(Y _test, prY_Test) print(r) plt.figure(figsize=(16,8)) plt.scatter(X_test[:,0], X_test[:,1], marker='o', linewidths=1, c= prY_Test) plt.grid() 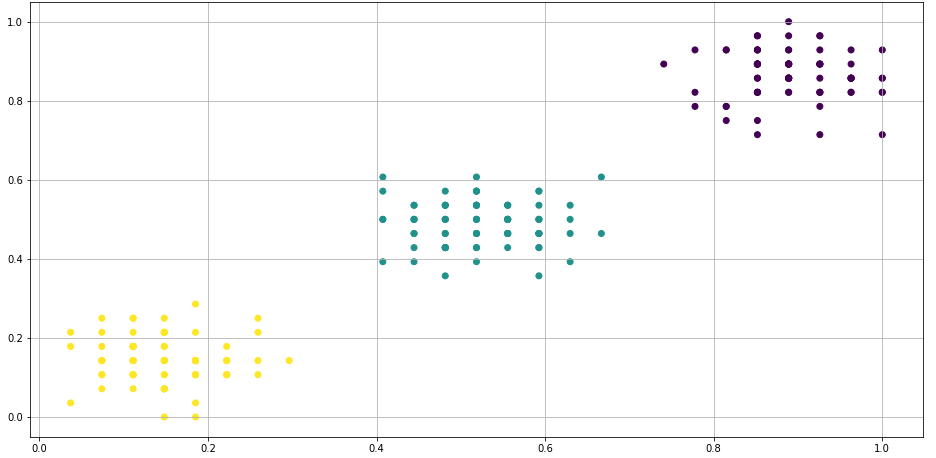 Сеть прямого распространения сигнала и обратного распространения ошибки Для создания и обучения двухслойной сети прямого распространения сигнала, представленной выше, где функция активации для скрытого слоя - гиперболический тангенс, а для выходного слоя - линейная функция, можно воспользоваться статьей: How to Code a Neural Network with Backpropagation In Python (from scratch) // Machine Learning Mastery URL: https://machinelearningmastery.com/implement-backpropagation-algorithm-scratch-python/ (дата обращения: 15.10.2021). Предсказание значений классифицирующего признака по обученной сети blist = X_train.tolist() Y_train=y_train-1 Y_train= Y_train.tolist() for i in range(0, len(y_train)): blist[i]=blist[i]+Y_train[i] print(blist) dataset=blist n_inputs = len(dataset[0]) - 1 n_outputs = len(set([row[-1] for row in dataset])) network = initialize_network(n_inputs, 2, n_outputs) train_network(network, dataset, 0.5, 200, n_outputs) # # Make a prediction with a network def predict(network, row): outputs = forward_propagate(network, row) return outputs.index(max(outputs)) i=-1 for row in dataset: i=i+1 prediction = predict(network, row) if (i==0): predictTrain = np.array([[prediction]]) else: predictTrain =np.append(predictTrain,[[prediction]],axis=0) print(confusion_matrix(Y_train, predictTrain)) i=-1 for row in X_test: i=i+1 prediction = predict(network, row) if (i==0): predictTest = np.array([[prediction]]) else: predictTest =np.append(predictTest,[[prediction]],axis=0) print(confusion_matrix(y_test-1, predictTest)) Контрольные вопросы Перечислите, из каких элементов состоит нейронная сеть. Что такое пороговая функция активации и в каком типе нейронной сети она используется? Какова особенность нейронной сети типа персептрон? Что такое конкурирующая функция активации и в каком типе нейронной сети она используется? В чем смысл обучения нейронной сети? Назовите алгоритмы обучения в реализованных ИНС. Как определяется число нейронов в слоях многослойной сети? Как оценивается качество классификации/кластеризации в данной лабораторной работе? Исследуйте влияние структуры сети распознавания образов на точность распознавания и число циклов обучения. |
