Лабораторная работа № 1.
Программирование циклическихалгоритмов
Цель лабораторной работы.
Закрепление теоретических знаний по основам применения операторов if,else и switch.
Задание на лабораторную работу:
Для указанного преподавателем варианта написать на языке C# в среде Microsoft Visual Studio соответствующие программы. В таблице 3 для каждого варианта указаны задания из таблицы 1 и 2, которые необходимо выполнить на лабораторной работе.
Задания выполнить в одном проекте, либо в двух (табл. 1 и табл. 2)
Табл. 1. Задания на применение циклических операторов
1
|
На промежутке от 1 до M найти все числа Армстронга. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу.
|
2
|
Дано натуральное n. Вычислить: 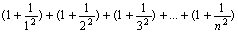
|
3
|
Дано натуральное n. Вычислить: 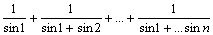
|
4
|
Дано действительное число х, натуральное число n. Вычислить:
x ( x - n )( x - 2 n )( x - 3 n )…( x - n2 );
|
5
|
Дано действительное число х, натуральное число n. Вычислить: 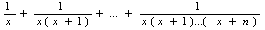
|
6
|
Дано действительное число х, натуральное число n. Вычислить: 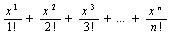
|
7
|
Дано натуральное n. Вычиcлить: 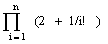
|
8
|
Дано натуральное n. Вычиcлить: 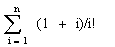
|
9
|
Вычислить приближенно значение бесконечной суммы (справа от каждой суммы дается ее точное значение, с которым можно сравнить полученный ответ): 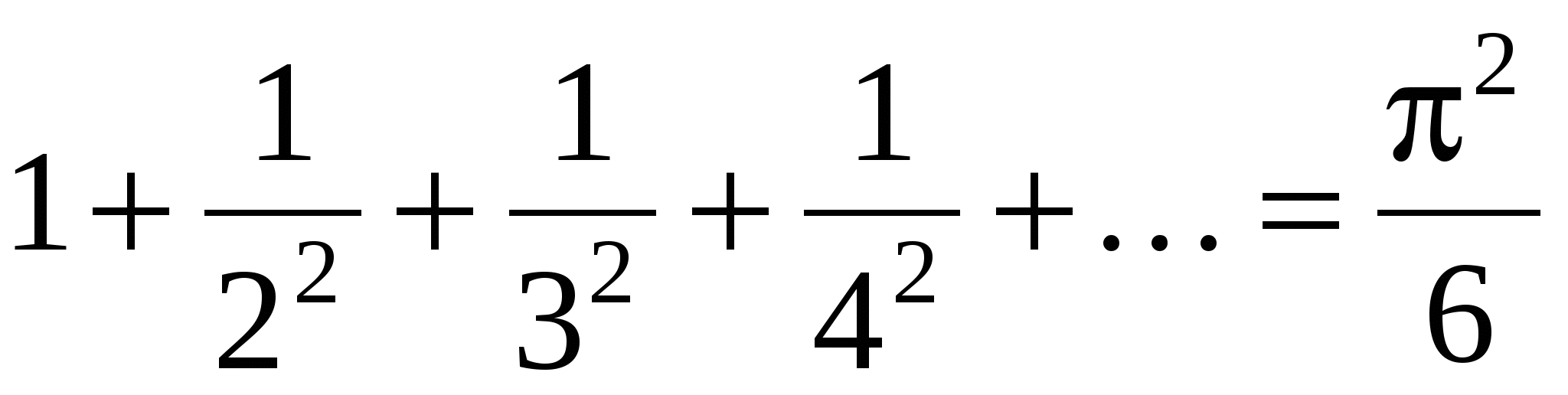
|
10
|
Вычислить приближенно значение бесконечной суммы (справа от каждой суммы дается ее точное значение, с которым можно сравнить полученный ответ): 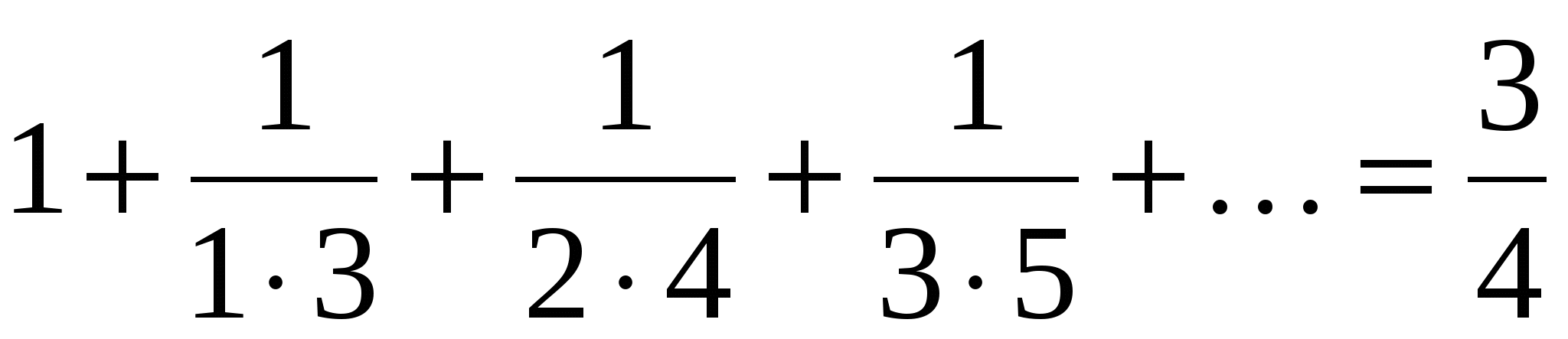
|
11
|
Вычислить приближенно значение бесконечной суммы (справа от каждой суммы дается ее точное значение, с которым можно сравнить полученный ответ): 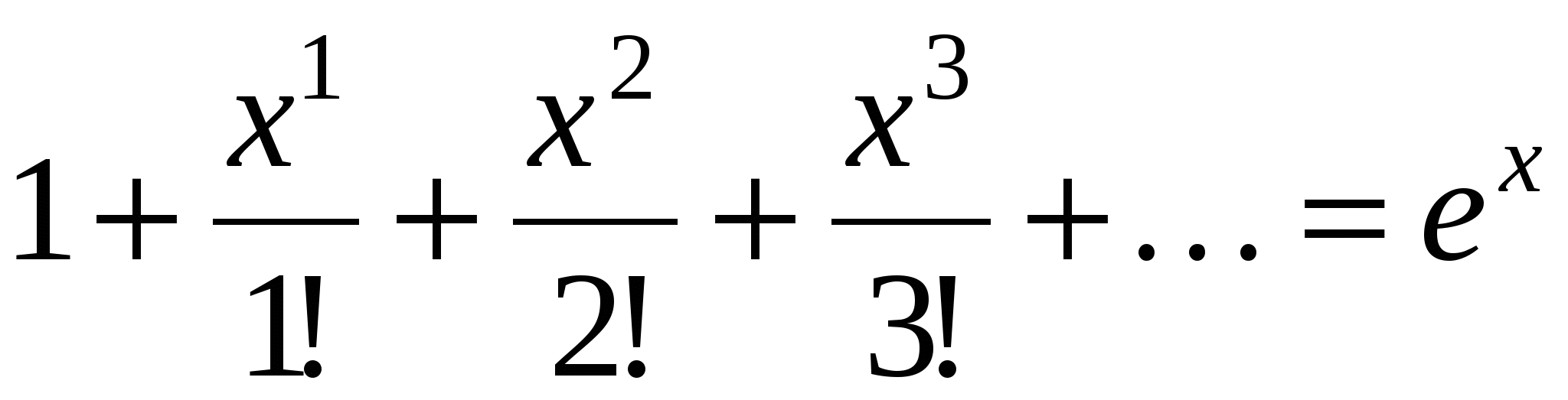
|
Табл. 2. Задания на применение циклических операторов
1
|
Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2,3,4,5,6,7,8,9.
|
2
|
Найти все трехзначные числа, сумма цифр которых равна данному целому числу.
|
3
|
Найти все трехзначные числа, средняя цифра которых равна сумме первой и второй цифр.
|
4
|
Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры.
|
5
|
Найти все двузначные числа, сумма квадратов цифр которых делится на 17.
|
6
|
Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр.
|
7
|
Найти двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа.
|
8
|
Найти двузначное число, равное утроенному произведению его цифр.
|
9
|
В каких двузначных числах удвоенная сумма цифр равна их произведению?
|
10
|
Можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел? Написать программу решения этой задачи.
|
11
|
Определить, является ли заданное число совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3).
|
12
|
Для заданного натурального числа 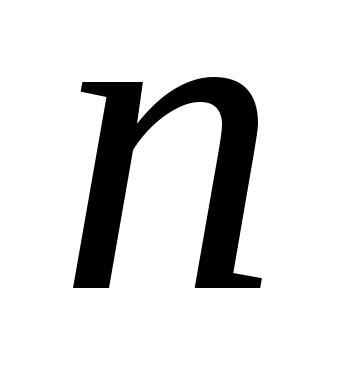 и действительных чисел и действительных чисел 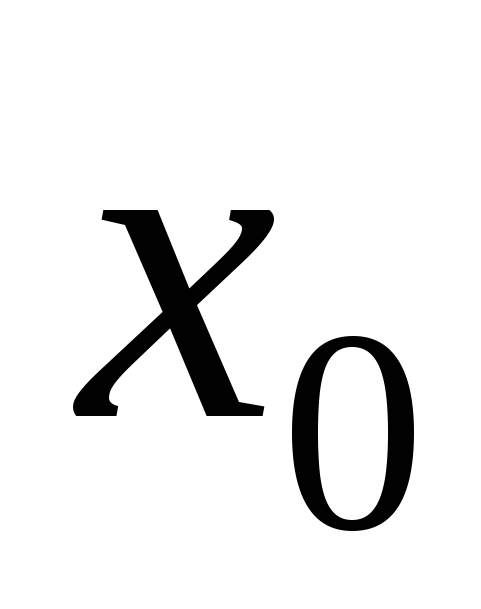 и и  вычислить вычислить 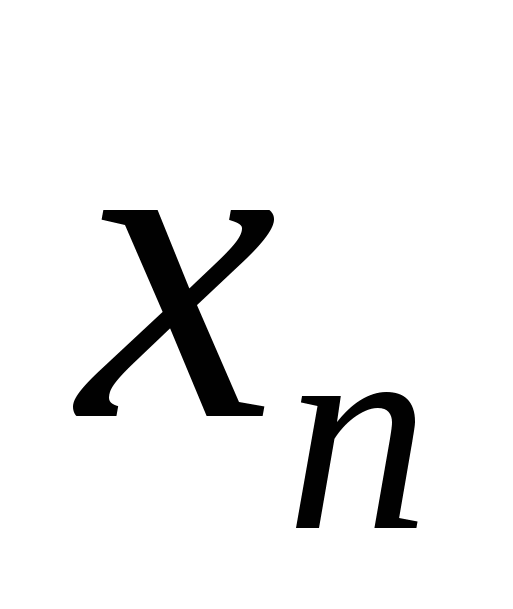 , по итерационной формуле: , по итерационной формуле: 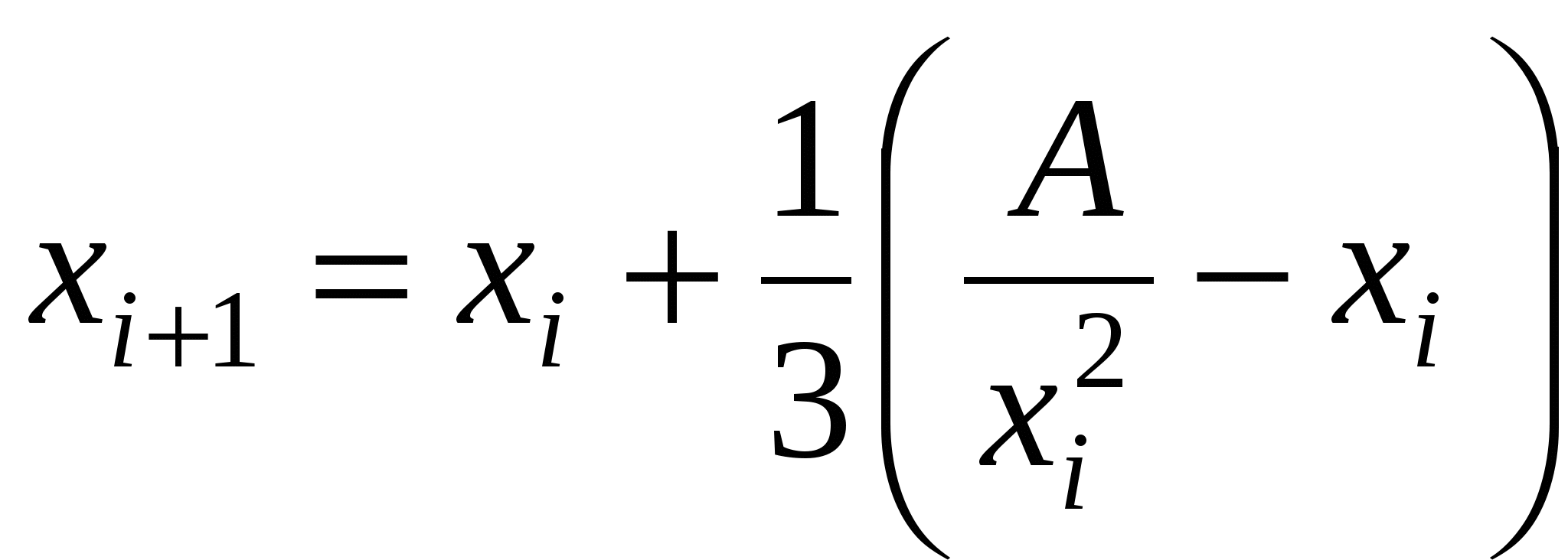 . .
|
Табл. 3. Варианты заданий на лабораторную работу
1
|
№ 3, № 7, № 11 из табл. 1 и №8, №1, № 6 из табл. 2
|
2
|
№ 4, № 8, № 1 из табл. 1 и №9, №2, № 7 из табл. 2
|
3
|
№ 5, № 9, № 2 из табл. 1 и №10, №3, № 8 из табл. 2
|
4
|
№ 6, № 10, № 3 из табл. 1 и №11, №4, № 9 из табл. 2
|
5
|
№ 7, № 11, № 4 из табл. 1 и №12, №5, № 10 из табл. 2
|
6
|
№ 8, № 1, № 5 из табл. 1 и №1, №6, № 11 из табл. 2
|
7
|
№ 9, № 2, № 6 из табл. 1 и №2, №7, № 12 из табл. 2
|
8
|
№ 10, № 3, № 7 из табл. 1 и №3, №8, № 1 из табл. 2
|
9
|
№ 11, № 4, № 8 из табл. 1 и №4, №9, № 2 из табл. 2
|
10
|
№ 1, № 5, № 9 из табл. 1 и №5, №10, № 3 из табл. 2
|
11
|
№ 7, № 9, № 11 из табл. 1 и №6, №3, № 9 из табл. 2
|
12
|
№ 4, № 2, № 8 из табл. 1 и №1, №6, № 12 из табл. 2
| |
 Скачать 74 Kb.
Скачать 74 Kb.