Лабораторная работа работа с картой масштабы, координаты, углы ориентирования

• Название: Лабораторная работа работа с картой масштабы, координаты, углы ориентирования
• Дата: 23.03.2023
• Размер: 1.26 Mb.
• Имя файла: lab.rab_geod_1,2_semestr_1649640874.doc
• Тип: Лабораторная работа; #1010021
• страница: 2 из 3

Румбом направления r называют острый угол в пределах 90 град. в одной из четвертей между ближайшим северным или южным концом осевого меридиана (вертикальной линией сетки ) и данным направлением.

Взаимосвязь румбов, дирекционных углов и приращений координат (приращение координат – разница между координатами вершин конечной и начальной точки направления)показана на рис. 2., табл.1.

Таблица 1.

Взаимосвязь румбов, дирекционных углов и приращений координат

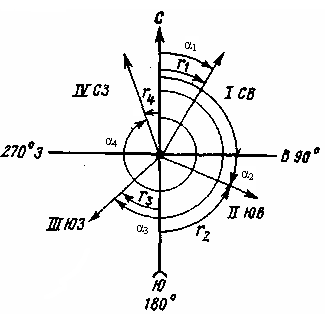Приращения координат	Дирекционный угол
	α1= r	α4=180° — r	α3 = 180°+r	α4 = 360° — r
	Румб
	r=α	r=180°-α	r= α-180°	r=360°-α
Δy	+	+	-	-
Δх	+	-	-	+
Четверть	I (СВ) 0—90°	II (ЮВ) 90—180°	III (ЮЗ) 180—270	IV (CЗ) 270 -360°

Рис.1. Взаимосвязь румбов и дирекционных углов
Задание 1.

Таблица 2.

Номер п.п.	Дирекционный угол α	Четверть	Формула	Румб r
1	278°25'
2	30°58'
3	115°20'
4	225°40'

Задание 2.

Таблица 3.

Номер п.п.	Румб r	Четверть	Формула	Дирекционный угол α
1	78°26'	СВ
2	30°28'	II
3	17°18'	ЮЗ
4	11°14'	IV
5	25°50'	ЮВ
6	35°07'	III

Задание 3.
α_1-2 = α_2-1 =

r_1-2=
r_1-2= r_2-1 =
Задание 4. Дирекционный угол α_1-2 направления 1-2 определяется в следующем порядке:

• 
  Определяем приращения координат по формулам
  

• 
  Определяем румб направления 1-2:
  

Определяем дирекционный угол α_1-2 направления по одной из формул таблицы 1 в соответствии со знаками приращений координат:

α_1-2=

2 семестр (экзамен)
Лабораторные работы № 1-5. ОПРЕДЕЛЕНИЕ ПЛОЩАДИ

Цель работы: - ознакомиться с различными способами определения площадей.

Материалы, приборы и принадлежности – топографический план, калька, планиметр, чертежные инструменты, калькулятор.

Задание: Построить контур полигона (см. табл.) по координатам вершин участка в масштабе 1:25000. Вычислить площадь замкнутого полигона способами: линейной палеткой, квадратной палеткой, геометрическими фигурами, аналитическим. Произвести оценку точности.

Основные понятия и формулы

Определение площади аналитическим способом

Если по результатам измерений на плане (карте) определены координаты вершин замкнутого многоугольника, то площадь последнего может быть определена аналитическим способом по формуле

или

Для контроля вычисления производят по обеим формулам.

Результаты записываются в ведомость вычисления площадей:

Вершины	Координаты		Разности координат		Произведения
	X, м	Y, м	Xi-1 - Xi+1	Yi+1 – Yi-1	Yi (Xi-1 - Xi+1) (4)∙(3)	Xi (Yi+1 – Yi-1) (5)∙(2)
1	2	3	4	5	6	7
1	5957700	12304275
2	5958500	12304650
3	5958375	12306500
4	5957475	12306600
5	5956725	12305350
Σ			0.0	0.0	2S =	2S =
					S= м2
					S= Га

Определение площади графическим способом

Сущность графического способа состоит в том, что площадь участка на плане разбивается на простейшие геометрические фигуры - прямоугольники трапеции, треугольники. По формулам геометрии определяют площади отдельных фигур и подсчитывают общую площадь участка. Наилучшим вариантом разбивки является деление участка на равносторонние треугольники. Точность определения площади участка зависит от числа взятых фигур и углов границы участка. Точность измерения повышается в результате повторных измерений и при новой разбивке участка на другие фигуры. За окончательный результат принимают среднее арифметическое из всех измерений.

Примечание: При расчетах линейные размеры фигур использовать в метрах местности, т.е. при масштабе 1: 25 000, 1 мм плана соответствует 25 м местности.

Квадратная палетка (рис. а).

Как правило, конфигурации участков леса, пашен, лугов, болот и т.д. имеют неправильные геометрические формы. Поэтому для измерения площадей небольших участков с криволинейным контуром применяют квадратные или параллельные палетки на прозрачном материале (рис. а, б).

Квадратная палетка представляет собой сеть квадратов со стороной 5 мм,

Площадь одного квадрата Sкв определится:

Sкв =(dкв)²

гдеdкв – длина стороны квадрата палетки в масштабе местности, м.

Например, для масштаба плана 1:1000, dкв=50м, 1:500 – 25 м, 1:25000 – 125 м и т.д.

Площадь участка определяется подсчетом числа целых квадратов n1 и половинок квадратов n2, заключенных в фигуре участка. Для повышения точности и контроля измерение площади участка следует производить повторно, меняя положение палетки относительно контура участка.

Общая площадь участка Sбудет равна:

S = Sкв (n1+n2/2)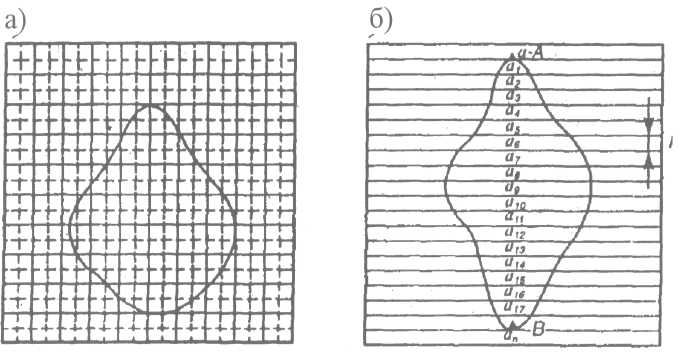



Рис. Палетки: а - квадратная; б – параллельная

Линейная палетка (рис.б). Здесь параллельные линии проведены на расстоянии 5 мм одна от другой. Палетку накладывают на криволинейный контур участка так, чтобы какие-нибудь две линии палетки касались контура (А и В). В этом случае можно считать, что площадь участка разбивается палеткой на ряд трапеций с основаниями ai,a₂, .., а_пи постоянной высотой h.

Крайние части палетки с точками А и В следует считать трапециями с основаниями, равными нулю. Общая площадь участка Sбудет равна:

S = h (a₁+ a₂+ ...+ a_n)
Оценка точности определения площади участка

№	Метод определения площади	Площадь S(уч)i, га	ΔSi, га	Масштаб топокарты
1	Линейная палетка			1:25 000
2	Квадратная палетка			1:25 000
3	Геометрические фигуры			1:25 000
4	Аналитический			1:25 000
		ΣSуч=

1. Среднее арифметическое значение площади участка

2. Отклонение каждого метода от Sср:

3. Определение ошибки вычисления площади



4. Относительная ошибка определения площади



5.Допустимая ошибка определения площади



где - графическая точность измерений; М-знаменатель численного масштаба топокарты

6. Контроль:

Лабораторная работа № 6