Лабораторная работа Транспортная задача_учет пропускной способно. Лабораторная работа Решение задач транспортного типа в Excel с учетом пропускной способности и с дополнительными ограничениями
 Скачать 134.2 Kb. Скачать 134.2 Kb.
|
|
Лабораторная работа № Решение задач транспортного типа в Excel с учетом пропускной способности и с дополнительными ограничениями. Особенностью этой модели является равенство суммарного объема продукции у поставщиков суммарному спросу потребителей, т.е.: 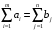 . . Такие задачи о перевозках называются задачами закрытого типа. На практике редки случаи равенства суммарного спроса потребителей и объемов запасов продукции у поставщиков. Если условие не соблюдается, то такие задачи называют задачами открытого типа. Для решения их предварительно преобразовывают к закрытому типу. Возможны два случая: а) суммарный объем продукции у поставщиков больше суммарного спроса потребителей, т.е. 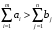 ; ;б) суммарный объем продукции у поставщиков меньше суммарного спроса потребителей, т.е. 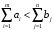 . . Для преобразования открытой задачи в закрытый тип в первом случае вводят фиктивного потребителя (m+1) со спросом 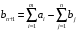 , во втором случае вводят фиктивного поставщика (n+1) с объемом поставок , во втором случае вводят фиктивного поставщика (n+1) с объемом поставок 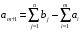 . . Методику преобразования открытой задачи к закрытому типу иллюстрируют нижеприведенные таблицы для случая, когда объем продукции у поставщиков больше спроса потребителей. Пример 1. Пусть имеется три поставщика продукции одного и того же вида и четыре потребителя этой продукции. Объем продукции у поставщиков, спрос потребителей и затраты на перевозку единицы продукции по каждому маршруту приведены в таблице 1. Требуется составить оптимальный план перевозки продукции, позволяющий минимизировать суммарные затраты на перевозку. Таблица 1 Транспортная задача открытого типа
Таблица 2 Методика преобразования открытой задачи к закрытому типу
Табличная запись задачи в MS Excel для решения с помощью инструментария «Поиск решения», представлена на рис.1 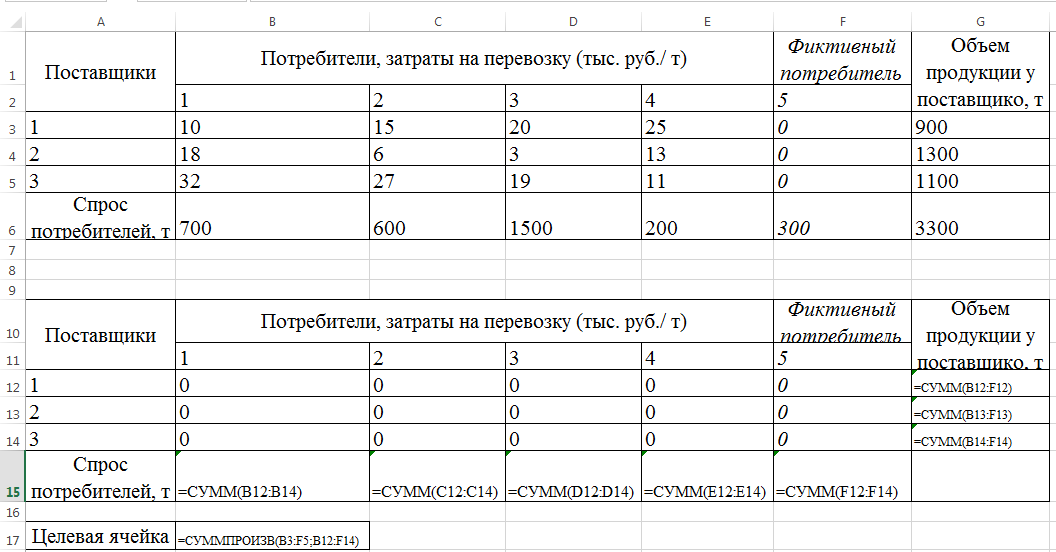 Рис.1 Табличная запись задачи в MS Excel На практике часто возникают ситуации, когда перевозки продукции по отдельным маршрутам не целесообразны или ограничены. В таких случаях условия неотрицательности переменных следует заменить неравенствами вида 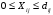 , , 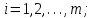 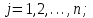 где dij- максимальное число единиц продукции, которое может быть перевезено из пункта 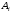 в пункт в пункт 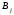 . Сформулированная задача называется транспортной задачей с ограниченными пропускными способностями. Она может быть сведена к обычной транспортной задаче. Методика включения в модель таких ситуаций получила название «Учет пропускной способности в моделях транспортного типа». . Сформулированная задача называется транспортной задачей с ограниченными пропускными способностями. Она может быть сведена к обычной транспортной задаче. Методика включения в модель таких ситуаций получила название «Учет пропускной способности в моделях транспортного типа».Чтобы исключить перевозку по какому-либо маршруту, достаточно численное значение критерия оптимальности по этому маршруту принять значительно большим, чем по остальным маршрутам, если задача решается на минимум и значительно меньшим, если задача решается на максимум. Остановимся на второй ситуации, которая более распространена на практике, и учет которой более сложен. Рассмотрим пример. Пусть в выше рассмотренной задаче о перевозках продукции от трех поставщиков четырем потребителям по маршруту 23 (от второго ростовщика третьему потребителю) можно перевезти не более 800 т. продукции. Методика учета ограничения по пропускной способности показана на следующей таблице Таблица 3 Методика учета ограничения по пропускной способности транспортной задачи
Решить задачи транспортного типа с помощью инструментария «Поиск решения» MS Excel (таблица 2, таблица 3). Ранее рассматривались транспортные задачи, в которых необходимо было перевезти какой-то однородный продукт. Если продуктов необходимых для перевозки несколько, такую задачу можно решить двумя способами: 1. Сформировать по каждому виду перевозимых продуктов свою транспортную задачу (однопродуктовую). Частные решения этих задач и будут представлять оптимальный план перевозок. 2. Сформировать одну (многопродуктовую) транспортную задачу. Рассмотрим методику формулировки многопродуктовой транспортной задачи на следующем примере. Пример 2. Для трех пользователей необходимо пополнить запасы бензина АИ-76 и АИ-93. Пополнение запасов может производиться из хранилища города Махачкалы и Избербаша. Запасы и потребности бензина представлены в табл. 5 и 5.
Протяженность маршрутов представлена в табл. 6. Таблица 6.
В целях упрощения вычислений предположим, что 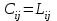 , где , где 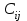 - стоимость перевозки между пунктами i и j; - стоимость перевозки между пунктами i и j; 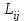 - протяженность маршрута между пунктами i и j. - протяженность маршрута между пунктами i и j.Для того чтобы учесть многопродуктовый характер задачи, сформируем транспортную модель следующим образом. Вместо того чтобы рассматривать каждого поставщика как один исходный пункт, разобьем его на несколько пунктов в соответствии с количеством видов перевозимых горюче-смазочных материалов (ГСМ). Аналогично поступим и с пунктами назначения (потребителями). В результате для нашего примера получим 4 поставщика и 5 потребителей (рис. 1). 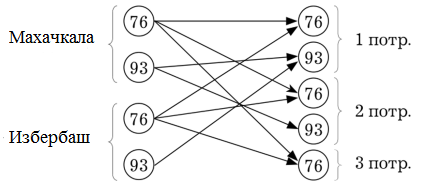 Рис. 1. Схема реализации многопродуктовой задачи Заметим, что некоторые маршруты недопустимы, поскольку в данной постановке задачи не допускается взаимная компенсация различных марок бензина. Это необходимо учесть при построении транспортной таблицы, а именно запрещенным маршрутам приписывают очень высокую стоимость перевозки. Транспортная таблица для многопродуктовой транспортной задачи в условиях нашего примера имеет следующий вид (табл. 7): Таблица 7. Многопродуктовая транспортная задача
1000 — недопустимые маршруты Данную транспортную таблицу можно разбить на несколько таблиц по видам продуктов (в нашем случае на две). Следует заметить, что с вычислительной точки зрения небольшие подзадачи решать проще, чем одну сложную. Но разбиение многопродуктовой модели на однопродуктовые можно осуществлять только в том случае, если нет взаимной связи между отдельными видами продуктов. Если такая связь существует, то многопродуктовую модель не удается столь просто разбить на однопродуктовые. Пример 3. В условиях предыдущего примера предположим, что в 1 потр. возможна взаимная компенсация АИ-76 и АИ-93 на 10%, во 2 потр. — на 20%. При построении транспортной таблицы необходимо в 1-й и 2-й потр. добавить по одному потребителю, величины спроса которых определим из данных о процентном соотношении заменяемых видов ГСМ. 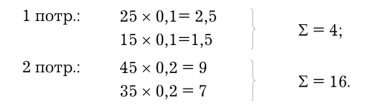 I -— сумма спросов первого и второго потребителей. Далее необходимо сформировать транспортную таблицу следующего вида (табл. 8): Таблица 8. Многопродуктовая транспортная задача с взаимосвязанными продуктами
Задачи для самостоятельного решения Задача 1. На трех ж/д станциях А1, А2, А3 скопилось 120, 110 и 130 незагруженных вагонов. Эти вагоны необходимо наиболее экономичным способом переправить на 5 других станций В1, В2, В3, В4, В5, потребность в вагонах на которых равна 80, 60, 70, 100, 50 соответственно. С А2 не представляется возможным переправить вагоны на В2 и В4. Тарифы перевозки вагонов заданы в таблице 9. Таблица 9 Тарифы перевозки вагонов
Найти оптимальный план переправки вагонов. Задача 2. Поставщики товара - оптовые коммерческие предприятия 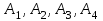 имеют запасы товаров соответственно в количестве 225, 250, 125, 100 ед. и розничные торговые предприятия имеют запасы товаров соответственно в количестве 225, 250, 125, 100 ед. и розничные торговые предприятия 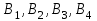 - подали заявки на закупку товаров в объемах соответственно: 120, 150, 110, 235 ед. Тарифы перевозок единицы груза с каждого из пунктов поставки в соответствующие пункты потребления заданы в виде матрицы . - подали заявки на закупку товаров в объемах соответственно: 120, 150, 110, 235 ед. Тарифы перевозок единицы груза с каждого из пунктов поставки в соответствующие пункты потребления заданы в виде матрицы . 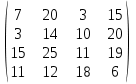 Найти такой план перевозки груза от поставщиков к потребителям, чтобы совокупные затраты на перевозку были минимальными. Задача 3. Решить транспортную задачу, исходные данные которой приведены в табл. 10, при дополнительных условиях: а) объем перевозки от четвертого поставщика первому потребителю должен быть не более 100 ед. б) объем перевозки от третьего поставщика третьему потребителю должен быть не менее 50 ед. Таблица 10.
Задача 4. Строительный песок добывается в трех карьерах с производительностью в день 46, 34 и 40 т. соответственно. Затраты на добычу одной тонны песка составляют 100, 200 и 300 руб. соответственно. Песок доставляется на четыре строительных площадки, потребность которых составляет 40, 35, 30 и 45 т. Транспортные расходы на перевозку одной тонны песка заданы матрицей 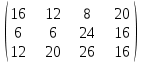 а) Определить оптимальный план закрепления строительных площадок за карьерами, если штраф за недопоставку песка на четвертую площадку составляет 100 руб. за тонну. б) Определить оптимальный план закрепления строительных площадок за карьерами при условии, что потребности четвертой строительной площадки должны быть удовлетворены полностью. в) Пусть недостающее количество песка можно обеспечить, увеличивая производительность либо первого, либо второго карьера. Определить оптимальный план закрепления строительных площадок за карьерами и оптимальный вариант расширения поставок песка. Задача 5. Три нефтеперегонных завода с ежедневной производительностью 6, 5 и 8 млн литров бензина снабжают три бензохранилища, ежедневная потребность которых составляет 4, 8 и 4 млн литров соответственно. Стоимость транспортировки составляет 10 руб. за 1000 литров на 1 км длины трубопровода. Расстояния в км – в табл. 11. Избыток продукции первый и второй заводы могут направить на другие хранилища на автоцистернах, расходы на транспортировку 1000 литров составят тогда 150 и 220 руб. соответственно. Третий завод может использовать излишки для собственных нужд. Найти оптимальную схему транспортировки. Таблица 11. Расстояние между пунктами транспортировки бензина, км.
Задача 6. Химическая компания владеет двумя заводами, которые производят химические компоненты для двух клиентов; потребности этих клиентов составляют 660 и 800 тонн продукции ежемесячно. Первый завод может производить от 400 до 800 тонн, а второй – от 450 до 900 тонн продукции ежемесячно. На первом заводе расходы на производство одной тонны продукции, без учета затрат на сырье, составляют 250, на втором – 280 руб. Сырье для заводов поставляют два поставщика, которые могут поставить не менее 500 тонн сырья по цене 200 руб. за тонну первому заводу и не менее 750 тонн по цене 210 руб. второму заводу. Химическая компания предполагает самостоятельно транспортировать и сырье, и готовую продукцию. Стоимость транспортировки одной тонны сырья от первого поставщика к заводам составляет 20 руб. для первого завода и 22 руб. – для второго. Аналогичные стоимости перевозок от второго поставщика равны 29 и 33 руб. соответственно. Стоимость перевозки одной тонны продукции от первого завода к клиентам 1 и 2 составляет 3 и 4, от второго завода – 5 и 2 руб. соответственно. Предположим, что из одной тонны сырья можно получить одну тонну готовой продукции. Сформулируйте и решите транспортную задачу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
