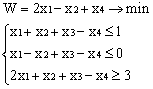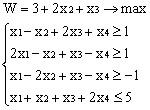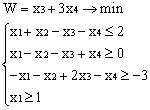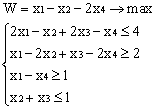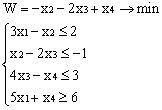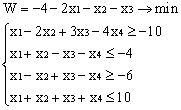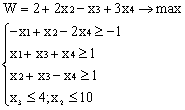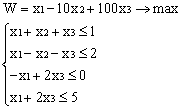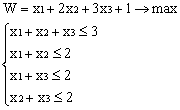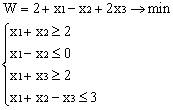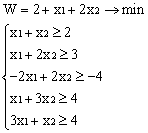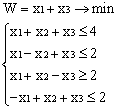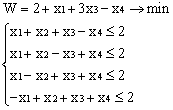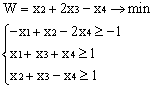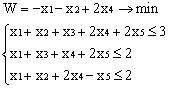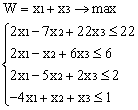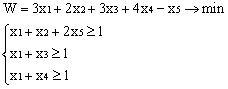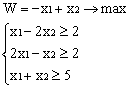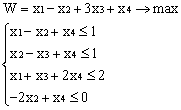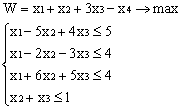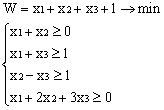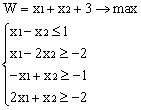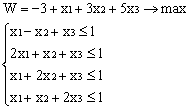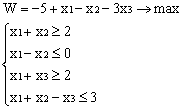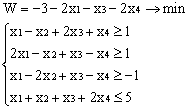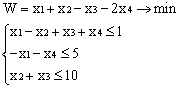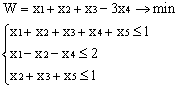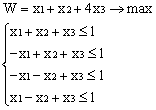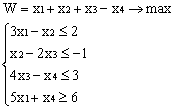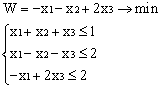Лабораторная работа 3 (2). Лабораторная работа Решение задачи лп симплекс методом в системе Excel
 Скачать 303.17 Kb. Скачать 303.17 Kb.
|
|
Лабораторная работа № 3. Решение задачи ЛП СИМПЛЕКС - МЕТОДОМ в системе Excel. Задание 1: разобрать пример реализации симплекс-метода. Сохранить файл в своей директории под именем ЛР_3. Каждое задание выполнять на отдельном листе. Этапы решения задачи. Привести задачу к каноническому виду введя дополнительные неотрицательные переменные x4, x5, x6 в каждое неравенство системы ограничений и в функцию цели с нулевыми коэффициентами. После приведения к каноническому виду система будет иметь следующий вид: Целевая функция : F = 9x1 + 10x2 + 16x3 + 0x4 + 0x5 + 0x6 max, система ограничений 18x1 + 15x2 + 12x3 +x4 360, 6x1 + 4x2 + 8x3 + x5 192, 5x1 + 3x2 + 3x3 + x6 180, xj 0, j = 1,6. 2. Создать на рабочем листе Excel таблицу исходных данных (Таблица 1) и присвоить имя SMT диапазону ячеек e6:k8.Создать матрицу базисных столбцов B= (x4, x5,x6 ) (Таблица 2) присвоить имя BAS диапазону ячеек a6:c8. Столбцы при переменных (x4, x5,x6 ) линейно независимы и образуют единичную матрицу. 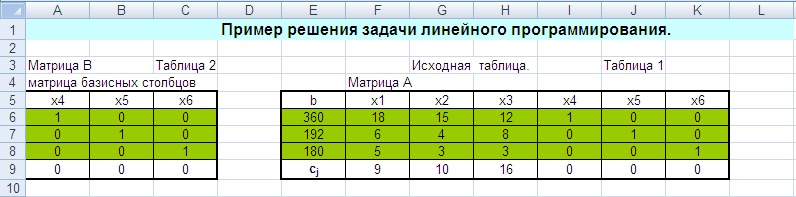 На следующем шаге необходимо создать расчетную симплекс таблицу в которой отразить алгоритм симплекс метода (Таблица 3). 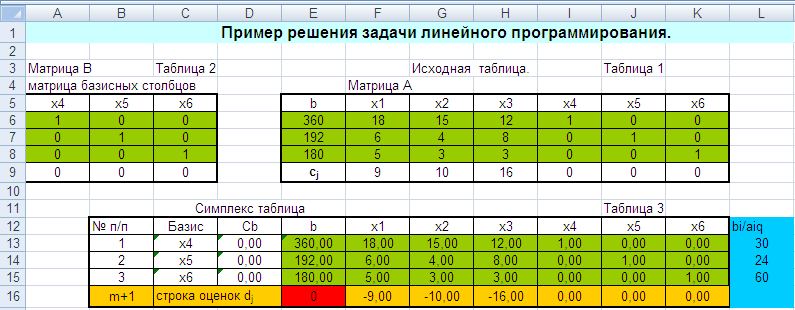 В столбце "Базис" введены формулы которые отражают имена базисных переменных соответствующих столбцам матрицы B. В столбце "Cb" соответствующие им коэффициенты целевой функции, взятые из последней строки матрицы B. Присвоить имя Cb диапазону ячеек D13:D15. Присвоить имя B диапазону ячеек E13:E15. В диапазон ячеек {e13:k15} вводится формула массива - {= МУМНОЖ(МОБР(BAS);SMT)}; /следует ввести формулу в ячейку Е13, затем выделить диапазон для копирования формулы {E13:K15} начиная с ячейки Е13, нажать F2 для отображения формулы и для копирования формулы нажать Ctrl+Shift+Enter/ строка m+1 содержит формулы для вычисления значения функции цели и для вычисления относительных оценок небазисных стобцов dj. К сожалению невозможно отразить формулы массива в данной таблице. В принципе после создания такой таблицы можно начинать процесс поиска оптимального решения, но лучше добавить еще одну таблицу, в которой определяется ведущий столбец и ведущая строка Таблица 4. 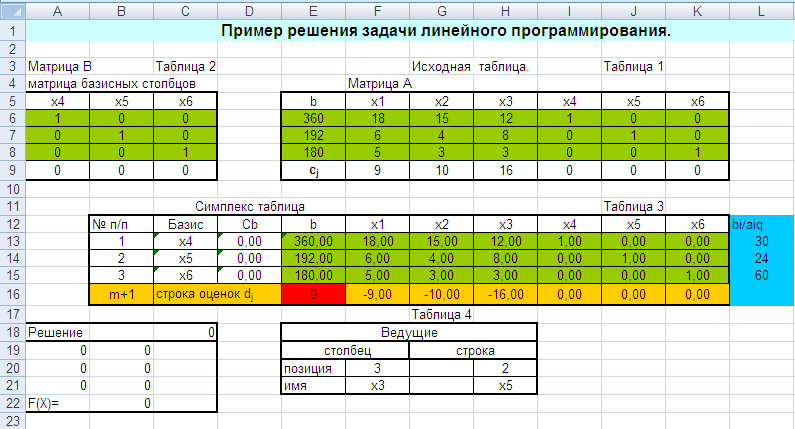 В таблице 4 используются две функции из категории "Ссылки и массивы": функция ПОИСКПОЗ(...) - для нахождения позиции ведущего столбца по минимальному значению относительной оценки небазисных столбцов; функция ИНДЕКС( . . . ) - для определения имени переменной вводимой в базис. В столбце L таблицы 3 введены формулы которые вычисляют отношение bi/ aiq для aiq >0 ведущего столбца. Образцы формул представлены ниже: 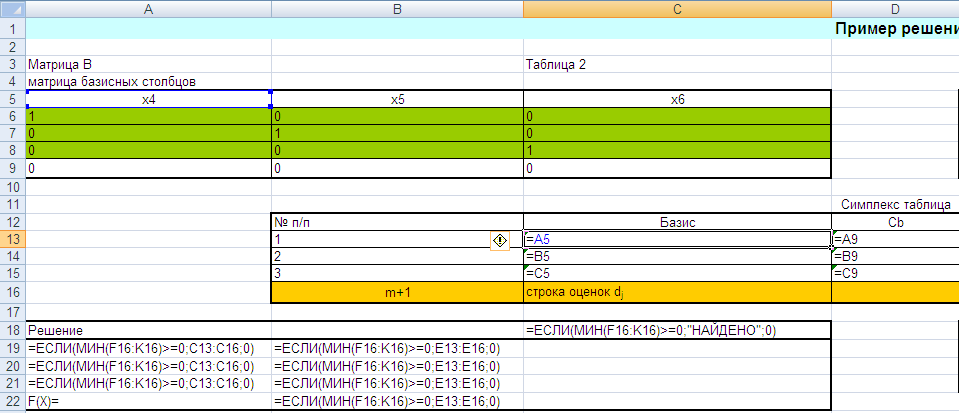 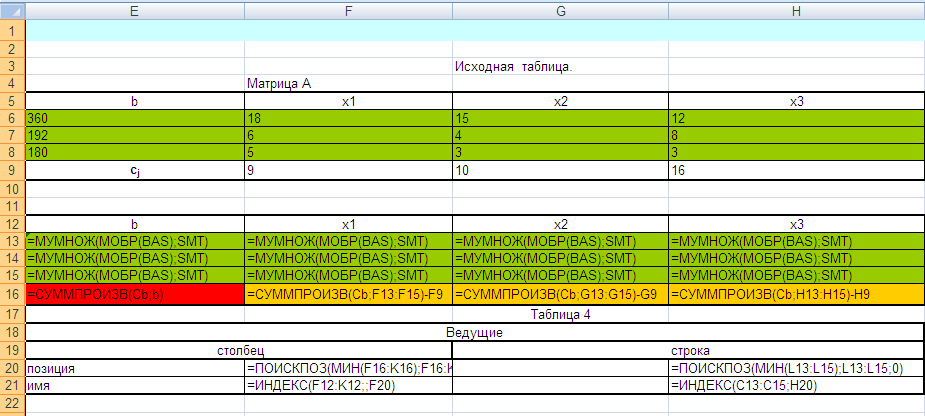 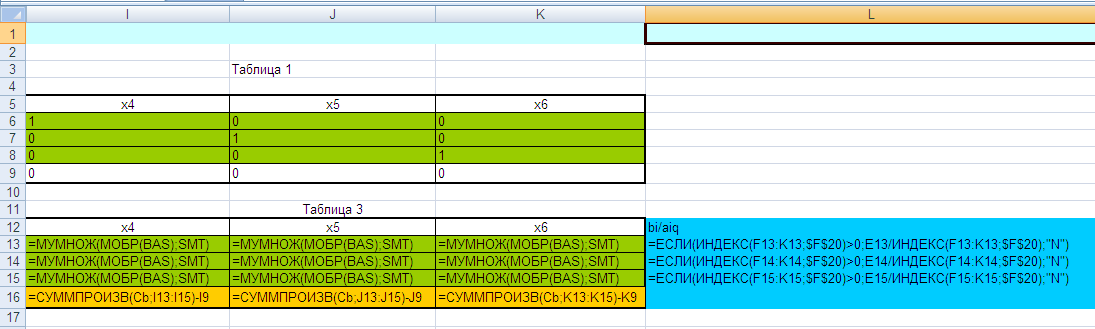 Из анализа данных в строке m+1 видно, что начальное решение не является оптимальным т.к. имеются отрицательные оценки небазисных столбцов. Таблица 4 говорит о том, что надо в базис ввести столбец соответствующий переменной x3 и вывести столбец для переменной x5. Для выполнения этой операции копируем из таблицы 1 столбец с именем x3 в таблицу 2 и вставляем его вместо столбца x5. В результате получим следующую таблицу: 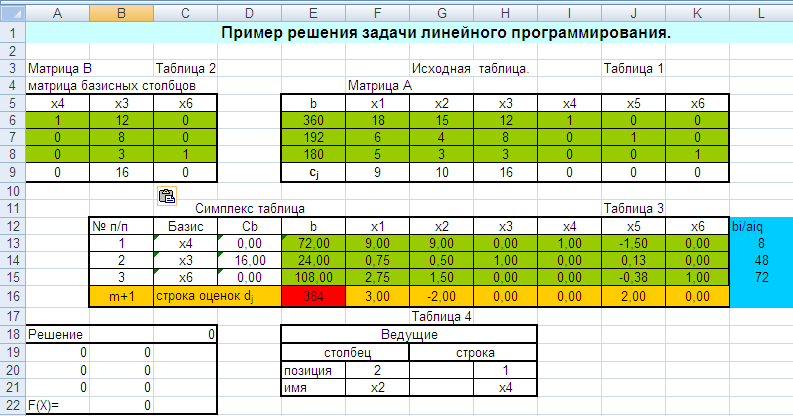 В результате получим новое решение но не оптимальное т.к. относительная оценка столбца x2 отрицательная. Из таблицы 4 следует, что нужно ввести в базис переменную x2, а вывести переменную x4. В скопировав столбец x2 таблицы 1 в таблицу 2 на место столбца x4 получим следующую таблицу. 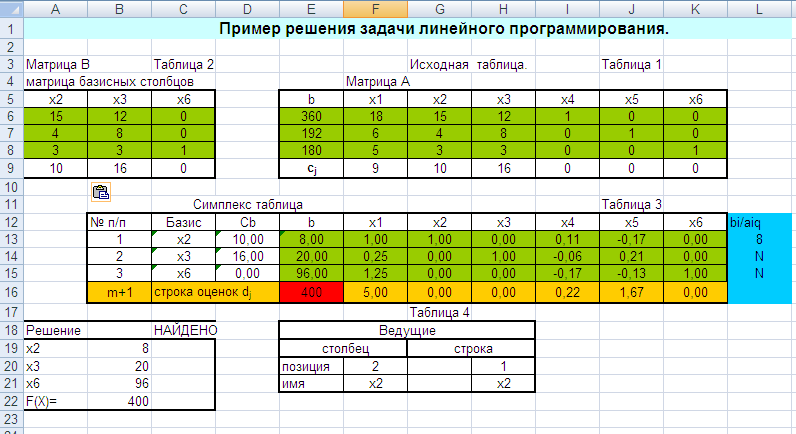 Таким образом оптимальное решение задачи будет следующее x1=0, x2=8,00, x3=20,00, x4=0, x5=0, x6=96,00, оптимальное значение целевой функции F(x)= 400. Задачи для самостоятельного решения. 1. Найти решение следующих задач линейного программирования 1. L=-x1+3x2 + 2x3 min при ограничениях x1 +x2 + 2x3 >= -5 2x1 - 3x2 + x3 <= 3 2x1 - 5x2 + 6x3 <= 5 xj>= 0, j = 1,3 2. Решить задачу линейного программирования симплекс-методом в среде Excel в соответствии со своим вариантом. Указание. Привести задачи к каноническому виду. Для каждой задачи построить на рабочем листе Excel симплекс таблицу. Найти оптимальное решение задачи. Определить число итераций необходимых для получения оптимального решения. Варианты заданий:
|