ТИДЗ_ИСТ014_Угарова_Шипунов_лр№7. Лабораторная работа 07 Решение задачи регрессии с помощью нейронной сети

Название	Лабораторная работа 07 Решение задачи регрессии с помощью нейронной сети
Дата	01.05.2023
Размер	0.55 Mb.
Формат файла
Имя файла	ТИДЗ_ИСТ014_Угарова_Шипунов_лр№7.docx
Тип	Лабораторная работа #1100508

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ

ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Кафедра информационных управляющих систем

Лабораторная работа № 07

«Решение задачи регрессии с помощью нейронной сети»

Вариант 3

Студенты гр. ИСТ-014________________________ Е.А Угарова, Д.В. Шипунов

(подпись)

Проверил ___________________________ В.Л. Литвинов

(оценка и подпись)

Цель:

Исследование принципов разработки нейронной сети на примере задачи регрессии

Задание на лабораторную работу:

1. Исследовать нейронную сеть при заданных начальных параметрах.

Найти минимальное значение n_hidden_neurons, при котором сеть дает

удовлетворительные результаты.

2. Найти наилучшее значение шага градиентного спуска lr в интервале ± 100% от номинального значения.

3. Изменить нейронную сеть для предсказания функции y = 2x * sin(2−x)

4. Для этой задачи (п. 3) получите метрику MAE =1𝑙∑ |𝑦_𝑝𝑟𝑒𝑑 𝑖 − 𝑦_𝑡𝑎𝑟𝑔𝑒𝑡 𝑖𝑙𝑖|

не хуже 0.03, варьируя: архитектуру сети, loss-функцию, lr оптимизатора или

количество эпох в обучении.
Теоретическая часть:

Регрессия – это односторонняя стохастическая зависимость, устанавливающая соответствие между случайными переменными, то есть математическое выражение, отражающее связь между зависимой переменной у и независимыми переменными х при условии, что это выражение будет иметь статистическую значимость.

Фактически, задача регрессии – это предсказание некоторого вещественного числа.

Методика исследования:

В начале нейронная сеть (рис 1.) насчитывает 40 нейронов в скрытом слое (n_hidden_neurons). При увеличении количества нейронов сеть будет решать всё более сложные задачи, но если их станет слишком много, то на решение задачи будет уходить больше времени. Скрытый слой является посредником между начальным и конечным значением. В нём хранятся некие промежуточные значения. Для решения используется ADAM, которая сочетает в себе идею накопления движения и идею более слабого обновления весов для типичных признаков с шагом (learning rate) 0.001.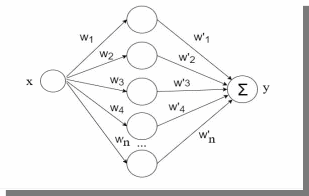

Рис. 1. Схема нейронной сети с одним скрытым слоем

Результаты исследования:

1. При заданных начальных значениях параметров результат после обучения выглядит неудовлетворительно (рис. 2).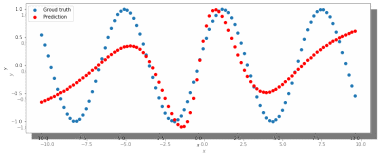

Рис. 2. ADAM, 40 нейронов, 2000 эпох, lr = 0.001

Увеличивая количество нейронов в скрытом слое до 100, наблюдаем небольшие изменения. (рис. 3).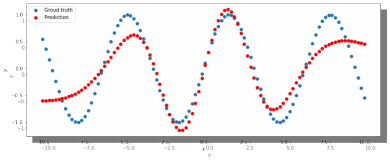

Рис. 3. ADAM, 100 нейронов, 2000 эпох, lr = 0.001

Было решено вернуться к 40 нейронам в скрытом слое, но увеличить количество эпох до 5000. Результат лучше, но всё ещё неудовлетворительный (рис. 4).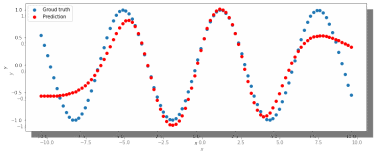

Рис. 4. ADAM, 40 нейронов, 5000 эпох, lr = 0.001

Только при увеличении нейронов в скрытом слое до 150 мы получаем удовлетворительный результат (рис. 5).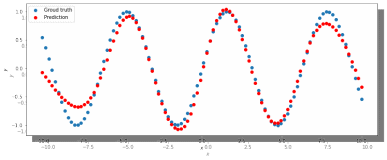

Рис. 5. ADAM, 150 нейронов, 5000 эпох, lr = 0.001

Таким образом, при минимальном значении, равном 150 нейронам в скрытом слое и при 5000 эпохах сеть даёт наиболее удовлетворительные результаты.

2. Попробуем изменить шаг градиентного спуска и проверить, какой будет результат работы нейросети (рис 6,7,8,9) с прежними параметрами: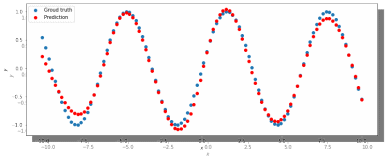

Рис. 6. ADAM, 150 нейронов, 5000 эпох, lr = 0.0001

Рис. 7. ADAM, 150 нейронов, 5000 эпох, lr = 0.0005

Рис. 8. ADAM, 150 нейронов, 5000 эпох, lr = 0.0015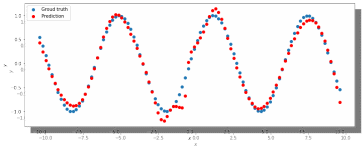

Рис. 9. ADAM, 150 нейронов, 5000 эпох, lr = 0.002

Проверим изначальное значение lr для нашей нейросети (рис. 10).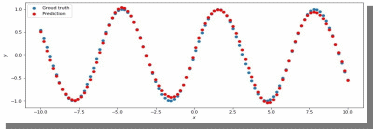

Рис.10. ADAM, 150 нейронов, 5000 эпох, lr = 0.001

Вывод:

Можно сказать, что лучшее значение lr = 0.001 для тех параметров, которые были использованы в 1 задании.

Если посмотреть на график потерь для lr = 0.0001 (рис. 11), можно понять, что нейросеть могла обучиться в дальнейших эпохах.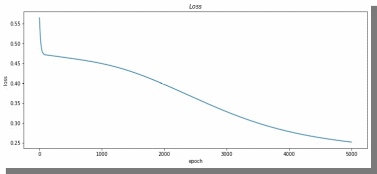

Рис. 11. График потерь для результата из рис. 6.

Для lr = 0.0001 увеличим количество эпох до 50000 и проверим результат (рис. 12):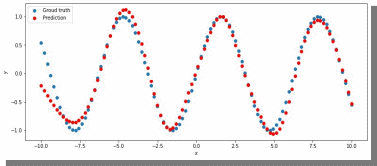

Рис. 12. ADAM, 150 нейронов, 50000 эпох, lr = 0.0001

График потерь выглядит следующим образом (рис. 13):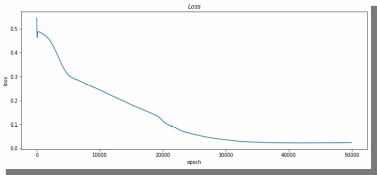

Рис. 13. График потерь для результата из рис. 12.

Аналогично если посмотреть на график потерь для lr = 0.002 (рис. 14), можно увидеть, что после 3000 эпохи нейросеть начала переобучаться и соответственно потери начали расти.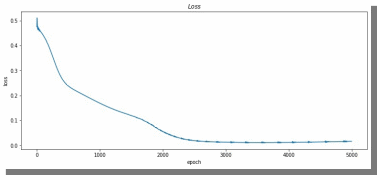

Рис. 14. График потерь для результата из рис. 9.

Уменьшим количество эпох до 3000 и посмотрим на результат (рис. 15):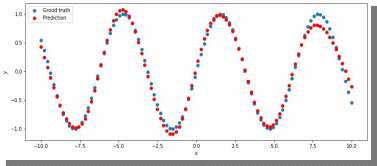

Рис. 15. ADAM, 150 нейронов, 3000 эпох, lr = 0.002

График потерь теперь выглядит следующим образом (рис. 16):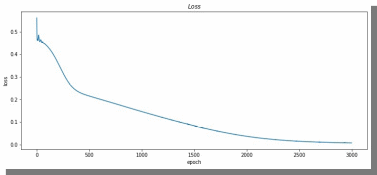

Рис. 16. График потерь для результата из рис. 15.

Таким образом, различные значения шага градиентного спуска зависят от других параметров и для оптимизации каждого из них, нужно подбирать подходящие значения остальных.

3. Изменим нашу нейросеть для предсказания функции y = 2^x*sin(2⁻^x) на следующую:

def target_function(x):

return 2**x * torch.sin(2**-x)

x_train = torch.linspace(-10, 5, 100)

y_train = target_function(x_train)

noise = torch.randn(y_train.shape) / 20.

y_train = y_train + noise

x_train.unsqueeze_(1)

y_train.unsqueeze_(1)

x_validation = torch.linspace(-10, 5, 100)

y_validation = target_function(x_validation)

x_validation.unsqueeze_(1)

y_validation.unsqueeze_(1)

Получившийся график: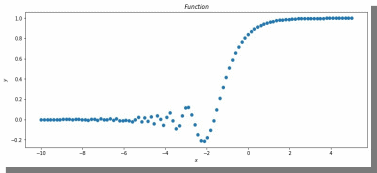

Рис. 17. график функции y = 2^x*sin(2⁻^x).

4. Получаем метрику MAE =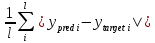

, добавляя данные:

def metric(pred, target):

return (pred - target).abs().mean()

print(metric(sine_net.forward(x_validation), y_validation).item())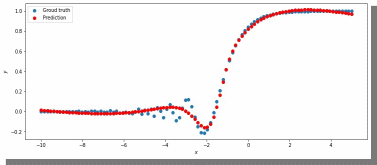

Рис.18. ADAM, 150 нейронов, 5000 эпох, lr = 0.001

Метрика: 0.022089794278144836

Лучшего результата удалось добиться, увеличив количество скрытых слоев и изменив параметры (рис.19).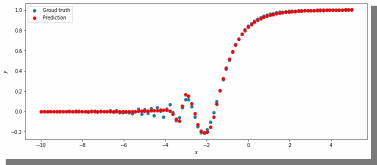

Рис.19. ADAM, 3 слоя: 100 нейронов, 150 нейронов, 50 нейронов,

5000 эпох, lr = 0.00125.

Метрика: 0.011302553117275238

В лучшем случае метрика получилась равной 0.011302553117275238, в остальных же попытках программа стабильно выдает 0,015-0,017.

Вывод:

Исследовали принципы разработки нейронной сети на примере задачи регрессии, изучили архитектуру простейшей нейронной сети и методы работы с обучением перцептрона, состоящего из 3 датасетов (тренировочного, валидационного и тестового). Провели работу с изменением гиперпараметров нейронной сети. Увеличив количество скрытых слоёв и подобрав значения остальных параметров, смогли добиться максимального функционала. Отчёт показывает, что путём изменения данных и анализом ошибок с последующим устранением, оптимизацией программы, цель лабораторной работы была достигнута.