РЦИС - ЛР11 БРР. Лабораторная работа 1 1 Временная дискретизация и восстановление непрерывных сигналов. Выполнил студент группы брр1601
 Скачать 276.96 Kb. Скачать 276.96 Kb.
|
|
Федеральное агентство связи Государственное образовательное учреждение высшего профессионального образования Московский Технический Университет Связи и Информатики (МТУСИ) Кафедра общей теории связи Лабораторная работа №11 Временная дискретизация и восстановление непрерывных сигналов. Выполнил студент группы БРР1601 Савенко С.С. Цель работы. Теоретическое и экспериментальное изучение временной дискретизации непрерывных сигналов, способы восстановления исходной функции по её отсчётам, факторов, влияющих на точность восстановления. Домашнее задание. Вариант 3. Исходные данные: 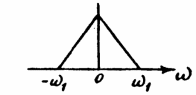 Период следования отсчётных импульсов, Δt: 2 мс; Длительность, τ: 0.3Δt; Частота среза, ωв идеального ФНЧ: 2π103 рад/с; Спектр исходной непрерывной функции Sx(ω), где ω1= 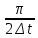 ; ; Sx(ω) R1= 3*103 Ом; С1= 0.33*10-6 Ф; 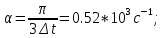 Временная диаграмма одиночного δ-импульса имеет вид: 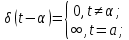 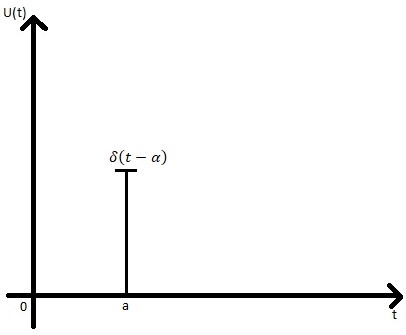 Спектр одиночного δ-импульса получили, используя преобразование Фурье: 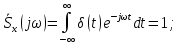 Использовано фильтрующее свойство δ-функций: 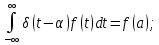 Следовательно, спектр одиночного δ-импульса имеет вид: 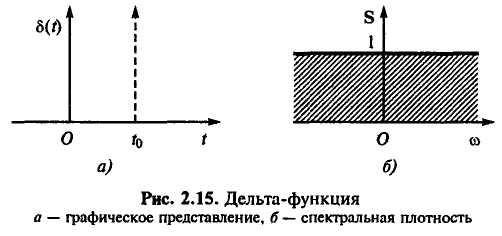 Временная диаграмма периодической последовательности δ-импульсов с периодом T= 2Δt= 2 мс имеет вид: 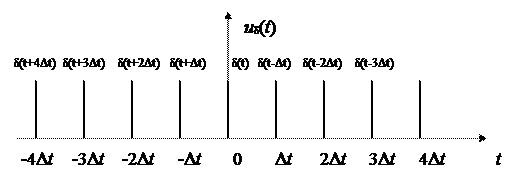 Так как сигнал периодический, то его спектр будет дискретным: 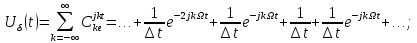 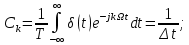 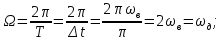 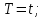 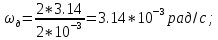 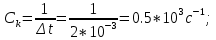 Спектр периодической последовательности δ-импульсов в соответствии с формулой для Uδ(t) имеет вид: 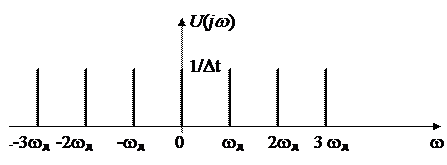 Спектр дискредитированного сигнала имеет следующий вид: 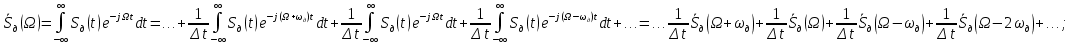 Таким образом мы видим, что спектр дискретизированного сигнала содержит спектр исходного сигнала Sx(ω), спектр исходного сигнала, смещённый на величину частоты дискретизации вправо Sx(ω- 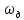 ), тот же спектр, смещённый на величину частоты дискретизации влево Sx(ω+ ), тот же спектр, смещённый на величину частоты дискретизации влево Sx(ω+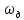 ), тот же спектр, смещённый на величину 2 ), тот же спектр, смещённый на величину 2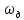 и так далее. и так далее.Спектр исходного непрерывного сигнала: 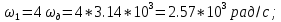 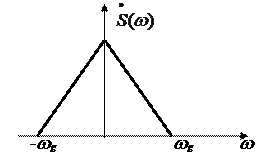 Спектр дискретизированного сигнала: 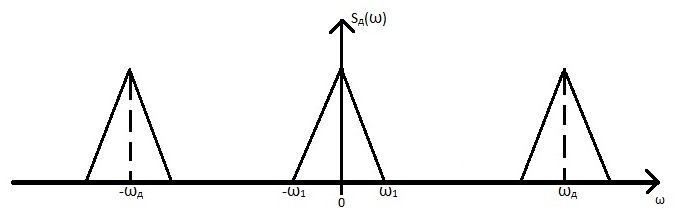 Спектр дискретизированного сигнала при дискретизации импульсами конечной длительности (АИМ): Спектр дискретизированного сигнала импульсами конечной длительности, следовательно, похож на спектр дискретизированного сигнала при дискретизации дельта-импульсами, но амплитуда составляющих спектра убывает с ростом номера гармоники: 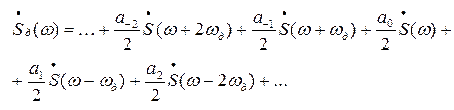 Коэффициенты ак – это коэффициенты разложения в ряд Фурье периодической последовательности прямоугольных импульсов. 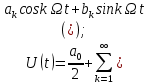 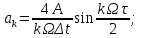 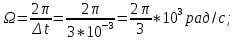 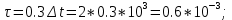 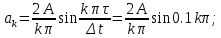 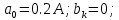 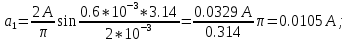 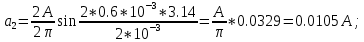 Спектр АИМ сигнала условно: АЧХ идеального ФНЧ имеет вид: 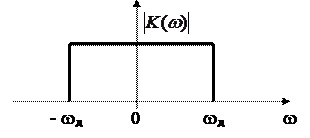 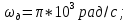 Импульсная реакция ИФНЧ, т. Е. реакция на δ-импульс имеет вид: Δt 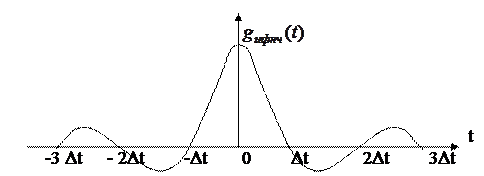 =2 мс; =2 мс;  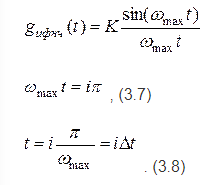 АЧХ RC ФНЧ имеет вид: 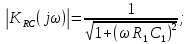 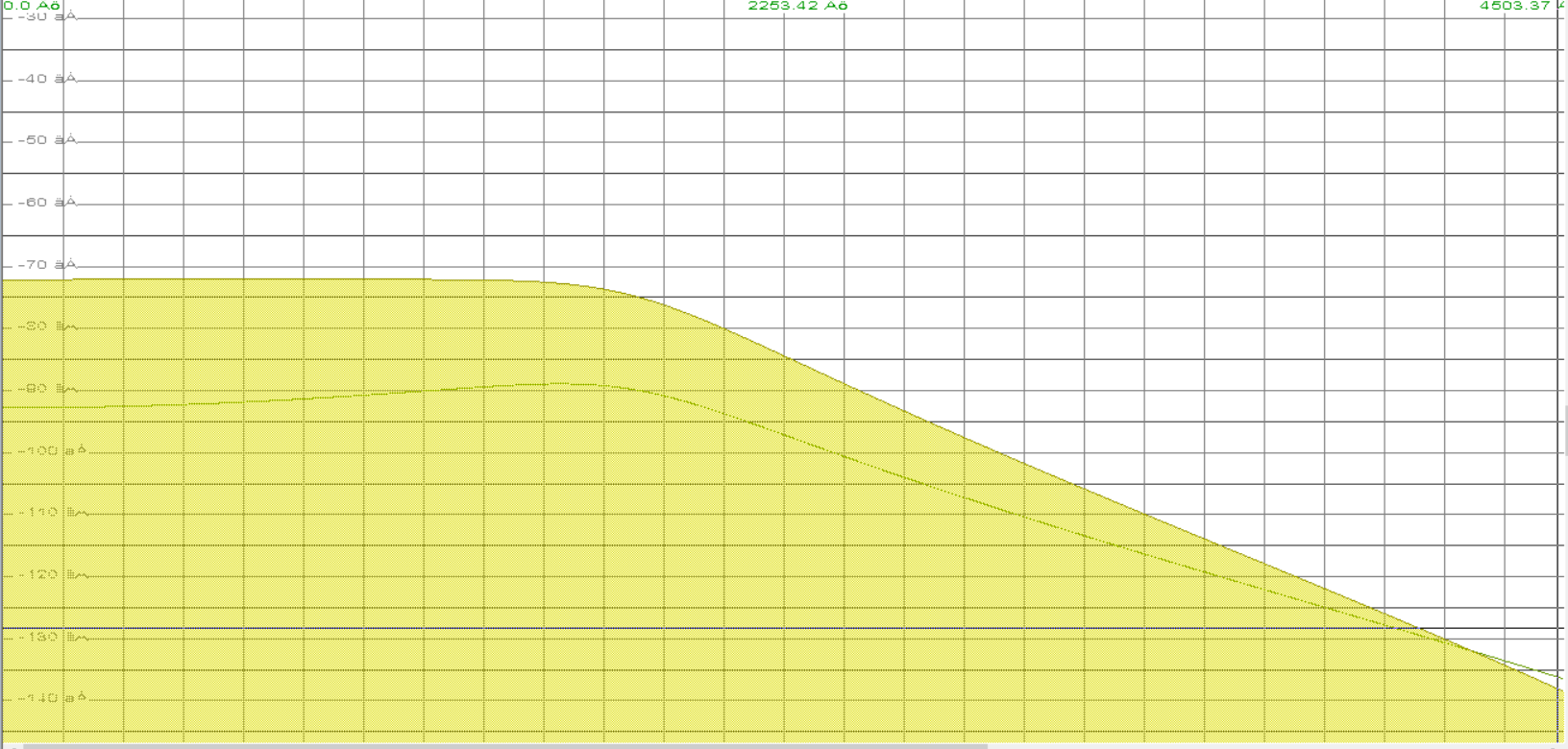 Импульсная реакция фильтра равна: 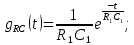 Выполнение. Тест 1. 1) Функция полностью. Определяется своими отсчётами, взятыми в моменты времени к T, T= 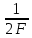 , если спектр этой функции не содержит частот выше F; , если спектр этой функции не содержит частот выше F;2) Введите номер диаграммы непрерывного сигнала: 3) Введите номер диаграммы дискретизированного сигнала: 4) Сигнал АИМ: 5) Интервал дискретизации Т: T= 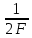 ; ;6) Интервал дискретизации Т: T= 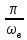 ; ;7) Ряд Котельникова: 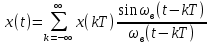 ; ;Тест 2. 1) Амплитудный спектр – зависимость комплексных амплитуд составляющих сигнала от частоты; 2) Одиночный дельта импульс: 3) Периодическая последовательность дельта импульсов: 4) Периодическая последовательность импульсов: 5) Спектральная диаграмма одиночных дельта импульсов: 6) Диаграмма последовательности дельта импульсов: 7) Спектральная диаграмма последовательных импульсов: 8) Формула спектра АМ сигнала: 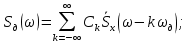 Тест 3. 1) Для восстановления исходного непрерывного сигнала импульсы следует подать на вход идеального ФНЧ; 2) АЧХ ИФНЧ: 3) АЧХ RC ФНЧ: 4) Импульсная реакция ИФНЧ: 5) Импульсная реакция RC ФНЧ: 6) СКП дискретизации аналогового сигнала: 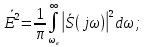 Москва 2018 |
