лабораторная работа. Работа-3. Лабораторная работа 3 Исследование дискретизации непрерывных сигналов Методические указания и задания
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
 Федеральное агентство связи Ордена Трудового Красного Знамени федерального государственного бюджетного образовательного учреждения высшего образования «Московский технический университет связи и информатики» Волго-Вятский филиал Кафедра инфокоммуникационных и общепрофессиональных дисциплин (ИКиОПД) Общая теория связи Лабораторная работа № 3 «Исследование дискретизации непрерывных сигналов» Методические указания и задания Выполнил: Проверил: Чернявский А.Д. Нижний Новгород 2021 Цель работы. Изучение основ дискретизации и восстановления непрерывных сигналов по теореме В. А. Котельникова. 2.Теоретическая часть. В настоящее время все радиоэлектронные системы, включая системы телефонии, радиовещания и телевидения, переходят на цифровой режим работы. В основе преобразования различных непрерывных (аналоговых) сигналов для их обработки в цифровой форме лежит процедура дискретизации. В связи с этим вводятся следующие понятия: непрерывный (аналоговый) сигнал – это сигнал x(t), который является непрерывным как во времени, так и по значению; дискретный сигнал  , где k = 0, ±1, ±2, ±3, … – это сигнал, который получается в результате дискретизации значений аналогового сигнала x(t); , где k = 0, ±1, ±2, ±3, … – это сигнал, который получается в результате дискретизации значений аналогового сигнала x(t);дискретизация – это определение значений аналогового сигнала в дискретные моменты времени. Пример аналогового сигнала, подвергшегося дискретизации, показан на рисунке 2.1. Отметим, что после дискретизации, представленной на рисунке 2.1, аналоговый сигнал представлен только в дискретные моменты времени.  Рисунок 2.1 – Пример аналогового сигнала, подвергшегося дискретизации Как правило, при дискретизации отсчеты аналогового сигнала берутся через равные промежутки времени  (рисунок 2.1), называемые периодом дискретизации (или интервалом, шагом дискретизации – sample time). (рисунок 2.1), называемые периодом дискретизации (или интервалом, шагом дискретизации – sample time).Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency):  . .Таким образом, дискретный сигнал непрерывен по амплитуде, но определяется только в дискретных точках во времени. Ясно, что в общем случае представление аналогового сигнала набором дискретных отсчетов приводит к потере информации, так как остается неизвестным поведении сигнала в промежутках между отсчетами (выборками). Однако существует класс аналоговых сигналов, для которых такой потери информации не происходит и которые могут быть точно восстановлены по значениям своих дискретных отсчетов. К этому классу относятся сигналы, подчиняющиеся теореме, сформулированной в 1933 году выдающимся отечественным ученым Владимиром Александровичем Котельниковым: «Любой сигнал s(t), спектр которого не содержит составляющих с частотами выше некоторой верхней граничной частоты fB, может быть без потерь информации представлен своими дискретными отсчетами, взятыми с интервалом 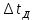 , удовлетворяющим следующему неравенству: , удовлетворяющим следующему неравенству: Примечание – В зарубежных источниках данная теорема называется теоремой Найквиста (Nyquist theorem), а также теоремой Шеннона (Shannon theorem) или теоремой дискретизации (sampling theorem). Таким образом, если fB – самый высокочастотный компонент сигнала, то, чтобы элементы выборки полностью описывали сигнал, дискретизация сигнала должна осуществляться с частотой не ниже 2fB т. е. Очевидно, увеличение частоты дискретизации сигнала приводит к росту скорости создания сообщений, что вызывает увеличение необходимой пропускной способности канала связи. Поэтому актуальна задача выбора частоты дискретизации (периода дискретизации), обеспечивающей минимум скорости создания сообщений при заданной погрешности восстановления исходного непрерывного сигнала x(t) по набору его дискретных отсчетов. Восстановление исходного непрерывного сигнала x(t) по набору его дискретных отсчетов {x(k 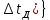 производится по формуле: производится по формуле: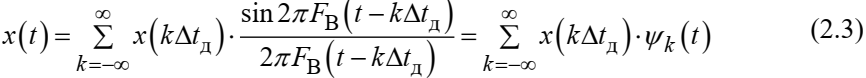 Формула (2.3) представляет собой разложение сигнала s(t) в ряд по системе функций { 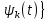 называемой базисом Котельникова: называемой базисом Котельникова: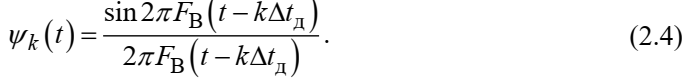 Формирование непрерывного сигнала по его дискретным отсчетам поясняет рисунок 2.2. Пунктиром показаны графики отдельных слагаемых формулы (2.3), сплошной линией – восстановленный аналоговый сигнал. 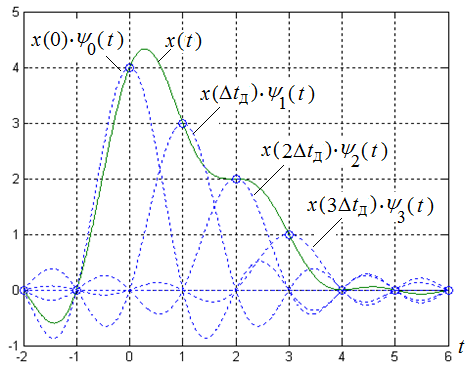 Рисунок 2.2 – Восстановление аналогового сигнала по его дискретным отсчетам Рисунок 2.2 наглядно демонстрирует главное свойство сигнала с ограниченным спектром – его бесконечность во времени. Хотя отличны от нуля лишь несколько отсчетов показанного сигнала, аналоговый сигнал оказывается бесконечно колеблющимся между нулевыми отсчетами (на рисунке это отсчеты с номерами –2, –1, 4, 5, 6) его значения отличны от нуля. Эти колебания нигде не заканчиваются, хотя их амплитуда стремится к нулю. Таким образом, для полного восстановления непрерывного сигнала x(t) по набору его дискретных отсчетов { 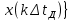 необходимо просуммировать бесконечное множество членов ряда (2.3). Однако если функция с ограниченным спектром x(t) рассматривается на конечном интервале времени T (рисунок 2.3), то точное разложение (2.3) можно заменить следующим приближённым разложением: необходимо просуммировать бесконечное множество членов ряда (2.3). Однако если функция с ограниченным спектром x(t) рассматривается на конечном интервале времени T (рисунок 2.3), то точное разложение (2.3) можно заменить следующим приближённым разложением: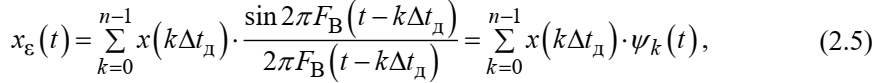 где n – конечное число дискретных отсчетов, ед., непрерывного сигнала x(t), определяющее восстановленный сигнал при 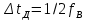 . .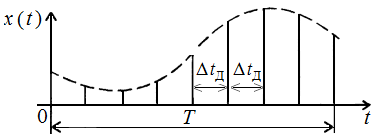 Рисунок 2.3 – Функция с ограниченным спектром x(t) рассматривается на конечном интервале времени T Конечное число дискретных отсчетов n, ед., укладывающихся на конечном интервале времени T, рассчитывается по формуле  Параметр 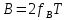 в формуле (2.6) называют базой сигнала. Очевидно, что погрешность восстановления сигнала при ограничении числа его отсчётов n будет тем больше, чем меньшее число слагаемых учитывается при суммировании в формуле (2.5). в формуле (2.6) называют базой сигнала. Очевидно, что погрешность восстановления сигнала при ограничении числа его отсчётов n будет тем больше, чем меньшее число слагаемых учитывается при суммировании в формуле (2.5).Оценим качественно погрешность 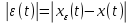 . Поскольку все слагаемые ряда (2.5) обращаются при t=i∆ . Поскольку все слагаемые ряда (2.5) обращаются при t=i∆ в нуль во всех точках, за исключением, слагаемого с номером k = i, то в этих сечениях значения совпадают с x(t), т. е. погрешность в нуль во всех точках, за исключением, слагаемого с номером k = i, то в этих сечениях значения совпадают с x(t), т. е. погрешность  равна нулю; очевидно, погрешность достигнет наибольшей величины внутри промежутка между отсчётами. Кроме того, величина погрешности нарастает к краям рассматриваемого интервала времени T (рисунок 2.4). Таким образом, приходим к выводу, что первой причиной погрешности восстановления функции с ограниченным спектром x(t по совокупности её дискретных отсчетов) определенных на конечном интервале времени T (формула (2.5)) является то, что число таких дискретных отсчетов конечно. равна нулю; очевидно, погрешность достигнет наибольшей величины внутри промежутка между отсчётами. Кроме того, величина погрешности нарастает к краям рассматриваемого интервала времени T (рисунок 2.4). Таким образом, приходим к выводу, что первой причиной погрешности восстановления функции с ограниченным спектром x(t по совокупности её дискретных отсчетов) определенных на конечном интервале времени T (формула (2.5)) является то, что число таких дискретных отсчетов конечно. Рисунок 2.4 – Изменение погрешности  в пределах интервала времени T в пределах интервала времени TДругая причина погрешностей обусловлена тем, что спектры реальных непрерывных (аналоговых) сигналов не обращаются в нуль за пределами верхней граничной частоты аналогового сигнала fB, Гц. Хотя основная энергия сигналов расположена на частотах от –fB до fB, некоторая часть энергии приходится на частоты выше граничной. С учетом этого, относительная среднеквадратическая погрешность восстановления исходного непрерывного сигнала x(t) по набору его дискретных отсчетов {  определяется соотношением определяется соотношением где ∆E – та часть энергии, которая оказывается за пределами полосы частот от –fB до fB и не учитывается при восстановлении сигнала, В2с; Е – полная энергия сигнала x(t),  ; ; – квадрат нормы сигнала x(t), – квадрат нормы сигнала x(t),  . .Таким образом, при заданной погрешности (2.7) можно определить необходимую граничную частоту fB, а, следовательно, и интервалы между отсчётами (период дискретизации). Детальное исследование показывает, что погрешности за счёт неучитываемой части спектра сигнала будут тем больше, чем медленнее убывает спектр сигнала за пределами граничной частоты fB. Третьей причиной погрешностей восстановления функции с ограниченным спектром x(t по совокупности её дискретных отсчетов) определенных на конечном интервале времени T являются неидеальные характеристики фильтра нижних частот (ФНЧ), формирующего функции {  , образующие базис Котельникова на приемной стороне канала связи. , образующие базис Котельникова на приемной стороне канала связи.Как известно из лекционного курса, колебания, имеющие форму базисной функции Котельникова вида (2.4), можно получить на выходе идеального ФНЧ с граничной частотой fB при действии на его входе дельта-импульса δ(t). Амплитудно-частотная характеристика (АЧХ) идеального ФНЧ равномерна (рисунок 2.5)  где  – комплексная передаточная функция идеального ФНЧ. – комплексная передаточная функция идеального ФНЧ. Рисунок 2.5 – Идеальные и реальные частотные характеристики ФНЧ, формирующего функции { 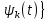 , образующие базис Котельникова на приемной стороне канала связи , образующие базис Котельникова на приемной стороне канала связиВ свою очередь, фазочастотная характеристика (ФЧХ) – линейна (рисунок 2.5): 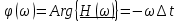 где ∆t=1/2fB – постоянная времени (задержки) идеального ФНЧ. Как известно из курса теории электрических и радиотехнических цепей, импульсная характеристика фильтра hδ(t) может быть определена на основе обратного интегрального преобразования Фурье от комплексной передаточной функции 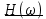 фильтра: фильтра: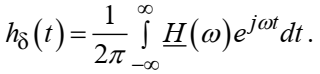 Для рассматриваемого случая идеального ФНЧ импульсная характеристика фильтра hδ(t) определяется соотношением вида 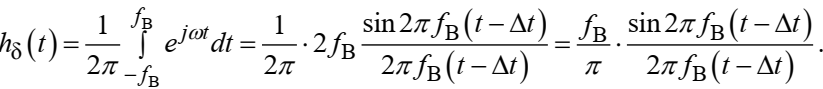 Характеристики реальных фильтров 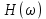 и и 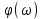 пунктирные кривые на рисунке 2.5), используемых на приемной стороне канала связи, отличаются от идеальных (сплошные кривые на рисунке 2.5). Это приводит к отклонениям реальных функций { пунктирные кривые на рисунке 2.5), используемых на приемной стороне канала связи, отличаются от идеальных (сплошные кривые на рисунке 2.5). Это приводит к отклонениям реальных функций {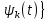 (пунктирная кривая на рисунке 2.6), образующих базис Котельникова на приемной стороне канала связи, от идеальных (сплошная кривая на рисунке 2.6) и, как следствие, к появлению дополнительных погрешностей восстановления сигнала x(t) по набору его дискретных отсчетов { (пунктирная кривая на рисунке 2.6), образующих базис Котельникова на приемной стороне канала связи, от идеальных (сплошная кривая на рисунке 2.6) и, как следствие, к появлению дополнительных погрешностей восстановления сигнала x(t) по набору его дискретных отсчетов { , k = 0, 1, 2, … , n – 1, определенных на конечном интервале времени T. , k = 0, 1, 2, … , n – 1, определенных на конечном интервале времени T. Рисунок 2.6 – Идеальные и реальные базисные функции Котельникова. Таким образом, для применения теоремы В. А. Котельникова на практике необходимо определить верхнюю граничную частота аналогового сигнала fB, Гц. Методика определения верхней граничной частоты сигнала fB с использованием двух подходов (информационного и энергетического) была рассмотрена на первом лабораторном занятии «Исследования числовых параметров сигналов». Воспользуемся результатами примера, рассмотренного на первом лабораторном занятии, связанными с анализом числовых параметров сигнала представляющего собой прямоугольный импульс высотой A и длительностью τ и рассмотрим методику его дискретизации и восстановления по теореме В.А. Котельникова. Оборудование и материалы Аппаратура. Для выполнения лабораторной работы необходим персональный компьютер. Программное обеспечение. Для выполнения лабораторной работы необходима операционная система WINDOWS, программа MathCAD 13 и выше. Указания по технике безопасности При выполнении лабораторной работы запрещается: самостоятельно производить ремонт персонального компьютера, а также установку и удаление имеющегося программного обеспечения; нарушать общепринятые правила техники безопасности при работе с электрооборудованием, в частности, касаться электрических розеток металлическими предметами и т.д.; принимать пищу, напитки и сорить на рабочем месте пользователя персонального компьютера. В случае неисправности персонального компьютера необходимо немедленно сообщить об этом обслуживающему персоналу лаборатории (системному администратору, оператору). Указания по порядку выполнения работы Методику выполнения работы рассмотрим на следующем примере. Задан непрерывный сигнал s(t), представляющий собой прямоугольный импульс высотой A = 1 В и длительностью τ = 1 мс =  с. Аналитическое описание сигнала представлено формулой с. Аналитическое описание сигнала представлено формулой Требуется определить: верхнюю граничную частоту спектра fВ, Гц, и базу сигнала s(t), используя энергетический подход; период ∆tд , с, и частоту fД , Гц, дискретизации непрерывного сигнала s(t), удовлетворяющие теореме В. А. Котельникова; n – количество отсчетов дискретного сигнала (k = 0, 1, 2, … , n – 1); дискретный сигнал s(k∆  ), полученный в результате дискретизации непрерывного сигнала s(t); ), полученный в результате дискретизации непрерывного сигнала s(t);функции {  , составляющие базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его дискретных отсчетов s(k∆ , составляющие базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его дискретных отсчетов s(k∆ ), (построить графики для нескольких первых базисных функций, например, для k = 0, 1, 2, ...); ), (построить графики для нескольких первых базисных функций, например, для k = 0, 1, 2, ...);несколько первых слагаемых, стоящих под знаком суммы в правой части формулы (2.3) и представляющих собой произведение k-го дискретного отсчета s(k∆  ), на k-ю базисную функцию ), на k-ю базисную функцию  (построить графики, например, для k = 0, 1, 2, ...) и результат их суммирования; (построить графики, например, для k = 0, 1, 2, ...) и результат их суммирования;функцию  , представляющую результат восстановления исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ , представляющую результат восстановления исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ )} (построить график) и построить в той же координатной сетке график исходного непрерывного сигнала s(t); )} (построить график) и построить в той же координатной сетке график исходного непрерывного сигнала s(t);функцию  , представляющую модуль разности между сигналами , представляющую модуль разности между сигналами  и s(t) (построить график); и s(t) (построить график); квадрат расстояния между сигналами  и s(t); и s(t);квадрат расстояния между сигналами  и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t); и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t);Кроме того, необходимо исследовать, как влияет изменение верхней граничной частоты спектра fВ, Гц, сигнала s(t) на квадрат расстояния между сигналами  и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t). и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t).Рассмотрим решение поставленной задачи в математическом пакете Mathcad: Запускаем математический пакет Mathcad. Согласно (2.8) и заданным параметрам вводим математическое определение непрерывного сигнала s(t ) и строим его график (рисунок 2.7).  Рисунок 2.7 – Определение и график непрерывного сигнала s(t) 2. По рассмотренной в лабораторной работе методике определяем верхнюю граничную частоту спектра fВ сигнала s(t) на основе энергетического подхода, полагая коэффициент уменьшения энергии сигнала по причине искусственного ограничения ширины его спектра KE равным 0,903: 2.1 Находим по формуле (1.30) спектральную функцию сигнала s(t) (рисунок 2.8);  Рисунок 2.8 – Определение спектральной функции сигнала s(t) 2.2 Используя результаты определения верхней эффективной граничной частоты спектра сигнала, полученные на первой лабораторной работе, выполним следующие действия: зададимся начальным приближением параметра fB = 1 кГц (fb:= 1); запишем в блоке Given уравнение относительно искомой граничной частоты спектра fb, полагая коэффициент уменьшения энергии сигнала по причине искусственного ограничения ширины его спектра диапазоном от –fb до fb, равным 0,903 (рисунок 2.9)  Рисунок 2.9 – Определение граничной частоты спектра сигнала s(t) Приходим к выводу, что первый лепесток спектральной функции содержит 90,3% энергии прямоугольного импульса (рисунок 2.10).  Рисунок 2.10 – Граничные частоты спектра прямоугольного импульса53 Примечания: Системы линейных и нелинейных уравнений и неравенств позволяет решать на Mathcad блок Given в сочетании с функцией Find. Внимание! В блоке Given записывается система уравнений и/или неравенств, подлежащих решению. Система уравнений и/или неравенств должна быть записана после или правее слова Given. При записи уравнений вместо знака = следует набирать Ctrl+= Перед словом Given необходимо указывать начальные приближения для всех переменных. Блок Given не пригоден для поиска индексированных переменных. Признаком окончания системы уравнений служит функция Find, если вы хотите найти точное решение системы, либо функция Minerr, если система не может быть решена точно, и есть желание найти наилучшее приближение, обеспечивающее минимальную погрешность. Функции Minerr и Find должны иметь столько же или меньше аргументов, сколько уравнений и неравенств содержит блок Given. Если окажется, что блок содержит слишком мало уравнений или неравенств, то его можно дополнить тождествами или повторяющимися выражениями. В том случае, если решение не может быть найдено при заданном выборе начального приближения, появится сообщение в красной рамке Did not find solution – решение не найдено. 3.В соответствии с теоремой Котельникова, вычисляем по формуле (2.2) частоту дискретизации fД , кГц, и период дискретизации ∆tд , мс, сигнала s(t) (рисунок 2.11). Рисунок 2.11 – Вычисление частоты дискретизации и периода дискретизации сигнала s(t) Как видно из расчетов, приведенных на рисунке 2.11, частота дискретизации fД сигнала s(t), удовлетворяющая теореме Котельникова, составляет 2 кГц, а период дискретизации ∆tд соответственно равен 0,5 мс. 4. По формуле (2.6) определяем количество отсчетов дискретного сигнала (рисунок 2.12). Рисунок 2.12 – Определение количества отсчетов дискретного сигнала Примечание – Встроенная в Mathcad функция floor(z) возвращает целое число меньшее или равное z. Например, floor (3.364) = 2. 5. Формируем вектор дискретных отсчетов {s(k∆  )} (k = 0, 1, 2) непрерывного сигнала s(t) и строим временную диаграмму дискретного сигнала (рисунок 2.13). )} (k = 0, 1, 2) непрерывного сигнала s(t) и строим временную диаграмму дискретного сигнала (рисунок 2.13). Рисунок 2.13 – Вектор дискретных отсчетов и временная диаграмма дискретного сигнала 6. По формуле (2.4) определяем функции {  , составляющие базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ , составляющие базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ )} (рисунок 2.14). )} (рисунок 2.14).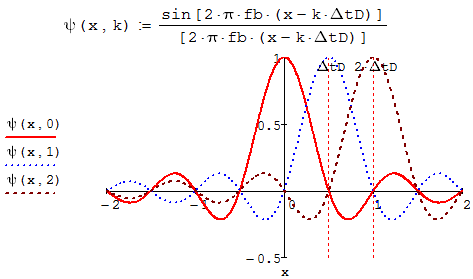 Рисунок 2.14 – Определение функций { 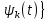 , составляющих базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ , составляющих базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ )} )}7. Определяем три слагаемых, стоящих под знаком суммы в правой части формулы (2.5): произведение k-го дискретного отсчета s(k∆  ) на k-ю базисную функцию ) на k-ю базисную функцию 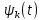 , (k = 0, 1, 2) и результат их суммирования (рисунок 2.15). , (k = 0, 1, 2) и результат их суммирования (рисунок 2.15).  Рисунок 2.15 – Определение несколько первых слагаемых, стоящих под знаком суммы в правой части формулы (2.5) и результата их суммирования 8. По формуле (2.5) определяем функцию  , представляющую результат восстановления исходного непрерывного сигнала s(t) по трем его дискретным отсчетам {s(k∆ , представляющую результат восстановления исходного непрерывного сигнала s(t) по трем его дискретным отсчетам {s(k∆ )} , строим его график и график исходного непрерывного сигнала s(t) (рисунок 2.16). )} , строим его график и график исходного непрерывного сигнала s(t) (рисунок 2.16). Рисунок 2.16 – Графики функции  , представляющей результат восстановления исходного непрерывного сигнала s(t) по трем его дискретным отсчетам {s(k∆ , представляющей результат восстановления исходного непрерывного сигнала s(t) по трем его дискретным отсчетам {s(k∆ )} , и исходного непрерывного сигнала s(t) )} , и исходного непрерывного сигнала s(t)6. Строим график функции  , т. е. погрешности восстановления исходного непрерывного сигнала s(t) по трем его дискретным отсчетам {s(k∆ , т. е. погрешности восстановления исходного непрерывного сигнала s(t) по трем его дискретным отсчетам {s(k∆ )} (рисунок 2.17). )} (рисунок 2.17). Рисунок 2.17 – График функции 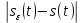 7. По формулам (2.7) и (2.8) определяем расстояние и квадрат расстояния между сигналами  и s(t) (рисунок 2.18). и s(t) (рисунок 2.18).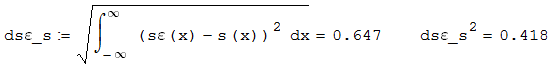 Рисунок 2.18 – Определение расстояния и квадрата расстояния между сигналами  и s(t) и s(t) 8. По формулам (2.4) и (2.6) определяем норму и квадрат нормы сигнала s(t) (рисунок 2.19). 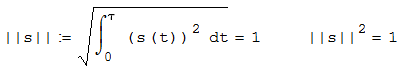 Рисунок 2.19 – Определение нормы и квадрата нормы сигнала s(t) 9. Выражаем в процентной мере относительно квадрата нормы сигнала s(t) квадрат расстояния между сигналами  и s(t) (рисунок 2.20). и s(t) (рисунок 2.20). Рисунок 2.20 – Выражаем в процентной мере относительно квадрата нормы сигнала s(t) квадрат расстояния между сигналами  и s(t) и s(t)Делаем вывод о том, что если верхняя эффективная граничная частота спектра сигнала s(t) fB = 1 кГц, а период дискретизации этого сигнала, найденный в соответствии с теоремой Котельникова, составляет ∆tд = 0,5 мс, то квадрат расстояния между сигналами  и s(t) составляет 41,824% относительно квадрата нормы сигнала s(t). и s(t) составляет 41,824% относительно квадрата нормы сигнала s(t).Исследуем, как изменение верхней эффективной граничной частоты спектра fВ, Гц, сигнала s(t) на квадрат расстояния между сигналами  и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t). Для этого: и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t). Для этого:10. Вновь определим верхнюю эффективную граничную частоту спектра fВ сигнала s(t) на основе энергетического подхода, полагая теперь уже коэффициент уменьшения энергии сигнала по причине искусственного ограничения ширины его спектра k равным 0,95: зададимся начальным приближением параметра fB = 2 кГц (fb:= 2); запишем в блоке Given уравнение относительно искомой граничной частоты спектра fb, полагая коэффициент уменьшения энергии сигнала по причине искусственного ограничения ширины его спектра диапазоном от –fb до fb, равным 0,95 (рисунок 2.21). Приходим к выводу, что первые два лепестка спектральной функции содержит 95% энергии прямоугольного импульса (рисунок 2.22); 11. В соответствии с теоремой Котельникова, вычисляем по формуле (2.2) новую частоту дискретизации fД , кГц, и период дискретизации ∆tд , мс, сигнала s(t) (рисунок 2.23).  Рисунок 2.21 – Повторное определение граничной частоты спектра сигнала s(t).  Рисунок 2.22 – Вновь найденные граничные частоты спектра прямоугольного импульса Рисунок 2.23 – Вычисление новой частоты дискретизации и периода дискретизации сигнала s(t) Как видно из расчетов, приведенных на рисунке 2.23, новая частота дискретизации fД сигнала s(t), удовлетворяющая теореме Котельникова, составляет 4,146 кГц, а период дискретизации ∆tд соответственно равен 0,241 мс; 12. По формуле (2.6) определяем новое количество отсчетов дискретного сигнала (рисунок 2.24). Рисунок 2.24 – Определение нового количества отсчетов дискретного сигнала 13. Формируем вектор дискретных отсчетов {s(k∆  )} (k = 0, 1, 2, ... , 4) непрерывного сигнала s(t)и строим временную диаграмму дискретного сигнала (рисунок 2.25). )} (k = 0, 1, 2, ... , 4) непрерывного сигнала s(t)и строим временную диаграмму дискретного сигнала (рисунок 2.25). Рисунок 2.25 – Вектор дискретных отсчетов и временная диаграмма дискретного сигнала 14. По формуле (2.4) определяем функции {  , составляющие базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его пяти дискретных отсчетов {s(k∆ , составляющие базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его пяти дискретных отсчетов {s(k∆ )} (рисунок 2.26). )} (рисунок 2.26).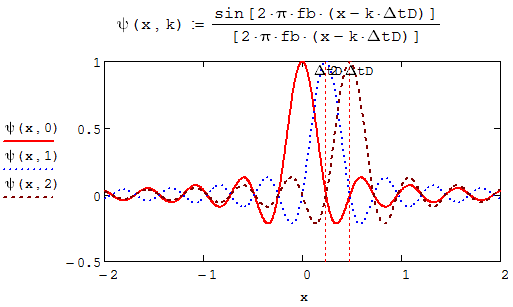 Рисунок 2.26 – Определение функций { 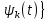 , составляющих базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его пяти дискретных отсчетов {s(k∆ , составляющих базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его пяти дискретных отсчетов {s(k∆ )} )}15. Определяем пять слагаемых, стоящих под знаком суммы в правой части формулы (2.5): произведение k-го дискретного отсчета s(k∆  ) на k-ю базисную функцию ) на k-ю базисную функцию 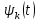 , и результат их суммирования (рисунок 2.27). , и результат их суммирования (рисунок 2.27). Рисунок 2.27 – Определение пяти слагаемых, стоящих под знаком суммы в правой части формулы (2.5) и результата их суммирования 16. По формуле (2.5) определяем функцию  , представляющую результат восстановления исходного непрерывного сигнала s(t) по набору его пяти дискретных отсчетов {s(k∆ , представляющую результат восстановления исходного непрерывного сигнала s(t) по набору его пяти дискретных отсчетов {s(k∆ )}, строим его график и график исходного непрерывного сигнала s(t) (рисунок 2.28). )}, строим его график и график исходного непрерывного сигнала s(t) (рисунок 2.28).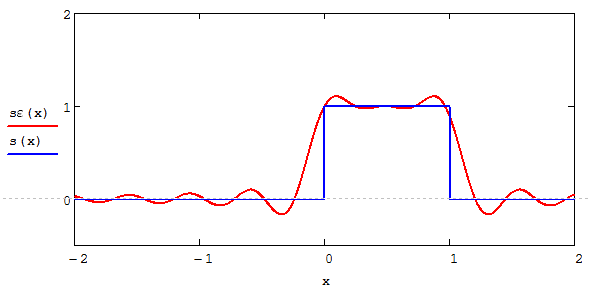 Рисунок 2.28 – Графики функции  и исходного непрерывного сигнала s(t) и исходного непрерывного сигнала s(t) 17. Строим график функции 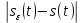 , т. е. погрешности восстановления исходного непрерывного сигнала s(t ) по набору пяти его дискретных отсчетов s(k∆ , т. е. погрешности восстановления исходного непрерывного сигнала s(t ) по набору пяти его дискретных отсчетов s(k∆ ) (рисунок 2.29). ) (рисунок 2.29).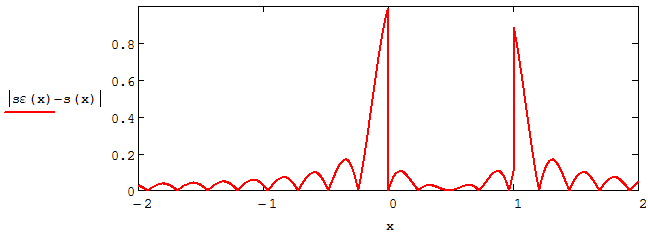 Рисунок 2.29 – График функции  18. По формулам (2.7) и (2.8) определяем расстояние и квадрат расстояния между сигналами  и s(t) (рисунок 2.30). и s(t) (рисунок 2.30).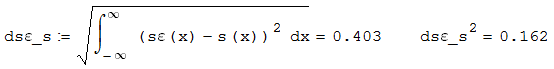 Рисунок 2.30 – Определение расстояния и квадрата расстояния между сигналами  и s(t) и s(t)19. Выражаем в процентной мере относительно квадрата нормы сигнала s(t) квадрат расстояния между сигналами  и s(t) (рисунок 2.31). и s(t) (рисунок 2.31).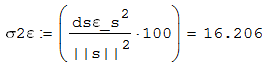 Рисунок 2.31 – Выражаем в процентной мере относительно квадрата нормы сигнала s(t) квадрат расстояния между сигналами  и s(t) и s(t)Делаем вывод о том, что если верхняя эффективная граничная частота спектра сигнала s(t) fB = 2,073 кГц, а период дискретизации этого сигнала, найденный в соответствии с теоремой Котельникова, составляет ∆tд = 0,241мс, то квадрат расстояния между сигналами  и s(t) составляет уже 16,206% относительно квадрата нормы сигнала s(t). Таким образом, по сравнению предыдущим результатом (рисунок 2.20), квадрат расстояния между сигналами и s(t) составляет уже 16,206% относительно квадрата нормы сигнала s(t). Таким образом, по сравнению предыдущим результатом (рисунок 2.20), квадрат расстояния между сигналами  и s(t) уменьшился с 41,824% до 16,206% т. е. 2,581 раза, т. е. качество восстановления сигнала s(t) по набору его дискретных отсчетов s(k∆ и s(t) уменьшился с 41,824% до 16,206% т. е. 2,581 раза, т. е. качество восстановления сигнала s(t) по набору его дискретных отсчетов s(k∆ ) улучшилось. ) улучшилось.Действуя аналогичным образом, было установлено, что: верхняя эффективная граничная частота спектра fВ сигнала s(t), найденная на основе энергетического подхода, при значении коэффициента уменьшения энергии сигнала по причине искусственного ограничения ширины его спектра KE равен 0,99 составляет 10,286 кГц; в соответствии с теоремой Котельникова частота дискретизации сигнала s(t) fД = 20,572 кГц и период дискретизации ∆tд = 0,049 мс; количество отсчетов дискретного сигнала n = 21 ед.; график функции  , представляющей результат восстановления , представляющей результат восстановленияисходного непрерывного сигнала s(t) по набору его 21 дискретного отсчета {s(k∆  )} и график исходного непрерывного сигнала s(t) (рисунок 2.32); )} и график исходного непрерывного сигнала s(t) (рисунок 2.32);график функции 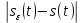 , т. е. погрешности восстановления исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ , т. е. погрешности восстановления исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ )} (рисунок 2.33); )} (рисунок 2.33);расстояние и квадрат расстояния между сигналами  и s(t) (рисунок 2.34); и s(t) (рисунок 2.34);выраженный в процентной мере относительно квадрата нормы сигнала s(t) квадрат расстояния между сигналами  и s(t) (рисунок 2.35). и s(t) (рисунок 2.35). Рисунок 2.32 – Графики восстановленного  по набору его 21-го по набору его 21-годискретного отсчета и исходного непрерывного сигнала s(t) 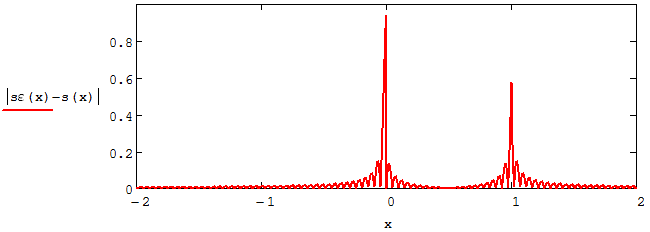 Рисунок 2.33 – График функции 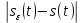 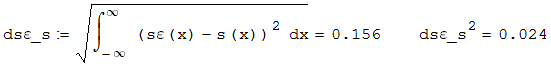 Рисунок 2.34 – Определение расстояния и квадрата расстояния между сигналами  и s(t) и s(t) Рисунок 2.35 – Квадрат расстояния между сигналами  и s(t), и s(t),выраженный в процентной мере относительно квадрата нормы сигнала s(t) Делаем вывод о том, что если верхняя граничная частота спектра сигнала s(t) fB = 10,286 кГц, а период дискретизации этого сигнала, найденный в соответствии с теоремой Котельникова, составляет ∆tд = 0,04965 мс, то квадрат расстояния между сигналами  и s(t) составляет 2,428% относительно квадрата нормы сигнала s(t). и s(t) составляет 2,428% относительно квадрата нормы сигнала s(t).Результаты проведенных исследований оформим в виде таблицы 2.1. Таблица 2.1 – Результаты проведенных исследований 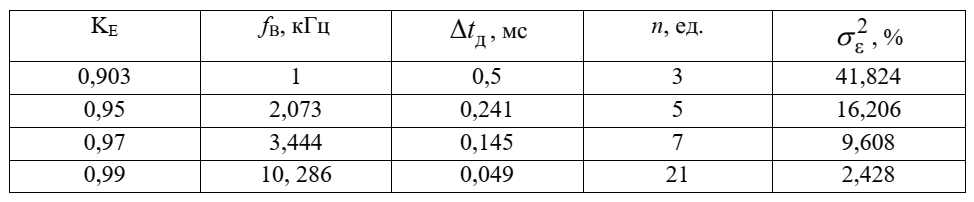 Из данных, представленных в таблице 2.1, делаем вывод о том, что выраженный в процентной мере относительно квадрата нормы сигнала s(t) квадрат расстояния между сигналами  и s(t) менее 10%, если верхняя эффективная граничная частота спектра аналогового сигнала s(t) fB = 10,286 кГц, а период его дискретизации, найденный в соответствии с теоремой Котельникова, составляет ∆tд = 0,049 мс, при этом количество дискретных отсчетов сигнала s(t) равно 21 ед. и s(t) менее 10%, если верхняя эффективная граничная частота спектра аналогового сигнала s(t) fB = 10,286 кГц, а период его дискретизации, найденный в соответствии с теоремой Котельникова, составляет ∆tд = 0,049 мс, при этом количество дискретных отсчетов сигнала s(t) равно 21 ед.Порядок выполнения работы: 13. Запустить Mathcad. 14. Определить в программе Mathcad для заданного непрерывного сигнала s(t) в соответствии с вариантом индивидуального задания (таблица 2.2): верхнюю эффективная граничную частоту спектра fВ, Гц, сигнала s(t), используя энергетический подход; период ∆tд , с, и частоту fД , Гц, дискретизации непрерывного сигнала s(t), удовлетворяющие теореме Котельникова; n – количество отсчетов дискретного сигнала (k = 0, 1, 2, … , n – 1); дискретный сигнал s(k∆  ), полученный в результате дискретизации непрерывного сигнала s(t); ), полученный в результате дискретизации непрерывного сигнала s(t);функции {  , составляющие базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ , составляющие базис Котельникова при восстановлении исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ )} (построить графики для нескольких первых базисных функций, например, для k = 0, 1, 2, ...); )} (построить графики для нескольких первых базисных функций, например, для k = 0, 1, 2, ...);несколько первых слагаемых, стоящих под знаком суммы в правой части формулы (2.5) и представляющих собой произведение k-го дискретного отсчета s(k∆  ) на k-ю базисную функцию ) на k-ю базисную функцию  (построить графики, например, для k = 0, 1, 2, ...); (построить графики, например, для k = 0, 1, 2, ...);функцию  , представляющую результат восстановления исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ , представляющую результат восстановления исходного непрерывного сигнала s(t) по набору его дискретных отсчетов {s(k∆ )} (построить график); )} (построить график);функцию, представляющую модуль разности между  и s(t): и s(t):   (построить график); (построить график);квадрат расстояния между сигналами  и s(t); и s(t);квадрат расстояния между сигналами  и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t). и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t).15. Исследовать, как влияет изменение верхней граничной частоты спектра fВ, Гц, сигнала на квадрат расстояния между сигналами  и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t) и построить соответствующую таблицу, например, по аналогии с таблицей 2.1. и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t) и построить соответствующую таблицу, например, по аналогии с таблицей 2.1.16. Определить, при каких условиях (верхняя эффективная граничная частота спектра fВ сигнала, ∆tд и пр.) квадрат расстояния между сигналами  и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t) не превышает 10%. и s(t), выраженный в процентной мере относительно квадрата нормы сигнала s(t) не превышает 10%.17. Сохранить результаты выполнения индивидуального задания. 18. Сформировать отчет по лабораторной работе. 19. Защитить работу. Варианты заданий Номер варианта соответствует номеру фамилии студента в списке учебной группы (подгруппы). Таблица 2.1 – Варианты индивидуальных заданий  Название, графическое и аналитическое определение параметров исследуемых импульсов приведено в таблице 1.1. Содержание отчета Отчет по лабораторной работе оформляется в виде документа Word и должен включать: 20. Название лабораторной работы. 21. Цель лабораторной работы. 22. Формулировку индивидуального задания и результат его выполнения. 23. Краткие выводы по результатам выполнения лабораторной работы. Контрольные вопросы 24. Какой сигнал называется аналоговым? 25. С какой целью производиться дискретизация аналоговых сигналов? 26. Какой сигнал называется дискретным? 27. Как формулируется теорема В. А. Котельникова? 28. Как восстановить исходный аналоговый сигнал по набору его дискретных отсчетов? 29. Как формируется базис Котельникова? 30. Запишите выражение для k-й базисной функции Котельникова. 31. Каково прикладное значение теоремы В. А. Котельникова для электрической связи? 32. Что такое частота дискретизации аналогового сигнала по Котельникову? 33. Как определить верхнюю граничную частоту спектра сигнала? 34. Как записывается ряд Котельникова, если функция с ограниченным спектром x(t), подлежащая дискретизации, задана на конечном интервале времени T? 35. Как определить конечное число дискретных отсчетов, если функция с ограниченным спектром x(t), подлежащая дискретизации, задана на конечном интервале времени T? 36. Что называется базой сигнала? Чему равнялась база сигнала, исследованного при выполнении индивидуального задания? 37. Чем обусловлена погрешность восстановления сигнала по набору его дискретных отсчетов? 38. Как уменьшить погрешность восстановления сигнала по набору его дискретных отсчетов? 39. Как определить относительную среднеквадратическую погрешность  восстановления исходного непрерывного сигнала x(t) по набору его дискретных отсчетов? восстановления исходного непрерывного сигнала x(t) по набору его дискретных отсчетов?40. Вычислите период дискретизации сигналов: Какое количество отсчетов необходимо для дискретизации этих сигналов? 41. Как может выглядеть аппаратурная реализация синтеза сигнала, представленного рядом Котельникова? 42. Какова методика выполнения индивидуального задания? 43. Какие выводы можно сделать по результатам выполнения индивидуального задания? |
